Теоретическое введение. Определение коэффициента линейного теплового расширения

Определение коэффициента линейного теплового расширения

Цель работы: измерение температурного коэффициента линейного расширения металла.

Для объяснения зависимости теплоемкости твердых тел от температуры (модели Эйнштейна, Дебая) используется модель кристалла, в которой принимается, что отклонения атомов, ионов (частиц, из которых состоит кристалл) из положения равновесия малы по сравнению с расстояниями между ними. Предполагается, что можно точно определить свойства твердого тела, сохраняя в разложении потенциальной энергии кристалла лишь первый неисчезающий член, квадратичный по смещениям атомов. Это – так называемое гармоническое приближение. Предположение о малости колебаний кажется разумным для большинства твердых тел при температурах, лежащих гораздо ниже температуры плавления. Может показаться, что в том случае, когда выполняется предположение о малых колебаниях атомов кристалла, поправки к гармоническому приближению важны лишь в очень точных вычислениях.

Тем не менее ряд свойств твердых тел, проявляющихся при любой температуре, не удается объяснить в чисто гармоническом приближении, поскольку они полностью обусловлены высшими (ангармоническими) членами в разложении энергии взаимодействия атомов вблизи ее равновесного значения. Важнейшее из этих физических свойств – эффект теплового расширения. У строго гармонического кристалла равновесные размеры не зависели бы от температуры.

Для кристаллов с кубической симметрией коэффициент теплового расширения определяется так:

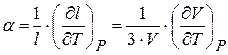. (14.1)

Здесь l – линейные размеры тела, V – его объем. Индекс «P» означает, что производная берется при постоянном давлении.

При свободном тепловом расширении твердого тела тепловая деформация ε (относительное изменение линейных размеров) будет пропорциональна изменению температуры D T:

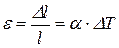. (14.2)

Как правило, с повышением температуры размеры твердых тел увеличиваются, т.е. α>0. Явление теплового расширения в твердых телах обусловлено некоторым изменением характера межатомного взаимодействия при изменении температуры. С усилением теплового движения, с увеличением температуры, с ростом амплитуды колебаний атомов твердого тела силы притяжения и отталкивания между ними, определяющие их энергию взаимодействия, различным образом меняются. И это приводит к тому, что среднее расстояние между атомами в твердом теле изменяется при изменении температуры.

Поясним на простой модели линейной цепочки атомов причины теплового расширения. Для этого рассмотрим влияние ангармонического вклада в выражении для потенциальной энергии взаимодействия пар атомов при температуре T. Потенциальную энергию взаимодействия атомов при смещении на расстояние x от положения равновесия x ₀ представим в виде:

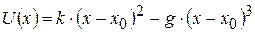. (14.3)

Здесь k – квазиупругая постоянная, g – ангармоническая постоянная; первое слагаемое – потенциальная энергия в гармоническом приближении, второе слагаемое – ангармонический вклад в потенциальную энергию. Он определяет асимметрию взаимного отталкивания атомов. В отсутствие ангармонизма (g =0) на атомы действует только квазиупругая сила – зависимость U (x) описывается параболой. Из (14.3) находим по определению (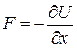) возвращающую силу, действующую на атом:

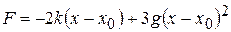. (14.4)

Среднее по времени значение силы (это сила, действующая на атом в состоянии равновесия) должно быть равно нулю, иначе атомы в среднем обладали бы ускорением и сместились из положения равновесия. Так что:

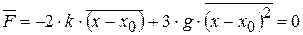. (14.5)

Укажем, что, во-первых, по определению (14.2) 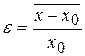, и что в гармоническом приближении (g =0) из (14.5) следует 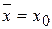, и теплового расширения нет. Этот результат не зависит от амплитуды колебаний атомов. Атомы колеблются гармонически, и в среднем их позиции в кристаллической решётке не зависят от температуры.

Из соотношения (14.5) следует также, что с учётом ангармонизма:

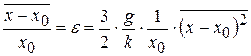. (14.6)

Для нахождения величины 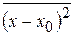можно при высоких температурах воспользоваться классическим законом распределения энергии по степеням свободы:

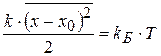, (14.7)

где k_Б – постоянная Больцмана.

Сравнивая (14.6) и (14.2) с учётом (14.7) находим, что для линейной цепочки атомов 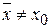, так что отклонения атомов от положения равновесия 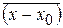становятся зависящими от температуры, а тепловая деформация

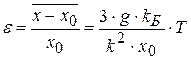, (14.8)

Тогда

. (14.9)

Дата добавления: 2015-03-29