
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретические сведения. В пространстве, окружающем электрические токи и постоянные магниты, возникает силовое поле, называемое магнитным
|
|
|
|
В пространстве, окружающем электрические токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие его обнаруживается по силовому действию на внесенные проводники или постоянные магниты.
Ампер установил, что сила  , с которой магнитное поле действует на элемент проводника
, с которой магнитное поле действует на элемент проводника 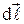 с током прямо пропорциональна силе тока I и векторному произведению элемента
с током прямо пропорциональна силе тока I и векторному произведению элемента 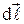 на магнитную индукцию
на магнитную индукцию 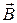 :
:
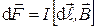 .
.
Модуль силы Ампера вычисляется по формуле
 ,
,
где 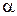 - угол между векторами
- угол между векторами 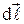 и
и 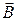 ;
; 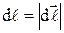 и
и  .
.
Таким образом, вектор магнитной индукции 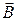 является силовой характеристикой магнитного поля. Последнее изображают с помощью линий магнитной индукции - линий, касательные к которым в каждой точке совпадают с направлением вектора
является силовой характеристикой магнитного поля. Последнее изображают с помощью линий магнитной индукции - линий, касательные к которым в каждой точке совпадают с направлением вектора 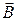 . Магнитная стрелка устанавливается вдоль касательной к линии магнитной индукции, причем ее северный конец N указывает направление вектора
. Магнитная стрелка устанавливается вдоль касательной к линии магнитной индукции, причем ее северный конец N указывает направление вектора 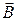 .
.
Закон Ампера позволяет определить единицу измерения магнитной индукции. Пусть элемент проводника 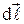 cтоком силой I перпендикулярен линиям магнитной индукции однородного поля. Тогда модуль силы Ампера равен
cтоком силой I перпендикулярен линиям магнитной индукции однородного поля. Тогда модуль силы Ампера равен
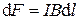 ,
,
при 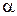 =π/2 и sin
=π/2 и sin 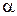 =1.
=1.
Откуда 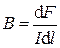 .
.
Единица измерения магнитной индукции - Тесла (Тл).
1 Тесла - магнитная индукция однородного поля, действующего с силой в 1Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно линиям магнитной индукции, если по этому проводнику идет ток силой 1А:
 .
.
Потоком вектора магнитной индукции (магнитным потоком) через площадку d S называется скалярная физическая величина, равная
 ,
,
где В n = В cos 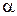 - проекция вектора
- проекция вектора 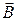 на направление единичного вектора нормали
на направление единичного вектора нормали 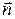 к площадке d S;
к площадке d S; 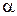 - угол между векторами
- угол между векторами 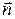 и
и 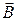 ;
; 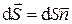 - вектор, модуль которого равен d S (
- вектор, модуль которого равен d S ( ), а направление совпадает с направлением нормали
), а направление совпадает с направлением нормали 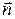 к площадке d S (рис. 1).
к площадке d S (рис. 1).
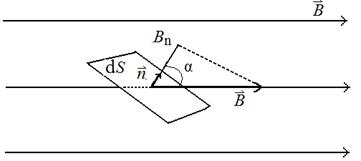
Рис. 1
Для однородного поля и плоской поверхности, перпендикулярной вектору 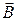 ,
,
В n = В = const и Ф= ВS.
Из последней формулы определяется единица измерения магнитного потока - Вебер (Вб).
1 Вебер -- магнитный поток, проходящий через плоскую поверхность площадью 1м2, перпендикулярную линиям магнитной индукции однородного поля, индукция которого равна 1 Тесле:
1Вб=1Тл 1м2.
Теорема Гаусса для магнитного поля: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю, т.е.
 .
.
Эта теорема отражает отсутствие магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
Электрический ток, идущий по замкнутому контуру, в окружающем пространстве создает магнитное поле, индукция которого, по закону Био-Савара-Лапласа, прямо пропорциональна силе тока. Поэтому магнитный поток Ф пропорционален силе тока I в контуре:
Ф= LI,
где L - коэффициент самоиндукции, или индуктивность контура. Из этого выражения определяется единица измерения индуктивности - Генри (Гн).
1 Генри - индуктивность такого контура, магнитный поток самоиндукции которого при силе тока в 1А равен 1 Веберу:
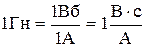
Фарадей открыл закон: при изменении магнитного потока, пронизывающего поверхность, натянутую на замкнутый проводящий контур, в последнем возникает электродвижущая сила (ЭДС) индукции:
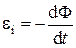
Знак «минус» в этой формуле является математическим выражением правила Ленца: индукционный ток в контуре имеет всегда такое направление, при котором создаваемое им магнитное поле препятствует изменению магнитного потока.
Таким образом, при изменении силы тока в контуре изменяется и сцепленный с ним магнитный поток и, следовательно, индуцируется ЭДС.
Возникновение ЭДС в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Применяя к самоиндукции закон Фарадея, получим, что ЭДС самоиндукции
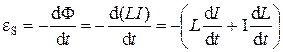 .
.
Если контур не деформируется, то L =const и
 .
.
Значит, на концах катушки возникает ЭДС самоиндукции, препятствующая изменению силы тока.
Определение коэффициента самоиндукции
Рассмотрим электрическую цепь, состоящую из катушки индуктивности L. Катушка имеет активное (омическое) сопротивление R и индуктивное (реактивное) сопротивление ω L, где ω - циклическая частота переменного тока; L - индуктивность катушки. Будем считать, что омическое сопротивление катушки сосредоточено в сопротивлении R, включенном последовательно с ней (рис. 2). На контакты 1 и 2 подается переменное напряжение ~ U с циклической частотой ω.
Пусть в данный момент времени потенциал первого контакта φ1 больше потенциала второго контакта φ2. Тогда ток I идет слева направо.
Допустим, что сила тока I увеличивается, т.е.
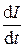 > 0.
> 0.
Тогда, согласно закону Фарадея, на концах катушки L возникает ЭДС самоиндукции, направление которой противоположно направлению тока I в цепи:
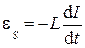 .
.
Если входное напряжение ~ U изменяется по гармоническому закону, то
U = U m cosω t = φ1 - φ2 ,
где U m – амплитуда напряжения.
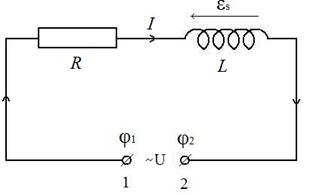
Рис. 2
Запишем закон Ома для этого неоднородного участка цепи:
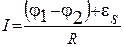 . (1)
. (1)
Тогда 
и 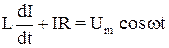 . (2)
. (2)
Частное решение дифференциального уравнения (2) имеет вид
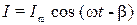 , (3)
, (3)
где I m – амплитуда силы тока; 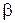 - начальная фаза колебаний тока.
- начальная фаза колебаний тока.
Найдем первую производную:
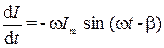 . (4)
. (4)
Выражения (3) и (4) подставим в формулу (2):
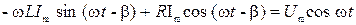 ,
,
 . (5)
. (5)
Пусть 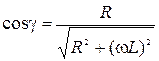 (6)
(6)
и
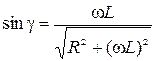 . (7)
. (7)
Подставим выражения (6) и (7) в формулу (5):
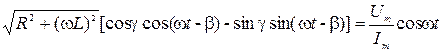 .
.
Отсюда
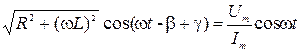 . (8)
. (8)
Равенство (8) будет справедливо для любого момента времени t при условии γ-β=0 и γ=β. Тогда из (8) получаем
 , (9)
, (9)
причем
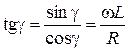 .
.
Из равенства (9) следует, что
 (10)
(10)
является полным электрическим сопротивлением (импедансом) участка цепи, включающим активное сопротивление R и индуктивное сопротивление ω L катушки индуктивности.
На практике с помощью вольтметра и амперметра измеряются эффективные (действующие) значения переменных напряжений и силы тока, связанные с амплитудами следующим образом:
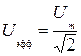 и
и 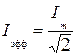 .
.
Значит
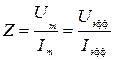 . (11)
. (11)
Из выражения (10) получаем
(ω L)2= Z 2 - R 2
и
 . (12)
. (12)
Следовательно, измеряя полное электрическое сопротивление Z катушки индуктивности при переменном токе и ее омическое сопротивление R при постоянном токе, можно найти индуктивность катушки L.
|
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 524; Нарушение авторских прав?; Мы поможем в написании вашей работы!