Краткие теоретические сведения. Изучение методов построения векторных диаграмм напряжения и токов

Изучение методов построения векторных диаграмм напряжения и токов.

Изучение основных режимов работы электрической цепи при последовательном соединении активно-реактивных элементов.

Определение параметров схемы замещения индуктивной катушки.

Иркутск 2012

Астраханцева Н.М.

Чегаев Н.С.

Лабораторная работа №3

«Исследование режимов работы электрической цепи переменного тока с последовательным соединением катушки индуктивности, резистора и конденсатора»

Выполнил: студент гр. ПСЖ 3-11-4

Принял: доцент кафедры ТОЭ

Цель работы

Определение параметров схемы замещения катушки индуктивности осуществляется путём установления номинального режима при токе I_K= I_2Н = 0,25 А. Установив номинальный режим, снимаются показания приборов: pW₁ – активная мощность, потребляемая катушка индуктивности L₂, Вт; pV­₂ – напряжение на катушке индуктивности, В.

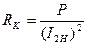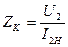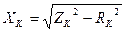, , , (3.1)

где R_K, Z_L=Z_K, X_L=X_K – активное, полное, индуктивное сопротивления катушки L₂, Ом.

Величина ёмкости С₂, при которой в электрической цепи (рис. 4) наступает резонанс напряжения, определяется исходя из условий резонанса напряжения:

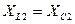, (3.2)

где 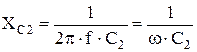, Ом (3.3)

где f – частота, Гц;

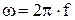– угловая частота, с^-1;

С₂ – ёмкость конденсатора, Ф.

При последовательном соединении резистивного, индуктивного и ёмкостного элементов составляется уравнение напряжения, согласно второму закону Кирхгофа в комплексной форме

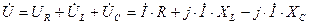(3.4)

где 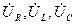– комплексные напряжения на участках цепи;

– комплексный ток в цепи;

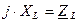– полное комплексное сопротивление индуктивного элемента;

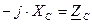– полное комплексное сопротивление ёмкостного элемента.

По закону Ома в комплексной форме определяется ток I, А:

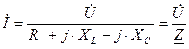, (3.5)

где 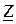– полное комплексное сопротивление электрической цепи.

Пользуясь уравнением второго закона Кирхгофа, можно построить векторную диаграмму. Ток в электрической цепи есть величина постоянная, поэтому за основу построения векторной диаграммы принимаем ток. Векторы напряжений откладываются с учётом характера нагрузки. Вектор напряжения на резистивном элементе совпадает по фазе с вектором тока, на индуктивном элементе опережает на угол 90˚, на ёмкостном – отстаёт на угол 90˚.

Приведём пример построения векторной диаграммы для условия, когда X_L > X_C (рис. 1).

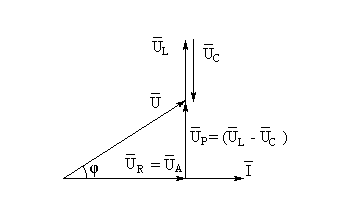
Рис.1 Векторная диаграмма при активно-индуктивно-ёмкостной нагрузке (X_L > X_C)

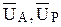– активная и реактивная составляющие напряжения.

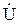Угол φ – угол между векторами тока и напряжения , подводимого к цепи. Если X_L > X_C, то электрическая цепь имеет активно-индуктивный характер, то есть ток отстаёт по фазе от напряжения. Если X_L < X_C, то цепь имеет активно-ёмкостный характер, то есть ток опережает напряжение по фазе.

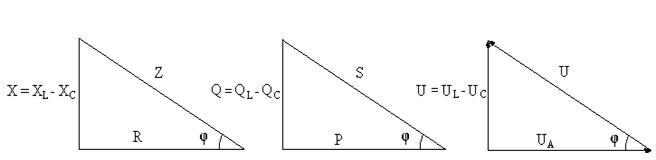
Действующее значение напряжения, приложенного к электрической цепи, можно определить из треугольника напряжений (рис. 2), полученного из векторной диаграммы

а) б) в)

Рис.2 Треугольники: а) сопротивлений; б) мощностей; в) напряжений

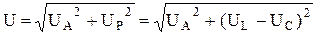. (3.6)

Из треугольника сопротивлений (рис. 2, а):

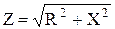. (3.7)

Из треугольника мощностей (рис. 2, б):

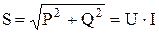, ВА (3.8)

где P – активная мощность электрической цепи вычисляется по формуле

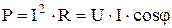, Вт (3.9)

Q – реактивная мощность электрической цепи вычисляется

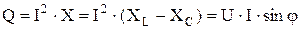, Вар (3.10)

S – полная мощность электрической цепи.

Когда индуктивное сопротивление X_L становится равным ёмкостному сопротивлению X_C (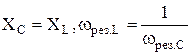), тогда в электрической неразветвлённой цепи наступает резонанс напряжений. Резонансом напряжений называют такой режим работы неразветвлённого участка цепи, содержащий индуктивный, ёмкостный и резистивный элементы последовательного контура, при котором её ток и напряжение совпадают по фазе, то есть φ = 0.

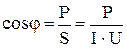. (3.11)

Признаки резонанса напряжения следующие:

1) ток в цепи достигает наибольшего значения

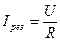, так как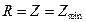

2)

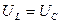
3) полная мощность электрической цепи равна активной, так как реактивная ёмкостная и реактивная индуктивная мощности равны между собой .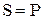

4) 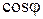становится равным единице ().

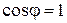Дата добавления: 2015-05-06