
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прогнозирование рынка путем экстраполяции его динамики
|
|
|
|
Экстраполяция — нахождение неизвестного значения динамического ряда за его пределами путем механического переноса тенденций прошлого на будущее. Экстраполяция — наиболее часто используемый и сравнительно простой метод прогнозирования. Для ее применения нужен минимум информации: всего один динамический ряд прогнозируемого показателя, как правило, за 5—7 лет (периодов). Для прогнозирования может быть использована одна из трех разновидностей экстраполяции, причем выбор конкретного способа из этих трех зависит от характера имеющегося динамического ряда. Рассмотрим подробнее применение этих способов на конкретных примерах.
Расчет прогноза по среднему уровню ряда применяется тогда, когда динамический ряд не имеет тенденции роста или снижения и его колебания относительно невелики. В этом случае в качестве прогноза может быть использована средняя арифметическая показателей этого ряда.
Пример 10. Нужно спрогнозировать возможную продажу хлеба в торговой палатке на 7-й день, если его продажа в предыдущие шесть дней характеризуется следующими данными (табл. 8.24):
Таблица 8.24
| Дни (n) | 1-й | 2-й | 3-й | 4-й | 5-й | 6-й |
| Продажа хлеба (y), кг |
Решение. Нетрудно заметить, что данный динамический ряд относительно стабилен и колеблется около средней величины. Расчет проводится по формуле простой средней арифметической:
 кг.
кг.
Полученную величину (1247 кг) можно прогнозировать как объем возможной продажи хлеба на 7-й день. Разумеется, фактическая продажа может несколько отличаться от нашего прогноза, но возможную среднюю ошибку прогноза рассчитывают по формуле
 кг,
кг,
где 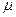 — средняя ошибка прогноза;
— средняя ошибка прогноза;  — дисперсия (
— дисперсия ( ); n — число показателей в динамическом ряду. Такое значение вполне приемлемо, поскольку при краткосрочном прогнозировании допускается средняя ошибка прогноза до 5%, а в нашем случае она составляет лишь 1,6% (20,45: 1247 ∙ 100).
); n — число показателей в динамическом ряду. Такое значение вполне приемлемо, поскольку при краткосрочном прогнозировании допускается средняя ошибка прогноза до 5%, а в нашем случае она составляет лишь 1,6% (20,45: 1247 ∙ 100).
Пример 11. Э кспертам было предложено спрогнозировать объемы продаж зубной щетки «Colgate 360 Супер чистота» в следующем году. В распоряжении экспертов были данные о продажах всех зубных щеток «Колгейт-Палмолив» и условия поставок, а также щеток конкурентов. По данным проведенного экспертного опроса о перспективах продаж зубной щетки «Colgate 360 Супер чистота», составлена таблица 8.25.
Таблица 8.25
Данные экспертного опроса о перспективности объема продаж зубной щетки «Colgate 360 Супер чистота» в городе
| Эксперт | Прогноз объема продаж | Эксперт | Прогноз объема продаж | Эксперт | Прогноз объема продаж |
Для определения оптимального количества групп с равными интервалами – m, воспользуемся формулой Стэрджесса:
 ,
,
где N – число экспертов (30).
Ширина интервала l равна: 
Результаты расчетов представлены в таблице 8.26.
Таблица 8.26
Данные упорядоченного вариационного ряда
| Величина объемов продаж, тыс. руб. | 16-19,2 | 19,2-22,4 | 22,4-25,6 | 25,6-28,8 | 28,8-32 |
| Среднее значение интервала | 17,7 | 20,8 | 27,2 | 30,4 | |
| Количество экспертов, отдавших предпочтение данному варианту |
Средняя величина прогнозируемого объема продаж определится по данным табл. 8.26:  тыс. руб.
тыс. руб.
Рассчитываем характеристику ряда распределения прогнозов экспертов по объему продаж, для этого составим расчетную таблицу 8.27.
Таблица 8.27
Расчетная таблица
| Величина объемов продаж | Количество экспертов
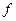
| Середина интервала  
| 
| 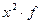
| 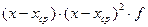
|
| 16-19,2 | 17,7 | 141,6 | 2506,32 | 49,12 | |
| 19,2-22,4 | 20,8 | 124,8 | 2595,84 | 13,74 | |
| 22,4-25,6 | 1,25 | ||||
| 25,6-28,8 | 27,2 | 3699,2 | 68,45 | ||
| 28,8-32 | 30,4 | 182,2 | 5544,96 | 75,66 | |
| ∑ | --------- | 704,8 | 17226,32 | 256,22 |
Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она исчисляется по формуле:
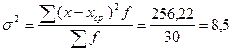 .
.
Среднее квадратическое отклонение равно корню квадратному из дисперсии. Для вариационного ряда: 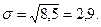
В соответствии с теоремой Чебышева 75% значений признака попадут в интервал 17,7-29,3 тыс. руб., а 89% всех значений попадут в интервал 14,8-32,2 тыс. руб.
2. Прогнозирование по средним темпам роста (снижения) имеет смысл тогда, когда ряду динамики свойственна устойчивая тенденция к повышению или снижению. В этом случае предполагается, что каждый последующий член динамического ряда равен предыдущему, умноженному на средний коэффициент темпов роста (снижения) Iср. Коэффициент исчисляется по формуле
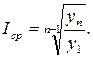
Затем на основе этого коэффициента можно вычислить прогноз по формуле
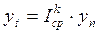
где у1 — начальный показатель ряда; уn — конечный показатель ряда; уt — прогнозируемый показатель; n — количество членов динамического ряда; k — время упреждения прогноза (число прогнозируемых интервалов).
Пример 12. Торговая организация обслуживает 100 тыс. жителей. Требуется рассчитать прогноз возможного объема продажи картофеля в 7-м году, если его продажа в расчете на одного человека за предыдущие пять лет характеризуется данными из таблицы 8.28.
Таблица 8.28
Динамика продаж
| Год | 1-й | 2-й | 3-й | 4-й | 5-й |
| Продажа в расчете на одного человека, кг |
Решение: 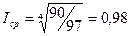 ;
;  кг;
кг;  т.
т.
Таким образом, прогноз возможной продажи картофеля в 7-м году в расчете на одного человека составляет 86,44 кг, а в целом по торговой организации Yt - 8644 т.
Пример 13. Фирма продает чемоданы на роликах. Данные годового объема продаж чемоданов в тыс. руб. представлены в табл. 8.29. Найти средний объем продаж методом скользящей средней и оценить перепады в продажах через индекс сезонности. Составить график маркетинговых мероприятий по стимулированию продаж.
Сущность метода заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3,5,7 и т.д.), первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная с третьего и т.д. Скользящие средние находим по формуле
 ,
,
когда m=(2p-1) – нечетное число; при m=3,p=1, т.е. при t=2 y2=(y1+y2+y3)/3, при t=3 y3=(y2+y3+y4)/3 и т.д. Значение общего среднего уровня можно получить по формуле
 ,
,
где n – количество значений выборки.
Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок. Скользящая средняя представляет собой сглаженный ряд и усредненную закономерность прогнозирования будущей деятельности. Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим. Индексы сезонности определяются по формуле  .
.
Таблица 8.29
Исходные данные и результаты расчета продаж по скользящей средней
| Месяцы года | Объем продаж роликовых чемоданов | Темп роста продаж к предшествующему периоду, % | Трехмесячная скользящая средняя | Индексы сезонности (Iс),% |
| январь февраль март апрель май июнь июль август сентябрь октябрь ноябрь декабрь | - 111,11 146,0 109,58 113,75 142,85 119,23 64,51 78,0 76,92 96,66 138,93 | - (45+50+73)/3=56 (50+73+80)/3=67,67 (73+80+91)/3=81,34 (80+91+130)/=100,3 (91+130+155)/3=125,34 (130+155+100)/3=128,34 (155+100+78)/3=111 (100+78+60)/3=79,34 (78+60+58)/3=65,34 (60+58+80)/3=66 - | - 56/88,07=64 100,65 | |
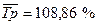
|  88,07 88,07
| 95,9 |
Прогноз объема продаж на январь месяц следующего года =  88,07∙108,86/100 = 95,87 тыс. руб.
88,07∙108,86/100 = 95,87 тыс. руб.
Совокупность исчисленных для каждого интервала времени индексов сезонности характеризует сезонную волну развития изучения явления в динамике. На рис. 8.8 показан график сезонности (по месяцам) продаж чемоданов для примера из табл. 8.29.
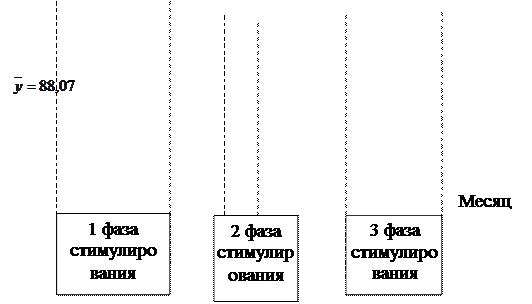
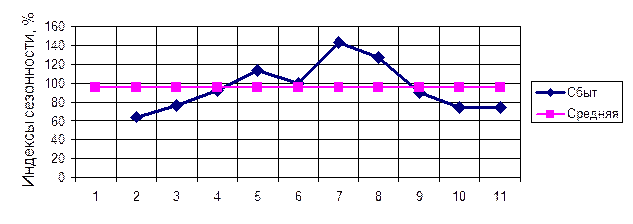
Рис. 8.8. Характеристика сезонной волны продаж на примере роликовых чемоданов
Характеристика функции сбыта объясняется сезоном отдыха и путешествий. Исходя из графика продаж (рис. 8.8) фирма выделяет 3 фазы проведения кампании по стимулированию (табл. 8.30).
Таблица 8.30
План-график проведения мероприятий по стимулированию
| Фаза 1 | Фаза 2 | Фаза 3 |
| С 15 февраля по 15 мая | С 10 июня по 10 июля | С 15 ноября по 31 декабря |
Пример 14. Необходимо осуществить прогнозирование объема продаж товаров и услуг компьютерного магазина «Железо» методом экстраполяции. На основании анализа бухгалтерской отчетности составим таблицу 8.31 объема продаж.
Таблица 8.31
Исходные данные по динамике продаж
| Кварталы года | I | II | III | IV |
| Выручка тыс. руб. |
1). Определим среднегодовой объем выручки за отчетный период:
 тыс. руб.
тыс. руб.
2). Найдем абсолютное изменение объема выручки, тыс. руб. Абсолютный прирост рассчитывается как разность между двумя уровнями ряда. В зависимости от базы сравнения абсолютные приросты могут рассчитываться как цепные и как базисные.
Цепные показатели, то есть по отношению к предыдущему кварталу:

Базисные, то есть по отношению к отчетному кварталу:
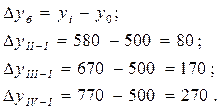
3). Вычислим темпы роста, в %. Темп роста показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение.
а) цепные по формуле 
КII-I = 580 /500*100 = 116; КIII-II = 670 /580*100 = 115; КIV-III = 770 /670 *100 = 115.
б) базисные по формуле 
KII-I = 580 / 500 *100 = 116; KIII-I = 670 / 500*100 = 134; KIV = 770 / 500*100 = 154.
4). Вычислим темпы прироста (сокращения), в %. Темп прироста показывает на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения: Тпр = Тр –100;
а) цепные: TII-I = 116 – 100 = 16; TIII-II = 115 – 100 = 15; TIV-III = 115 – 100 = 15.
б) базисные: TII-I = 116 – 100 = 16; TIII-I = 134 – 100 = 34; TIV-I = 154 – 100 = 54.
Произведенные математические расчеты по динамике вариационных рядов сведем в таблицу 8.32.
5). Средний абсолютный прирост составит в тыс. руб.:
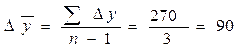 ,
,
то есть в среднем за период времени с 1го по 4ый кварталы объем выручки увеличился на 90 тыс. руб.
6). Средний темп роста, в %
 .
.
Таким образом, за период времени с 1го по 4ый кварталы года объем выручки ежеквартально увеличивался на 115,3%.
Таблица 8.32
Исходные данные и математические расчеты по динамике вариационных рядов
| Квартал | Выручка тыс. руб. | Абсолютные изменения объема выручки, тыс. руб. | Темпы роста, в % | Темпы прироста, в % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| I | - | - | - | - | - | - | |
| II | |||||||
| III | |||||||
| IV |
7). Прогноз выручки на I-й и II-й кварталы следующего года:
На основе среднего абсолютного прироста: 
YI = 770 + 90 = 860 тыс. руб.; YII = 860 + 90 = 950 тыс. руб.
На основе среднего темпа роста: 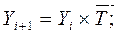
YI = 770*1,153 = 887,81 тыс. руб.; YII = 887,81*1,153 = 1023,6 тыс. руб.
8). Прогноз на II и III кварталы будущего года по методу скользящей средней:

3. Выравнивание (сглаживание) динамического ряда.
Этот способ экстраполяции также применяется при наличии устойчивой тенденции роста или снижения. Тенденция развития прогнозируемого явления приблизительно описывается графиком какого-либо математического уравнения, а затем на основе подобранного уравнения рассчитывается прогноз.
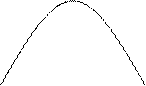
В схематическом виде данный метод представлен на рис. 8.9. В зависимости от характера динамического ряда на практике для прогнозных расчетов применяются различные математические функции. Наиболее часто используемые функции и соответствующие им графики показаны на рис. 8.10.
  |
Рис. 8.9. Прогнозирование развития рынка методом экстраполяции



 y y y
y y y
 |






 t t t
t t t



 y y y
y y y
 | |||
 | |||
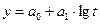


 t t t
t t t
Рис. 8.10.Графики математических функций, описывающих тенденции развития спроса
Выравнивание по скользящей средней. Сущность метода заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3,5,7 и т.д.), первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная с третьего и т.д.
Скользящие средние находим по формуле
 ,
,
когда m=(2p-1) – нечетное число; при m=3,p=1, т.е. при t=2 y2=(y1+y2+y3)/3, при t=3 y3=(y2+y3+y4)/3 и т.д. Значение общего среднего уровня можно получить по формуле
 ,
,
где n – количество значений выборки.
Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок. Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим.
Пример 15. Н еобходимо рассчитать средний темп роста регионального рынка рекламы и прогноз его линейного роста на следующий год исходя из таблицы 8.33.
Таблица 8.33
Исходные данные рекламного рынка
| Годы | Объем рекламного рынка города, млн. руб. | Темп роста рекламного рынка к предшествующему периоду, % | Средний темп роста рекламы за 5 лет, % |
| - 108,57 110,52 114,28 116,66 | 112,51 |
Прогноз объема рекламного рынка (2012 г.) = Объем рекламы (2010 г.)*(средний темп роста / 100) = 280(112,51/100)=. 315,03 млн. руб.
Вместе с тем, с помощью этого метода трудно прогнозировать период менее 3-5 лет, поскольку слишком мала выборка, массив обрабатываемой статистической информации, а также период проявления действия циклических колебаний.
Пример 16. Рассмотрим тенденцию сбытовой деятельности предприятия по данным табл. 8.34.
Таблица 8.34
Исходные данные и результаты расчета скользящей-средней
| Месяцы года | Объем сбытовой деятельности, тыс. $ | Трехмесячная скользящая средняя | Индексы сезонности (Iс) |
| - (85+70+83)/3=79,3 (70+83+80)/3=77,6 (83+80+75)/3=79,33 (80+75+78)/=77,66 (75+78+82)/3=78,33 (78+82+71)/3=77 (82+71+78)/3=77 (71+78+80)/3=76,33 - | - 79,3/77,82=101,90 99,71 101,94 99,79 100,65 98,94 98,94 98,08 | ||
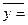 77,82 77,82
| 99,99 |
Таким образом, скользящая средняя представляет собой сглаженный ряд и усредненную закономерность прогнозирования будущей деятельности.
Индексы сезонности определяются по формуле
Iс = 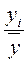 100%.
100%.
Совокупность исчисленных для каждого интервала времени индексов сезонности характеризует сезонную волну развития изучения явления в динамике. На рис. 8.11 показан график сезонности для примера из табл. 8.34.
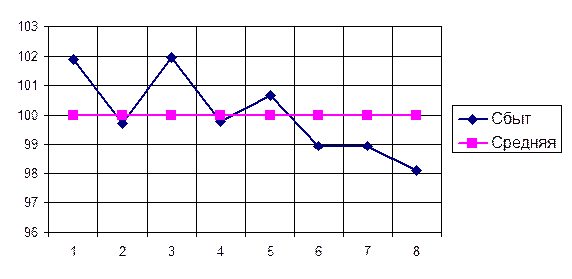
Рис. 8.11. Сезонная волна сбытовой деятельности
Выравнивание по прямой используется, как правило, в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии или близко к ней.
Простейшей моделью, выражающей тенденции развития является линейная функция тренда. Рассмотрим построение линии тренда по прямой
y = a0 + a1t,
где t – порядковый номер периода или момента времени; а1 – коэффициент регрессии, определяющий направление развития тренда. Если а>0, то уровни ряда динамики равномерно возрастают, а при а<0 происходит их равномерное снижение. Этому типу динамики присущи постоянные приросты:  Рассмотрим линейный прогноз развития на основании данных табл. 8.35.
Рассмотрим линейный прогноз развития на основании данных табл. 8.35.
Таблица 8.35
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 5342; Нарушение авторских прав?; Мы поможем в написании вашей работы!