Дайте определение уравнения Бернулли. Приведите пример

Дайте определение и приведите пример автономного дифференциального уравнения. Сформулируйте свойство решений автономного уравнения.

Одним из важных частных случаев дифференциальных уравнений с разделяющимися переменными являются так называемые автономные уравнения. Это уравнения вида:y’=g(y).

Замечание: Если у*- корень уравнения g(y)=0, то у=у* (у-const) является решением уравнения y’=g(y). Такое решение называется стационарным.

Теорема: Если у=фи(х) – решение автономного дифференциального уравнения, то у=фи(х+С) также является решением этого уравнения.

Пример: y’=cos(2y+2x+6). Делая замену z=2y+2x+6, находим z’=2y’+2. Следовательно, z’=2cosz+2, или z’=4cos²z/2.

Дифференциальное уравнение вида y’+p(x)y=f(x)yⁿ (n≠0, n≠1) называется уравнением Бернулли. Пример: y’-y=e^6x/y². Решение: n=-2. Выполним замену z=y³, получим z’=3y²y’. Далее решаем полученное уравнение: z’-3z=3e^6x

18. Дайте определение и приведите пример линейного дифференциального уравнения второго порядка. Докажите, что есл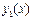и и – решения линейного неоднородного уравнения, то разность является решением соответствующего линейного однородного уравнения

Линейным уравнением второго порядка называется уравнение y”+p(x)y’+q(x)y=b(x). Пример y”+5y’+6y=4sin(x).

Т.к. Y1(X) и Y2(X) явл решением, то: Y’+p(X)Y=G(X) - верное по усл

Y1’(X)+P(X)Y1(X)=G(X)-верное по усл

Y2’+P(X)Y2(X)=G(x)- верное по усл

Y1’(X)-Y2’(X)+P(X)(Y1(X)-Y2(X)))=0 –это и есть решение.

19. Дайте определения системы линейно зависимых и системы линейно независимых функций. Установить линейную независимость системы функций , , .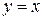

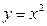Функции y₁(x), y₂(x),..., y_n(x), определённые на отрезке [a;b], называются линейно зависимыми на [a;b], если существуют постоянные α₁, α₂,..., α _n, не равные нулю одновременно и такие, что α₁y₁(x) + α₂y₂(x) +... + α _n y _n (x) = 0 для всех x из отрезка [a;b].

В противном случае функции y₁(x), y₂(x),..., y_n(x) называются линейно независимыми.

Линейную зависимость и линейную независимость функций определяют также на (a;b), (a;b], [a;b), на бесконечных промежутках.

Справедливо следующее утверждение.

Функции y₁(x), y₂(x),..., y_n(x) линейно зависимы на отрезке [a;b] тогда и только тогда, когда хотя бы одна из них является линейной комбинацией других на этом отрезке.

20. Установить линейную зависимость системы функций 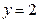, , . Пусть функции линейно независимы, тогда составим определитель Вронского:

Данные функции линейно зависимы так первую функцию можно представить в виде линейной комбинации двух других 2= 1*(x+1)+(-1)+(x-1), соответственно можно подобрать такие α1,α2,α3 при которых верно равенство: α1*y1+α2*y2+α3*y3=0

1*(x+1)+(-1)*(x-1)+(-1)*2=0

21. Докажите, что сумма частного решения линейного неоднородного дифференциального уравнения второго порядка и общего решения соответствующего однородного уравнения является общим решением линейного неоднородного уравнения второго порядка. Общее решение неоднородного уравнения L(y)=f(x)есть сумма частного решения ‾у(х) этого уравнения и общего решения соответствующего ему однородного уравнения L(y)=0. Доказательство: Покажем сначала, что сумма у(х) частного решения уравнения неоднородного уравнения ‾у(х)и произвольного решения у₀(х) однородного уравнения также является решением неоднородного уравнения. Действительно, в силу леммы имеем L(‾y+y₀)=L(‾y)+L(y₀)=f(x)+0=f(x), что и требовалось доказать. Теперь нам осталось доказать, что всякое решение у(х) неоднородного уравнения есть сумма ‾у(х) и некоторого частного решения у₀(х) уравнения L(y)=f(x). Имеем L(у-‾y)=L(y)-L(‾y)=f(x)-f(x)=0.Следовательно, у₀(х)=у(х)-‾у(х) – решение уравнения L(y)=0, значит, у(х)=у₀(х)+‾у(х), что и завершает доказательство.

Возьмем ур-е (1): . Решением ур-я(1) будет сумма частного и общего решения однородного ур-я .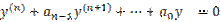

Док-во. Тогда имеем *: 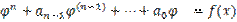. Возьмем любое решение ур-я (1)**: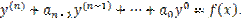

Вычтем их ** уравнение *, получим: ЧТД

22. Докажите, что линейная комбинация решений линейного однородного дифференциального уравнения второго порядка также является решением этого уравнения. Пусть у₁(х) и у₂(х),….,у_к(х) – произвольные решения линейного однородного дифференциального уравнения и С₁, С₂,….,С_к – произвольные постоянные, тогда линейная комбинация С₁у₁(х)+С₂у₂(х)+….+С_ку_к(х) также является решением этого уравнения. Действительно, на основании L(C₁y₁+C₂y₂)= C₁L(y₁)+C₂L(y₂), имеем: L(C₁y₁+C₂y₂+….+C_ky_k)=C₁L(y₁)+C₂L(y₂)+…+C_kL(y_k)=0 что и требовалось доказать.

Дата добавления: 2015-03-29