Собственные числа, характеристический полином, присоединенная матрица

Некоторые сведения из теории матриц

Решение неоднородных векторно-матричных дифференциальных уравнений

Ранее были получены выражения для определения решений однородного дифференциального уравнения нестационарной

(2.3.5)

и стационарной

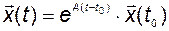(2.3.14)

систем. Используем эти результаты для определения решения неоднородного линейного векторно-матричного уравнения, соответствующего (2.2.7):

. (2.3.16)

Произведем замену:

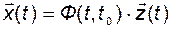(2.3.17)

и продифференцируем это выражение:

.

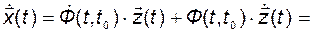
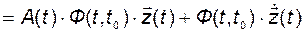Сопоставляя это выражение с предыдущим, получим

,

откуда

,

или, интегрируя,

.

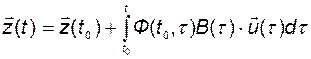Из (2.3.17) видно, что

.

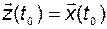В итоге получаем выражение для решения векторно-матричного линейного неоднородного дифферен­циального уравнения, известное под названием формулы Коши:

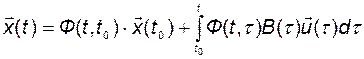. (2.3.18)

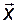Умножение квадратной матрицы на некоторый вектор дает новый вектор 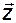, который, в общем случае, иначе ориентирован в про­странстве и имеет другую длину по сравнению с исходным вектором. Однако существуют и такие векторы, которые при выполнении этой опе­рации меняют только свою длину, но не меняют направления, то есть

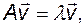(2.4.1)

где 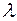- вещественная или комплексная скалярная величина, назы­ваемая собственным значением (характеристическим числом) матрицы , а вектор - собственный вектор этой матрицы. В развёрну­том виде уравнение (2.4.1) имеет следующий вид:

.

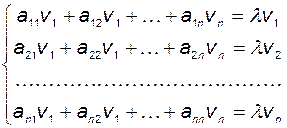Очевидно, что для существования ненулевых необходимо вы­пол­не­ние условия

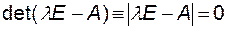. (2.4.2)

Это уравнение называют характеристическим, или вековым уравнением матрицы . Левая часть этого уравнения называется характеристичес­ким полиномом, степень его равна размеру n матрицы :

. (2.4.3)

Таким образом, каждая квадратная матрица имеет 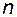собственных зна­чений , которые могут быть определены путём решения характеристического уравнения с использованием стандартного матема­тического обеспечения на цифровых вычислительных машинах.

Алгебраическая кратность корня 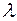– это его кратность как корня характеристического уравнения. Геометрическая кратность корня 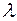– это количество линейно независимых векторов 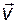, связанных с данным .

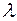Если 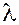не является собственным значением матрицы , то существует матрица 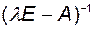. По правилу определения обратных матриц

, (2.4.4)

где - присоединённая матрица для матрицы . Ее элементы определяются как алгебраические дополнения элементов матрицы 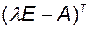. Здесь символ Т означает транспонирование. Присоединённая матрица - это матричный полином степени n-1:

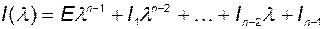, (2.4.5)

где – единичная матрица .

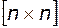Если все собственные числа матрицы различны, то собственные векторы матрицы могут быть выбраны пропорциональными любым ненулевым столбцам матрицы .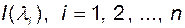

ПРИМЕР 2.4.1. Пусть объект задан структурной схемой, приведённой на рис.2.8.

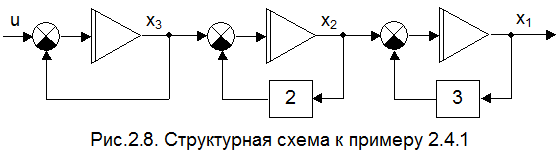
Ему соответствует система уравнений

;

;

,

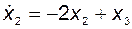или в матричном виде

,

где

; .

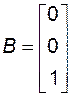Для этих исходных данных получаем характеристический полином

.

Ему соответствуют собственные числа

Найдем присоединенную матрицу

=

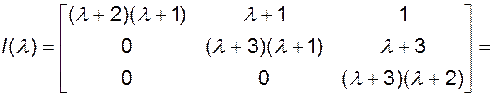
Найдём собственные векторы матрицы :

и можно выбрать

.

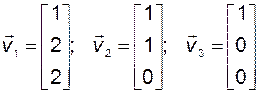Полученный результат нетрудно проверить прямой подстановкой в (2.4.1).

Имеется ряд алгоритмов для определения коэффициентов характеристического полинома и присоединенной матрицы. Один из наиболее употребимых - это алгоритм Фаддеева - Леверье. Он состоит в следующей последовательности вычислений:

A₁=A; a_=- ; I₁=A₁+a_E;

A₂=AI₁; 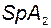; I₂=A₂+a_E;

..........................................

A_n-1=AI_n-2; ; I_n-1=A_n-1+a_E;

A_n=AI_n-1; 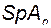; I_n=A_n+ _E=0.

Здесь через обозначен след матрицы , то есть сумма ее диагональных элементов

.

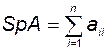Последнее равенство процедуры используется для контроля точности вычислений.

Для объекта, приведенного в примере 2.4.1,

.

Если матрица не вырожденна, то из промежуточных результатов алгоритма Фаддеева - Леверье, учитывая, что

получаем

. (2.4.6)

Для рассматриваемого примера

.

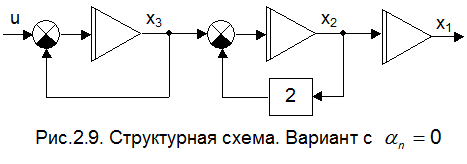
В вырожденном случае . Иллюстрацией этого может служить объект, структурная схема которого приведена на рис.2.9.

Дата добавления: 2015-03-31