Синтез архитектуры наблюдателя

Наблюдатель Люенбергера полного порядка

Рассмотрим линейную стационарную систему, которая описывается векторно-матричными дифференциальными уравнениями:

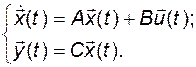(3.11.1)

Для такой системы существуют алгоритмы модального синтеза, которые позволяют найти управление

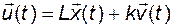, (3.11.2)

обеспе­чивающее заданные динамику и статику системы. Проблема заключается в необходимости использования вектора обратной связи для формирова­ния такого управления. Фактически в распоряжении разработчика системы управления лишь вектор выхода . Возникает вопрос: как, наблюдая за вектором , восстановить вектор 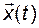или найти его оценку 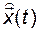? При этом ошибка оценки вектора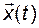

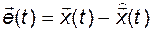(3.11.3)

должна быть относительно малой и тем более с течением времени не должна расти.

Будем полагать, что разработчику достаточно хорошо известны параметры объекта, то есть оценки матриц . Более того, положим

. (3.11.4)

В этом случае, если построить аналоговую или цифровую модель объекта в соответствии с уравнениями

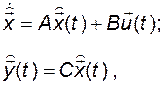(3.11.5)

как показано на рис. 3.16, то можно было бы ожидать выполнения равенств

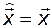и 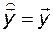. (3.11.6)

Однако априорное знание объекта (в том числе матриц , 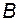и ) является приближённым, параметры его могут дрейфовать во времени, начальные условия для вектора состояния, которые следовало бы подставить в модель, неизвестны. Поэтому в действительности в такой схеме ошибка оценки вектора состояния может иметь склонность к неограниченному росту с течением времени.

Американским учёным Д.Г.Люенбергером впервые были изучены структуры работоспособных асимптотических идентификаторов (наблюдателей, восстановителей) вектора состояния, названных позднее его именем. Основополагающая идея состоит в том, чтобы в рассмотренную структурную схему ввести дополнительную обратную связь по ошибке оценки вектора , заведомо обеспечивающую асимптотическое затухание ошибки оценки вектора состояния. Внешне структурная схема наблюдателя Люенбергера полного порядка, которая приведена на рис. 3.17, совпадает с одной из форм известного фильтра Калмана. Различие в том, что матрица , которая в фильтре Калмана называется его именем (матрицей Калмана), в наблюдателе Люенбергера рассчитывается из других соображений.

В соответствии с рис.3.17 уравнение наблюдателя будет иметь вид

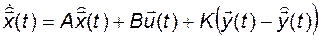. (3.11.7)

Получим уравнение для ошибки оценки вектора состояния. Для этого в равенство (3.11.3) подставим выражения для вектора состояния и его оценки из (3.11.1) и (3.11.7):

,

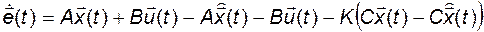откуда

, (3.11.8)

где

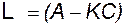(3.11.9)

называют матрицей динамики наблюдателя. Выражение (3.11.8) является однородным дифференциальным уравнением. Решение его имеет вид

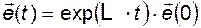. (3.11.10)

Поведение ошибки во времени зависит от собственных чисел матрицы наблюдателя 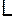. Выбрав их соответствующим образом, можно достаточно быстро свести ошибку к нулю и получать от наблюдателя точную оценку вектора состояния. Далее будет показано, что если пара 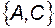наблюдаема, то соот­вет­ствующим выбором матрицы K можно обеспечить любое желаемое рас­положение собственных чисел наблюдателя, т.е. матрицы 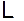. Практически собственные значения наблюдателя выбираются так, чтобы состояние наблюдателя 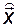сходилось к состоянию наблюдаемой системы несколько быстрее затухания пере­ходных процессов в желаемой замк­нутой системе. Чрезмерное ускорение наблюдателя приводит к затру­днениям при его реализации.

3.11.1.2. Алгоритм определения матрицы К для систем
со скалярным выходом

Если пара наблюдаема, то в пространстве вектора состояния существует базис 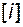, в котором эта пара имеет идентификационное ка­ноническое представление (ИКП) .

Обозначим некоторый исходный базис как 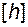. В этом базисе дифференциальное уравнение для ошибки оценки вектора состояния имеет вид

. (3.11.11)

Перейдём к базису ИКП. Используем уже известное соотношение, связывающее координатные столбцы одного и того же вектора в разных базисах:

. (3.11.12)

Используя эту подстановку, запишем

.

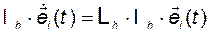Умножив обе части последнего равенства на 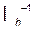, получим

,

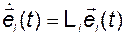где

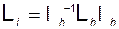. (3.11.13)

Кроме того,

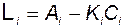, (3.11.14)

где

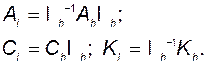(3.11.15)

Матрица динамики наблюдателя в базисе ИКП в соответствии с уравнением (3.11.4) имеет вид

,

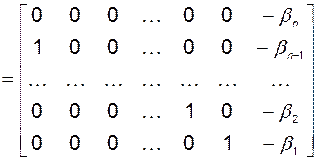где – коэффициенты характеристического полинома наблюдателя, которые вычисляются на основании желаемых собственных чисел наблюдателя 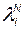согласно выражению

. (3.11.16)

Очевидно выражение для элементов матрицы в базисе ИКП:

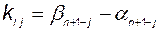, . (3.11.17)

Перевод матрицы в исходный или какой-либо другой базис может быть произведён в соответствии с выражением (3.11.15).

ПРИМЕР 3.11.1. Построить наблюдатель полного порядка для объекта со структурной схемой, приведённой на рис. 3.18.

Запишем матрицы объекта в исходном базисе:

, , .

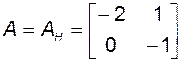Характеристический полином объекта (матрицы динамики )

,

его коэффициенты

,

нули (собственные числа)

.

Время переходного процесса в объекте определяется наиболее близким к мнимой оси собственным числом :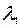

.

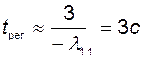Зададим собственные числа наблюдателя

.

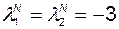Им соответствует характеристический полином наблюдателя

,

его коэффициенты

.

В соответствии с (3.11.17) определяем элементы матрицы и саму эту матрицу в базисе ИКП:

.

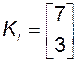Для того чтобы перевести матрицу в исходный базис, рассчитаем матрицу наблюдаемости и обратную ей в исходном базисе:

; ;

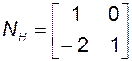учитывая представление в базисе ИКП

; ,

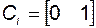рассчитаем в этом базисе матрицу наблюдаемости

.

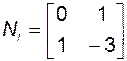В соответствии с (3.11.13) вычислим матрицу перехода от исходного базиса 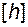к базису ИКП :

.

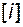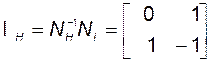Используя (3.11.15), получим матрицу в исходном базисе

.

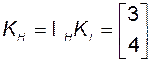Теперь можно заняться уравнением наблюдателя в исходном базисе. В соответствии с (3.11.9) имеем

.

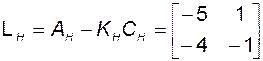Учитывая (3.11.17), запишем, опуская далее индекс исходного базиса:

. (3.11.18)

Тогда уравнение наблюдателя будет иметь вид

.

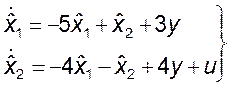Дата добавления: 2015-03-31