Методы решения задач квадратичного программирования

Применение условия Куна-Таккера для решения З.К.П.

Постановка задачи:

min f(x) =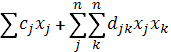

Ограничения:

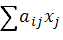≤ b_i, i = 1 ÷ m

x_j ≥ 0, j = 1 ÷ n

Составим функцию Лагранжа:

L (x, d) =

Условия Куна-Таккера:

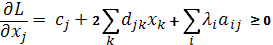
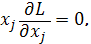
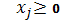
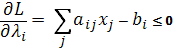
Преобразуем полученную систему таким образом, чтобы линейные неравенства стали равенствами.

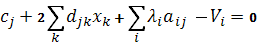
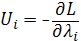
Таким образом, задача свелась к решению системы линейных уравнений с учетом дополнительных нелинейных ограничений.

Дополнительные ограничения означают, что переменные (x_j и V_j) или (λ_i и U_i) не могут однозначно бысть отличны от 0, т.е. не могут одновременно присутствовать в базисе.

Система линейных равенств может быть решена с помощью симплекс-преобразований.

Метод Билла для решения З.К.П.

Является обобщением симплекс-метода и применяется для решения З.К.П.

Постановка задачи:

min f(x) =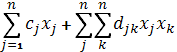

Ограничения:

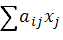= b_i, i = 1 ÷ m

x_j ≥ 0, j = 1 ÷ n

Равенство и переменные неотрицательны.

Будем предполагать, что данная задача является задачей выпуклого программирования (f (x) – выпуклая вниз).

Алгоритм:

1) Найти исходное опорное решение (с помощью симплекс-преобразований).

Предположим, что систему ограничений удалось разрешить, относительно базисных переменных x₁…x_m, тогда x_m+1…x_n – свободные.

x_i = b_i + , i = 1 ÷ m,

b_i ≥ 0, i = 1 ÷ m

Выразим функции f(x) через свободные переменные

f(x) =c₀+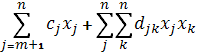

1 решение:

x_n+1=…=x_n=0

x_j=b_j, j=1 ÷ m

f₁(x)= c₀

2) Проверка найденного решения на оптимальность.

Для проверки решения на оптимальность вычисляются частные производные от функции f(x) по всем свободным переменны в найденной точке.

Согласно условиям Куна-Таккера, найденное решение будет оптимальным, если все частные производные , j=(m+1)÷n

Если найдется хотя бы одна производная отрицательная, то за счет введения свободной переменной в базис решение можно улучшить.

Предположим, что частная производная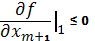

Переменную x_m+1 будем вводить в базис.

3) Переход к новому опорному решению.

Случай № 1

Предположим, что при увеличении переменной x_m+1, первой в 0 обращается базисная переменная, например x_1.

Тогда из выражения x₁= b₁+ 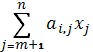найдем переменную x_m+1= b_m+1+a_(m+1),1x₁+ 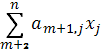и подставим полученное выражение в уравнение для всех базисных переменных и целевую функцию.

2 решение:

x₁=x_m+2=…=x_n=0

x­_i=b_i, i=2÷(m+1)

f₂(x)=c₀

Найденное решение необходимо проверить на оптимальность.

Случай № 2

Пусть при увеличении x_m+1 первой в 0 обращается производная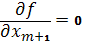

Введем дополнительную переменную U₁= 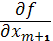и из полученного выражения найдем x_m+1

Полученное выражение подставим в уравнение для всех базисных переменных и в целевую функцию.

Получим

U₁= x₁=x_m+2=…=x_n=0

x_i=b_i, i=1÷(m+1)

f₂(x) = c₀

Найденное решение необходимо проверить на оптимальность.

Замечания:

1) Переменная U₁ является неограниченной по знаку, поэтому условие оптимальности по этим переменным имеют вид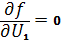

2) Если при выполнении очередной итерации U₁ стала базисной, то ее можно исключить из дальнейших рассуждений.

Поэтому, проверяя решение на оптимальность, в первую очередь проверяется условие оптимальности по переменной U₁

3) Задача max f(x)

Условие оптимальности 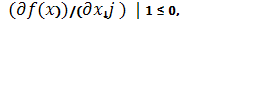j=(m+1) ÷n

Если найдется хотя бы одна положительная производная, например 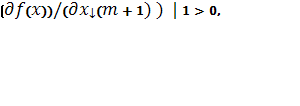то найденное решение можно улучшить, за счет ввода переменной х_m+1 в базис.

Если при вводе х_m+1 в базис имеем Случай № 2, то дополнительная переменная U₁ =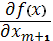

Дата добавления: 2015-04-23