Методы решения задач динамического программирования

1) Метод прямого хода

2) Метод обратного хода

Процесс нахождения решения разбивается на 2 стадии условную и безусловную оптимизацию.

На этапе условной оптимизации для каждого шага определяется условное оптимальное управление и условный оптимальный выигрыш, на всех шагах начиная с данного и до последнего включительно, в методе обратной прогонки, или с 1го до данного включительно в методе прямой прогонки.

На этапе безусловной оптимизации для каждого шага находится безусловное оптимальное управление и max значение W. Безусловная оптимизация в методе обратной прогонки идет от 1го шага к последнему.

В методе прямой прогонки наоборот условная от 1 к последнему, безусловная от последнего к первому.

3) Метод обратной прогонки

При нахождении управления на каждом шаге нельзя исходить из интересов шага в отдельности. Необходимо исходить из всего процесса в целом.

Принцип оптимальности Беллмана:

Какого бы ни было состояние системы к очередному шагу, управление на этом шаге нужно выбирать так, чтобы сумма выигрыша на этом шаге и оптимальна на всех последующих шагах была max.

W_i(S_i-1) – условный оптимальный выигрыш на всех шагах от i до n при условии, что к i шагу состояние системы будет S_i-1.

U_i^* - условное оптимальное управление на i шаге, который совместно с оптимальным управлением на всех последующих шагах достигал max W(S_i-1).

Рассмотрим i-шаг.

Предположим, что за предыдущий (i-1)-шаг система пришла в состояние S_i-1.

Выберем произвольное управление U_i на i-шаге.

В результате этого управления на i-шаге будет получен выигрыш f_i(S_i-1, U_i).

Кроме того, система перейдет в новое состояние S_i, которое представляет собой функцию S_i = φ(S_i-1, U_i) – уравнение состояний.

Оптимальный выигрыш на всех последующих шагах при условии, что к (i+1)-шагу состояние системы будет S_i составит W_i+1(S_i).

Сумма выигрыша на i-шаге и оптимум на всех последующих шагах будет = f_i(S_i-1, U_i)+W_i+1(S_i).

Согласно принципу Беллмана, управление U_i нужно выбрать так, чтобы полученная сумма была maх, то управление, при котором достигается max этой суммы и будет являться условным оптимальным управлением на этом шаге, т.е. U_i^*.

Max этой суммы достигает условный оптимальный выигрыш на всех последующих шагах, начиная с i до n – включительно, при условии, что к i-шагу состояние было S_i-1.

W_i(S_i-1) = max {f_i(S_i-1,U_i) + W_i+1(S_i)} – основная функция управления.

Отдельно функция управления записывается для последнего шага

W_n(S_n-1) = max {f_n(S_n-1,U_n)}

Max берется по всем управлениям U_n, которые приводят систему S в S_n = φ(S_n-1, U_n) 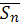℮ на этапе условной оптимизации необходимо найти W_n(S_n-1), U_n^*, W_n-1(S_n-2), U_n-1^*…W₁(S₀), U^*.

Безусловная оптимизация.

S₀ – задано

W₁(S₀) = W_max

S₀ ℮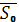

W_max = max W₁(S₀)=W₁(S₀^*)

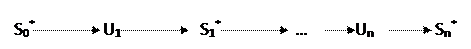S_n 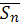℮ – множество конечных состояний

Таким образом, для построения модели динамического программирования, а так же для решения необходимо выполнить следующее.

1) Выбрать способ деления процесса управления на шаги

2) Для каждого шага определить U_i и параметры состояний системы S_i

3) Записать уравнение состояний S_i= φ(S_i-1, U_i)

4) Для i-шага записать выигрыш, соответствующий выбранному управлению U_i

5) Записать функцию управления

W_i(S_i-1) = max {f_i(S_i-1,U_i) + W_i+1(S_i)}

W_n(S_n-1) = max {f_n(S_n-1,U_n)}

6) Провести условную оптимизацию

W_n(S_n-1), U_n^*, W_n-1(S_n-2), U_n-1^*…W₁(S₀), U^*.

7) Провести безусловную оптимизацию

4) Метод прямой прогонки

Уравнение состояний

S_i-1 = φ(S_i, U_i)

Функциональное уравнение:

Z_i(S_i) = max f_i(S_i, U_i)+Z_i-1(S_i-1)

Z_i(S_i) – условный оптимальный выигрыш на всех шагах с 1 по i-й включительно

Условная оптимизация от 1 шага к последнему, безусловная – от последнего к 1-му.

5) Венгерский алгоритм

В основе метода 2 утверждения:

1) Если решение x_ij является оптимальным решением для задачи о назначениях, то оно является оптимальным и для задач с функциями

f’=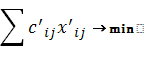

c’_ij=c_ij - V_j – U_i (V и U – некоторые константы)

Ограничения вспомогательной задачи совпадают с ограничениями исходной.

2) Если функции f’= 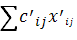, с_ij ≥ 0 и можно найти такой набор значений переменных x_ij, для которых сумма =0, то это решение является оптимальным.

Таким образом, метод сводится к добавлению и вычитанию констант к строкам или столбцам, до тех пор, пока количество коэффициентов c’_ij, а именно n не станут = 0, что и даст оптимальное решение поставленной задачи.

Дата добавления: 2015-04-23