Основные методы экологических исследований 7 страница

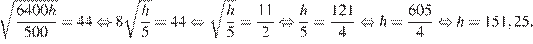
Сле­до­ва­тель­но, чтобы ви­деть го­ри­зонт на более да­ле­ком рас­сто­я­нии, на­блю­да­те­лю нужно под­нять­ся на 151,25 − 11,25 = 140 мет­ров. Для этого ему не­об­хо­ди­мо под­нять­ся на 140: 0,2 = 700 сту­пе­нек.

Ответ: 700.

13. B 13. В пра­виль­ной ше­сти­уголь­ной приз­ме 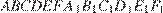все ребра равны 1. Най­ди­те тан­генс угла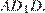

Ре­ше­ние.

Рас­смот­рим пря­мо­уголь­ный тре­уголь­ник 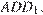катет ко­то­ро­го яв­ля­ет­ся боль­шей диа­го­на­лью ос­но­ва­ния. Длина боль­шей диа­го­на­ли пра­виль­но­го ше­сти­уголь­ни­ка равна его удво­ен­ной сто­ро­не: . По­сколь­ку 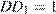имеем:

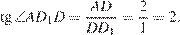
Ответ: 2.

Из пунк­та A кру­го­вой трас­сы вы­ехал ве­ло­си­пе­дист, а через 10 минут сле­дом за ним от­пра­вил­ся мо­то­цик­лист. Через 2 ми­ну­ты после от­прав­ле­ния он до­гнал ве­ло­си­пе­ди­ста в пер­вый раз, а еще через 3 ми­ну­ты после этого до­гнал его во вто­рой раз. Най­ди­те ско­рость мо­то­цик­ли­ста, если длина трас­сы равна 5 км. Ответ дайте в км/ч.

Ре­ше­ние.

До пер­вой встре­чи ве­ло­си­пе­дист про­вел на трас­се 1/5 часа, а мо­то­цик­лист 1/30 часа. Пусть ско­рость мо­то­цик­ли­ста равна км/ч, тогда ско­рость ве­ло­си­пе­ди­ста равна

.

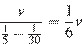Еще через 1/20 часа после пер­вой встре­чи, мо­то­цик­лист до­гнал ве­ло­си­пе­ди­ста во вто­рой раз. Имеем:

Таким об­ра­зом, ско­рость мо­то­цик­ли­ста была равна 120 км/ч.

Ответ: 120.

При­ве­дем ариф­ме­ти­че­ское ре­ше­ние ре­ше­ние.

За­ме­тим, что к мо­мен­ту пер­вой встре­чи мо­то­цик­лист за 2 ми­ну­ты про­ехал столь­ко же, сколь­ко ве­ло­си­пе­дист за 12 минут. Сле­до­ва­тель­но, ско­рость мо­то­цик­ли­ста в 6 раз боль­ше ско­ро­сти ве­ло­си­пе­ди­ста. Это озна­ча­ет, что от мо­мен­та пер­вой встре­чи до мо­мен­та вто­рой мо­то­цик­лист, дви­га­ясь по кругу, до­го­ня­ет ве­ло­си­пе­ди­ста со ско­ро­стью сбли­же­ния, рав­ной пяти ско­ро­стям ве­ло­си­пе­ди­ста. При этом пре­одо­ле­ва­ет раз­де­ля­ю­щее их рас­сто­я­ние 5 км за три ми­ну­ты. Тогда ско­рость сбли­же­ния со­став­ля­ет 1 км за три ми­ну­ты или 20 км в час, а ско­рость мо­то­цик­ли­ста равна 120 км в час.

15. B 15. Най­ди­те наи­боль­шее зна­че­ние функ­ции на от­рез­ке .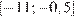

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

.

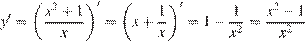Про­из­вод­ная об­ра­ща­ет­ся в нуль в точ­ках 1 и −1, за­дан­но­му от­рез­ку при­над­ле­жит толь­ко число −1. Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции на за­дан­ном от­рез­ке:

Наи­боль­шим зна­че­ни­ем функ­ции на за­дан­ном от­рез­ке будет . Най­дем его:

.

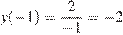Ответ: −2.

16. C 1. Ре­ши­те урав­не­ние 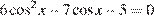. Ука­жи­те его корни, при­над­ле­жа­щие от­рез­ку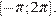

Ре­ше­ние.

Сде­ла­ем за­ме­ну 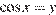, по­лу­чим квад­рат­ное урав­не­ние 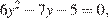кор­ня­ми ко­то­ро­го яв­ля­ют­ся числа и Урав­не­ние 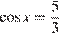не имеет ре­ше­ний, а из урав­не­ния 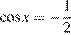на­хо­дим ис­ко­мые корни:

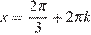или ; .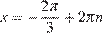

Най­дем корни, при­над­ле­жа­щие от­рез­ку 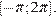Решим не­ра­вен­ства:

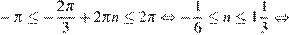
или ;

Со­от­вет­ству­ю­щие най­ден­ным зна­че­ни­ям па­ра­мет­ров корн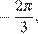и: и .

Ответ: . За­дан­но­му от­рез­ку при­над­ле­жат корни и .

17. C 2. В кубе 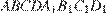все ребра равны 1. Най­ди­те рас­сто­я­ние от точки до пря­мой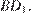

Ре­ше­ние.

Про­ве­дем от­ре­зок и опу­стим пер­пен­ди­ку­ляр на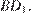

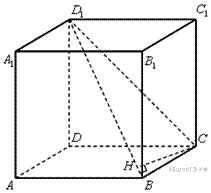
Ис­ко­мое рас­сто­я­ние равно вы­со­те пря­мо­уголь­но­го тре­уголь­ни­ка 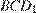с пря­мым углом

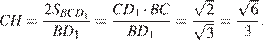
Ответ: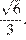

18. C 3. Ре­ши­те не­ра­вен­ство .

Ре­ше­ние.

Не­ра­вен­ство имеет смысл при

.

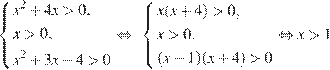Для таких х по­лу­ча­ем

.

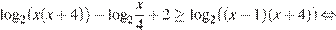
Зна­чит, .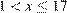

Ответ: .

19. C 4. Че­ты­рех­уголь­ник опи­сан около окруж­но­сти и впи­сан в дру­гую окруж­ность. Пря­мые 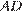и 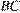пе­ре­се­ка­ют­ся в точке 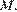Най­ди­те пе­ри­метр тре­уголь­ни­ка 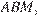если из­вест­но, что 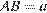и

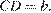
Ре­ше­ние.

Воз­мож­ны два слу­чая 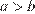и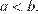

Пер­вый слу­чай. Че­ты­рех­уголь­ник опи­сан около окруж­но­сти, сле­до­ва­тель­но, 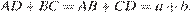Че­ты­рех­уголь­ник впи­сан в окруж­ность, зна­чит, 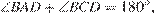но 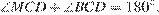от­ку­да сле­до­ва­тель­но, с ко­эф­фи­ци­ен­том по­до­бия

Обо­зна­чим через 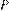пе­ри­метр тре­уголь­ни­ка тогда если 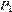— пе­ри­метр тре­уголь­ни­ка

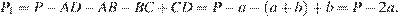
По­сколь­ку 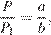по­лу­ча­ем: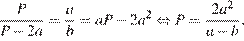

Вто­рой слу­чай. Ана­ло­гич­но слу­чаю 1 имеем:

Ответ: 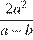или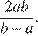

20. C 5. При каких зна­че­ни­ях па­ра­мет­ра а си­сте­ма 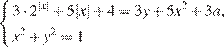имеет един­ствен­ное ре­ше­ние?

Ре­ше­ние.

Пре­жде всего: за­ме­тим, что если 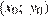— ре­ше­ние си­сте­мы при не­ко­то­ром зна­че­нии па­ра­мет­ра а, то при этом зна­че­нии па­ра­мет­ра ре­ше­ни­ем си­сте­мы будет и 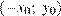. От­сю­да сле­ду­ет, что усло­вие яв­ля­ет­ся не­об­хо­ди­мым усло­ви­ем су­ще­ство­ва­ния у си­сте­мы един­ствен­но­го ре­ше­ния.

При си­сте­ма пе­ре­пи­шет­ся в виде

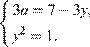
Решая эту си­сте­му от­но­си­тель­но а, на­хо­дим, что тре­бу­е­мые зна­че­ния а могут при­над­ле­жать толь­ко мно­же­ству 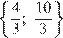. Пусть . Тогда си­сте­ма при­мет вид

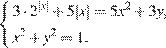
Из вто­ро­го урав­не­ния си­сте­мы сле­ду­ет, что и 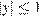, и, таким об­ра­зом, 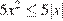. Учи­ты­вая те­перь, что , при­хо­дим к не­ра­вен­ству

,

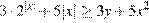ко­то­рое озна­ча­ет, что пер­вое ра­вен­ство си­сте­мы спра­вед­ли­во толь­ко при 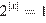, , 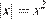сле­до­ва­тель­но, , т. е. при , . Итак, при си­сте­ма имеет един­ствен­ное ре­ше­ние.

Пусть те­перь . При таком зна­че­нии па­ра­мет­ра а си­сте­ма пе­ре­пи­шет­ся в виде

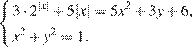
Эта си­сте­ма имеет ре­ше­ния , , 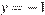, 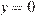и, таким об­ра­зом, при усло­вию един­ствен­но­сти ре­ше­ния не удо­вле­тво­ря­ет. За­ме­тим, что ре­ше­ния здесь про­сто уга­да­ны.

Ответ: .

21. C 6. За­ду­ма­но не­сколь­ко (не обя­за­тель­но раз­лич­ных) на­ту­раль­ных чисел. Эти числа и их все воз­мож­ные суммы (по 2, по 3 и т. д.) вы­пи­сы­ва­ют на доску в по­ряд­ке не­убы­ва­ния. Если какое-то число n, вы­пи­сан­ное на доску, по­вто­ря­ет­ся не­сколь­ко раз, то на доске остав­ля­ет­ся одно такое число n, а осталь­ные числа, рав­ные n, сти­ра­ют­ся. На­при­мер, если за­ду­ма­ны числа 1, 3, 3, 4, то на доске будет за­пи­сан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.

а) При­ве­ди­те при­мер за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 1, 2, 3, 4, 5, 6, 7.

б) Су­ще­ству­ет ли при­мер таких за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 20, 22?

в) При­ве­ди­те все при­ме­ры за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 7, 9, 11, 14, 16, 18, 20, 21, 23, 25, 27, 30, 32, 34, 41.

Ре­ше­ние.

а) За­ду­ман­ные числа 1, 1, 1, 1, 1, 1, 1 дают тре­бу­е­мый набор, за­пи­сан­ный на доске.

б) По­сколь­ку за­ду­ман­ные числа на­ту­раль­ные, то наи­мень­шее число в на­бо­ре — это наи­мень­шее из за­ду­ман­ных чисел, а наи­боль­шее число в на­бо­ре — это сумма всех за­ду­ман­ных чисел. Среди чисел за­пи­сан­но­го на­бо­ра долж­на быть сумма всех чисел, кроме наи­мень­ше­го, то есть 22 − 1 = 21. Но этого числа нет в на­бо­ре, по­это­му не су­ще­ству­ет при­ме­ра таких за­ду­ман­ных чисел, для ко­то­ро­го на доске будет вы­пи­сан набор из усло­вия.

в) Число 7 — наи­мень­шее число в на­бо­ре — яв­ля­ет­ся наи­мень­шим из за­ду­ман­ных чисел, а наи­боль­шее число в на­бо­ре — это сумма всех за­ду­ман­ных чисел. По­это­му ко­ли­че­ство за­ду­ман­ных чисел не пре­вос­хо­дит целой части 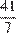, то есть 5. Кроме того, числа 9 и 11 мень­ше, чем сумма двух чисел 7, по­это­му они также яв­ля­ют­ся за­ду­ман­ны­ми. Зна­чит, сумма остав­ших­ся за­ду­ман­ных чисел равна 41 − 7 − 9 − 11 = 14. Таким об­ра­зом, так как наи­мень­шее за­ду­ман­ное число равно 7, остав­ши­е­ся за­ду­ман­ные числа — это 7 и 7 или 14. Для за­ду­ман­ных чисел 7, 7, 7, 9, 11 и 7, 9, 11, 14 на доске будет за­пи­сан набор, дан­ный в усло­вии.

Ответ: а) 1, 1, 1, 1, 1, 1, 1; б) нет; в) 7, 7, 7, 9, 11 или 7, 9, 11, 14.

ОТВЕТЫ Вариант № 11

1. B 1. Шо­ко­лад­ка стоит 35 руб­лей. В вос­кре­се­нье в су­пер­мар­ке­те дей­ству­ет спе­ци­аль­ное пред­ло­же­ние: за­пла­тив за две шо­ко­лад­ки, по­ку­па­тель по­лу­ча­ет три (одну в по­да­рок). Сколь­ко шо­ко­ла­док можно по­лу­чить на 200 руб­лей в вос­кре­се­нье?

Ре­ше­ние.

Раз­де­лим 200 на 35:

.

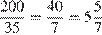Зна­чит, можно будет ку­пить 5 шо­ко­ла­док. Еще 2 будут даны в по­да­рок. Всего можно будет по­лу­чить 7 шо­ко­ла­док.

Ответ: 7.

2. B 2. 1 ки­ло­ватт-час элек­тро­энер­гии стоит 1 рубль 80 ко­пе­ек. Счет­чик элек­тро­энер­гии 1 но­яб­ря по­ка­зы­вал 12 625 ки­ло­ватт-часов, а 1 де­каб­ря по­ка­зы­вал 12 802 ки­ло­ватт-часа. Сколь­ко руб­лей нужно за­пла­тить за элек­тро­энер­гию за но­ябрь?

Ре­ше­ние.

Рас­ход элек­тро­энер­гии за но­ябрь со­став­ля­ет 12 802 − 12 625 = 177 ки­ло­ватт-часов. Зна­чит, за но­ябрь нужно за­пла­тить 1,8 177 = 318,6 рубля.

Ответ: 318,6.

3. B 3. На гра­фи­ке изоб­ра­же­на за­ви­си­мость кру­тя­ще­го мо­мен­та ав­то­мо­биль­но­го дви­га­те­ля от числа его обо­ро­тов в ми­ну­ту. На оси абс­цисс от­кла­ды­ва­ет­ся число обо­ро­тов в ми­ну­ту. На оси ор­ди­нат — кру­тя­щий мо­мент в Н м. Чтобы ав­то­мо­биль начал дви­же­ние, кру­тя­щий мо­мент дол­жен быть не менее 60 Н м. Какое наи­мень­шее число обо­ро­тов дви­га­те­ля в ми­ну­ту до­ста­точ­но, чтобы ав­то­мо­биль начал дви­же­ние?

Ре­ше­ние.

Из гра­фи­ка видно, что кру­тя­щий мо­мент 60 Н м до­сти­га­ет­ся при 2000 обо­ро­тов дви­га­те­ля в ми­ну­ту (см. ри­су­нок).

Ответ: 2000.

В сред­нем граж­да­нин А. в днев­ное время рас­хо­ду­ет 125 кВт ч элек­тро­энер­гии в месяц, а в ноч­ное время — 155 кВт ч элек­тро­энер­гии. Рань­ше у А. в квар­ти­ре был уста­нов­лен од­но­та­риф­ный счет­чик, и всю элек­тро­энер­гию он опла­чи­вал по та­ри­фу 2,6 руб. за кВт ч. Год назад А. уста­но­вил двух­та­риф­ный счeтчик, при этом днев­ной рас­ход элек­тро­энер­гии опла­чи­ва­ет­ся по та­ри­фу 2,6 руб. за кВт ч, а ноч­ной рас­ход опла­чи­ва­ет­ся по та­ри­фу 0,7 руб. за кВт ч. В те­че­ние 12 ме­ся­цев режим по­треб­ле­ния и та­ри­фы опла­ты элек­тро­энер­гии не ме­ня­лись. На сколь­ко боль­ше за­пла­тил бы А. за этот пе­ри­од, если бы не по­ме­нял­ся счет­чик? Ответ дайте в руб­лях.

Ре­ше­ние.

Рас­смот­рим оба типа счётчи­ков.

При ис­поль­зо­ва­нии од­но­та­риф­но­го счётчика, граж­да­нин А. пла­тил в месяц

(125 кВт ч + 155 кВт ч) 2,6 руб. за 1 кВт ч = 728 руб.

По­это­му за 12 ме­ся­цев он пла­тил 728 1 2 = 8736 руб.

При ис­поль­зо­ва­нии двух­та­риф­но­го счётчика, граж­да­нин А. пла­тит в месяц

125 кВт ч 2,6 руб. + 155 кВт ч 0,7 руб. = 433,5 руб.

По­это­му за 12 ме­ся­цев он за­пла­тит 433,5 руб. 12 = 5202 руб.

Уста­нов­ка но­во­го типа счётчика поз­во­ля­ет эко­но­мить 8736 руб. − 5202 руб. = 3534 руб. в год.

5. B 5. Бо­ко­вые сто­ро­ны тра­пе­ции, опи­сан­ной около окруж­но­сти, равны 3 и 5. Най­ди­те сред­нюю линию тра­пе­ции.

Ре­ше­ние.

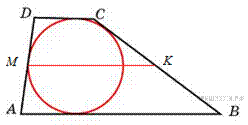
в вы­пук­лый че­ты­рех­уголь­ник можно впи­сать окруж­ность тогда и толь­ко тогда, когда

Ответ: 4.

6. B 6. В слу­чай­ном экс­пе­ри­мен­те бро­са­ют две иг­раль­ные кости. Най­ди­те ве­ро­ят­ность того, что в сумме вы­па­дет 8 очков. Ре­зуль­тат округ­ли­те до сотых.

Ре­ше­ние.

Ко­ли­че­ство ис­хо­дов, при ко­то­рых в ре­зуль­та­те брос­ка иг­раль­ных ко­стей вы­па­дет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каж­дый из ку­би­ков может вы­пасть ше­стью ва­ри­ан­та­ми, по­это­му общее число ис­хо­дов равно 6·6 = 36. Сле­до­ва­тель­но, ве­ро­ят­ность того, что в сумме вы­па­дет 8 очков, равна

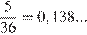
Ответ: 0,14.

Ре­ши­те урав­не­ние 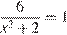. Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

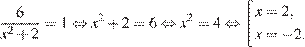
Ответ: 2.

8. B 8. 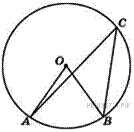Цен­траль­ный угол на 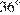боль­ше остро­го впи­сан­но­го угла, опи­ра­ю­ще­го­ся на ту же дугу окруж­но­сти. Най­ди­те впи­сан­ный угол. Ответ дайте в гра­ду­сах.

Ре­ше­ние.

Впи­сан­ный угол равен по­ло­ви­не цен­траль­но­го угла, опи­ра­ю­ще­го­ся на ту же дугу окруж­но­сти, зна­чит

Ответ: 36.

9. B 9. На ри­сун­ке изоб­ражён гра­фик функ­ции y = F (x) — одной из пер­во­об­раз­ных не­ко­то­рой функ­ции f (x), опре­делённой на ин­тер­ва­ле (−3;5). Поль­зу­ясь ри­сун­ком, опре­де­ли­те ко­ли­че­ство ре­ше­ний урав­не­ния f (x)=0 на от­рез­ке [−2;4].

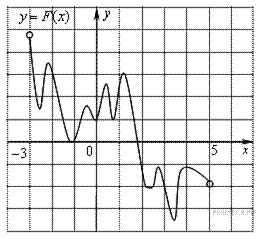
Ре­ше­ние.

По опре­де­ле­нию пер­во­об­раз­ной на ин­тер­ва­ле (−3; 5) спра­вед­ли­во ра­вен­ство

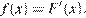
Сле­до­ва­тель­но, ре­ше­ни­я­ми урав­не­ния f (x)=0 яв­ля­ют­ся точки экс­тре­му­мов изоб­ра­жен­ной на ри­сун­ке функ­ции F (x) Это точки −2,6; −2,2; −1,2; −0,5; 0; 0,4; 0,8; 1,2; 2,2; 2,8; 3,4; 3,8. Из них на от­рез­ке [−2;4] лежат 10 точек. Таким об­ра­зом, на от­рез­ке [−2;4] урав­не­ние 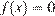имеет 10 ре­ше­ний.

Ответ:10.

10. B 10. 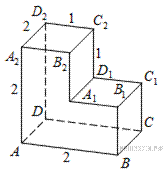Най­ди­те угол 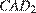мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Ответ дайте в гра­ду­сах.

Ре­ше­ние.

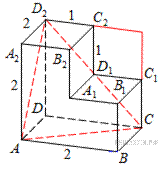Рас­смот­рим тре­уголь­ник 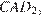где т. к. яв­ля­ют­ся диа­го­на­ля­ми рав­ных квад­ра­тов. Сле­до­ва­тель­но, тре­уголь­ник 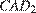– рав­но­сто­рон­ний, по­это­му все его углы равны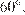

Ответ: 60.

11. B 11. Най­ди­те зна­че­ние вы­ра­же­ния .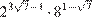

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

.

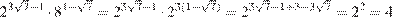Ответ: 4.

12. B 12. На­хо­дя­щий­ся в воде во­до­лаз­ный ко­ло­кол, со­дер­жа­щий молей воз­ду­ха при дав­ле­нии ат­мо­сфе­ры, мед­лен­но опус­ка­ют на дно водоeма. При этом про­ис­хо­дит изо­тер­ми­че­ское сжа­тие воз­ду­ха. Ра­бо­та, со­вер­ша­е­мая водой при сжа­тии воз­ду­ха, опре­де­ля­ет­ся вы­ра­же­ни­ем 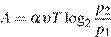(Дж), где — по­сто­ян­ная, К — тем­пе­ра­ту­ра воз­ду­ха, (атм) — на­чаль­ное дав­ле­ние, а 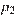(атм) — ко­неч­ное дав­ле­ние воз­ду­ха в ко­ло­ко­ле. До ка­ко­го наи­боль­ше­го дав­ле­ния 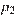можно сжать воз­дух в ко­ло­ко­ле, если при сжа­тии воз­ду­ха со­вер­ша­ет­ся ра­бо­та не более чем 29 100 Дж? Ответ при­ве­ди­те в ат­мо­сфе­рах.

Ре­ше­ние.

За­да­ча сво­дит­ся к ре­ше­нию не­ра­вен­ства 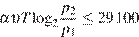при за­дан­ных зна­че­ни­ях по­сто­ян­ной , тем­пе­ра­ту­ры воз­ду­ха К, на­чаль­но­го дав­ле­ния атм и ко­ли­че­ства воз­ду­ха моль:

Дата добавления: 2015-04-23