Решение. Построить таблицу истинности для заданной логической схемы (логическая схема должна содержать не менее трех входов)

Пример

Построить таблицу истинности для заданной логической схемы (логическая схема должна содержать не менее трех входов).

Pascal

QBasic

Написать и отладить программу обработки вещественных данных.

Пример. Написать и отладить программу приближенного нахождения корня уравнения e^x - 3x =0 на отрезке [1; 5] методом половинного деления с точностью 0,01.

Решение. Решение задачи состоит из двух частей — отделение корня и уточнение корня.

Отделение корня можно реализовать программно или с помощью вспомогательных программных средств (например, с помощью MS Excel). Рассмотрим второй вариант отделения корня (напомним, что на некотором отрезке существует корень, если функция на этом отрезке меняет знак; если она к тому же монотонна, то корень единственный). Протабулируем левую часть уравнения на заданном отрезке с шагом 0,1.

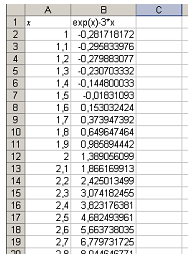
Замечаем, что рассматриваемая функция на заданном отрезке [1; 5] меняет знак лишь единожды на отрезке [1,5; 1,6]. На этом отрезке и будем уточнять корень.

DECLARE FUNCTION F! (x!)

PRINT "Введите a, b, eps:"

INPUT a, b, eps

DO

c = (a + b) / 2

IF F(a) * F(c) < 0 THEN b = c ELSE a = c

LOOP UNTIL b — a < eps

x = (a + b) / 2

PRINT USING "###.######"; x

FUNCTION F (x)

F = EXP(x) — 3 * x

END FUNCTION

program divide_half;

var a,b,c,eps,x:real;

function f(x:real):real;

begin f:= exp(x) - 3*x end;

begin

write('Введите a, b, eps: ');

readln(a, b, eps);

repeat

c:= (a + b)/2;

if f(a) * f(c) < 0 then b:= c

else a:= c

until b – a < eps;

x:= (a + b)/2;

writeln('x=', x:10:7)

end.

C++

#include <iostream.h>

#include <math.h>

double f(double x);

void main()

{ double a,b,c,eps,x;

cout << "Введите a, b, eps:";

cin >> a >> b >> eps;

do

{ c = (a + b)/2;

if (f(a) * f(c) < 0) b = c; else a = c;

} while (b – a >= eps);

x = (a + b)/2;

cout << x;

}

double f(double x)

{

return exp(x) – 3 * x;

}

Задания

На отрезке [–10; 10] (или на той его части, что входит в область определения уравнения) отделите корни. Уточните один из корней по методу половинного деления с точностью e с помощью программы для компьютера.

Уравнения:

1) x – 10sin x = 0

Контроль

1-й корень [-8.43;-8.42]

x = -8.42320393239788

2-й корень [-7.07;-7.06]

x = -7.06817435807170

3-й корень [-2.86;-2.85]

x = -2.85234189447510

4-й корень [-0.01; 0.00]

x = 0.00000000002053

5-й корень [ 2.85; 2.86]

x = 2.85234189443872

6-й корень [ 7.06; 7.07]

x = 7.06817435810808

7-й корень [ 8.42; 8.43]

x = 8.42320393235423

2) x sin x – 1 = 0

Контроль (для отрезка [–10; 10])

1-й корень [-9.32;-9.31]

x = -9.31724294142623

2-й корень [-6.44;-6.43]

x = -6.43911723842757

3-й корень [-2.78;-2.77]

x = -2.77260470826150

4-й корень [-1.12;-1.11]

x = -1.11415714090799

5-й корень [ 1.11; 1.12]

x = 1.11415714084615

6-й корень [ 2.77; 2.78]

x = 2.77260470827241

7-й корень [ 6.43; 6.44]

x = 6.43911723843485

8-й корень [ 9.31; 9.32]

x = 9.31724294144078

3) 2 x ² – 5 = 2 ^x

Контроль

1-й корень [-1.64;-1.63]

x = -1.63137672535049

2-й корень [ 2.18; 2.19]

x = 2.18478845171194

3-й корень [ 6.13; 6.14]

x = 6.13493835514964

4) 4 x ⁴ – 6,2 = cos0,6 x

Контроль

1-й корень [-1.15;-1.14]

x = -1.14899614950809

2-й корень [ 1.14; 1.15]

x = 1.14899614952083

5) ln(x + 6,10 = 2sin(x – 1,4)

Контроль

1-й корень [-5.93;-5.92]

x = -5.92148540437483

2-й корень [-4.73;-4.72]

x = -4.72227504245529

3-й корень [-2.45;-2.44]

x = -2.44636594824988

6) 2^{- x} = 1 – 0,5 x ²

Контроль

1-й корень [-2.69;-2.68]

x = -2.68003383521864

2-й корень [ 4.46; 4.47]

x = 4.46197840075183

7) 5sin2x = sgrt(1-x)

Контроль

1-й корень [-18.32;-18.31]

x = -18.31275351383374

2-й корень [-17.81;-17.80]

x = -17.80359794106334

3-й корень [-15.24;-15.23]

x = -15.23931500948675

4-й корень [-14.60;-14.59]

x = -14.59236215599230

5-й корень [-12.17;-12.16]

x = -12.16045625391416

6-й корень [-11.39;-11.38]

x = -11.38599320170761

7-й корень [-9.09;-9.08]

x = -9.08077073001186

8-й корень [-8.18;-8.17]

x = -8.17946302043856

9-й корень [-6.01;-6.00]

x = -6.00429034909757

10-й корень [-4.97;-4.96]

x = -4.96761637068994

11-й корень [-2.94;-2.93]

x = -2.93754330773299

12-й корень [-1.74;-1.73]

x = -1.73949286292191

13-й корень [ 0.09; 0.10]

x = 0.09567866423583

Построить таблицу истинности для данной логической схемы:

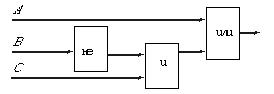
Таблица истинности построена так.

По заданной схеме записано соответствующее ей логическое выражение.

Получаем 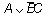(знак конъюнкции пропущен).

Строим соответствующую ему таблицу истинности.

Примечание. В действительности логические элементы обозначаются не так, как в приведенном примере; их обозначения приведены в билете № 9. В заданиях ниже используются именно такие обозначения.

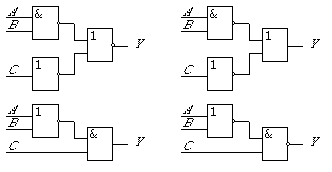
Задания

Построить таблицу истинности для данных логических схем.

Литература

1. Введение в информатику. Лабораторные работы. / Авт.-сост. А.П. Шестаков; Пермский университет. Пермь, 1999, ч. I, 56 с.

Дата добавления: 2015-04-23