Дендрограмма. Основные характеристики кластеров

Методы объединения объектов.

y – эмпирическое значение

y* - теоретическое значение

p – число параметров уравнения

Графическое изображение процесса объединения кластеров. Бывает вертикальная и горизонтальная.

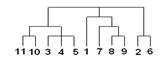
Основные характеристики кластеров.

Центр кластера - среднее геометрическое место точек в пространстве переменных. Радиус кластера - максимальное расстояние точек от центра кластера. Спорный объект - объект, который может быть отнесен к нескольким кластерам. Размер кластера может быть определен либо по радиусу кластера, либо по среднеквадратичному отклонению объектов для этого кластера.Объект относится к кластеру, если расстояние от объекта до центра кластера не больше радиуса кластера. Если это условие выполняется для двух и более кластеров, объект является спорным.

11. Факторный анализ – совокупность методов, которые на основе объективно существующих корреляционных взаимосвязей признаков (или объектов) позволяют выявлять скрытые обобщающие характеристики структуры изучаемых объектов и их свойств.

Цели: сокращение числа переменных и определение структуры взаимосвязи между ними.

Под фактором понимается гипотетическая, латентная переменная, которая имеет линейные корреляционные связи с исходными измеряемыми переменными.

Этапы:

1. Построение матрицы попарных корреляций.

2. Выделение факторов – Метод Главных Компонент.

(осуществляет переход к новой системе координат F1,..., Fp в исходном пространстве признаков X1,..., Xk).

Идея МГК:

Линейные комбинации выбираются таким образом, что среди всех возможных линейных нормированных комбинаций исходных признаков первая ГК F1 (х) обладает наибольшей дисперсией.

Геометрически - это ориентация новой координатной оси F1 вдоль направления наибольшей вытянутости эллипсоида рассеивания объектов исследуемой выборки в пространстве признаков X1,…, Xk.

Вторая ГК имеет наибольшую дисперсию среди всех оставшихся линейных преобразований, некоррелированных с первой главной компонентой.

3. Вращение матрицы факторных нагрузок.

Методы вращения матрицы факторных нагрузок: варимакс (для столбцов – минимизируется число переменных), квартимакс (для строк – минимизируется число факторов), эквамакс (комбинация варимакс и квартимакс).

4. Определение признаков, объединившихся в каждом факторе.

Что дает факторный анализ? Объединяет связанные исходные признаки в подгруппы и позволяет более наглядно представить взаимное расположение имеющихся подгрупп наблюдений.

12. Дисперсионный анализ – параметрический метод для проверки значимости различий, применяемый, когда нас интересуют сравнение двух и более выборок.

Внутригрупповая вариация измеряет, насколько неоднородна каждая выборка.

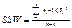
n_i – количество объектов в i-й выборке,
S_i – стандартное отклонение i-й выборки,
n – общее количество исследуемых объектов,
k – количество степеней свободы (выборок).

Межгрупповая вариация отражает, насколько различаются выборочные средние.

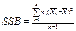
Вывод по ДА:

Если F_эмп < F_кр → H0 (Наблюдаемые расхождения в значениях выборочных средних можно объяснить случайностью!)

Если F_эмп ≥ F_кр → H1 (Наблюдаемые расхождения в значениях выборочных средних нельзя объяснить лишь случайностью!)

Виды ДА:

сколько факторов принимает участие в исследовании (однофакторный, многофакторный),

сколько переменных подвержены действию факторов (одномерный, многомерный),

как соотносятся друг с другом выборки значений (связанных, несвязанных выборок).

13

14.1. значения статистических показателей, которые представлены в определенной хронологической последовательности. Элементы ряда: по оси у- показатели, кот харак-ют исследуемый объект, по х-показатели периодов времени (месяц, год, декада).

Виды динамических рядов

- моментный ряд отражает значения показателей на определенный момент времени

- интервальный ряд содержит значения показателей за определенные периоды времени. В интервальном ряду уровни можно суммировать, получая накопленные итоги.

Цели анализа динамических рядов (анализа изменений во времени):

-Прогнозирование тенденций, предсказание значений;

-Оценка эффективности существующих методов управления, оценка текущего состояния;

-Исследование социально-экономических явлений.

14.2.

Аналитическое выравнивание ряда динамики

Основным содержанием метода аналитического выравнивания рядов динамики является расчет общей тенденции развития как функции времени: где

уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает основную тенденцию развития ряда динамики.

Простейшими моделями (формулами), выражающими тенденцию развития, являются следующие:

линейная функция - прямая

показательная функция

степенная функция - кривая второго порядка (парабола)

Расчет параметров функции обычно производится методом наименьших квадратов (МНК), в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическим и эмпирическим уровнями:

Параметры уравнения, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выровненные уровни.

14.3 Способы «механического» сглаживания колебаний путем усреднения значений ряда относительно других, расположенных рядом, уровней ряда.

а) Метод усреднения по двум половинам ряда: ряд делится на две части. Рассчитываются два значения средних уровней ряда, по которым графически определяется тенденция ряда.

б) Метод укрупнения интервалов: производится увеличение протяженности временных промежутков, и рассчитываются новые значения уровней ряда.

в) Метод скользящего среднего: основан на расчете средних уровней ряда за определенный период, для характеристики тенденции развития исследуемой статистической совокупности.

и т.д.

Скользящее среднее при усреднении за год – тренд * цикличность * сезонность.

Тренд - устойчивое систематическое изменение процесса в течение продолжительного времени.

14.4. Способы «аналитического» выравнивания, т. е. определения сначала функционального выражения тенденции ряда, а затем новых, расчетных значений ряда.

-при равномерном развитии — линейная функция: Yt = b0 + b1t;

-при росте с ускорением: парабола второго порядка: Yt = b0 + b1t + b2t2; кубическая парабола: Yt = b0 + b1t + b2t2 + b3t3;

-при постоянных темпах роста — показательная функция: Yt = b0b1t;

-при снижении с замедлением — гиперболическая функция: Yt = b0 + b1/t.

14.5. Модель, которая статистически описывает связи значений одного и того же показателя в различные моменты времени Y (t) = f (y(t-1)). Авторегрессия часто используется в качестве линейной модели для прогнозирования. В общем виде она описывается выражением

,

где n - число независимых переменных с коэффициентом dj для каждой xj, k - число задержек (лагов) для зависимой переменной y. Тогда общее число параметров модели будет k+n. Задача заключается в оценке параметров b и d. Таким образом, чем длиннее задержка, тем больше параметров авторегрессионной модели требуется оценить.

14.6. 1). MAS – ср. абс. отклонение. . 2). MSE – среднеквадратич. ошибка . 3). MAPE – ср. ошибка аппроксимации (5-7%) – хорошее ур-ие тренда. Средне абсолютная процентная ошибка. 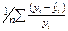. Эти критерии д. иметь мин. знач-ие, ориентирующее на лучшее ур-ие. В кач-ве критериев м. использ-ть: 1. макс. знач-ие критерия Фишера F→max. 2. макс. знач-ие коэф-та детерминации . Выбранное на основе критериев ур-ие тренда не всегда м. признать моделью тренда, пригодной для погнозирования. Необходимо, чтобы стат. значимы были параметры ур-ия тренда (оценивается по t – статистике) и стат. значимо было ур-ие в целом (F – критерий): 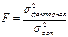. Важнейшим критерием оценки кач-ва трендовой модели явл-ся оценка автокорр-ции в остатках. . - остаток. Автокорр-ция – завис-ть остатков периода t от остатков предшеств. непосредственно данному периода или отделённого но опред. интервал, называемый лагом. Наличие автокорр-ции в остатках говорит о сохранении тенденции в остатках, т.е. построенная трендовая модель не полностью описывает основную тенденцию ряда.

14.7. Индекс сезонности – процентное отношение средней величины из фактических уровней одноименных месяцев к средней величине из выровненных уровней одноименных месяцев (минимум 3 года).

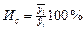
Индекс сезонности = Среднее значение (данные/скользящее среднее) за сезон

Значение с поправкой на сезон = данные / индекс сезонности.

Прогноз = Тренд * Индекс сезонности.

14.8. Базисные показатели характеризуют итоговый результат всех изменений в уровнях ряда от периода базисного уровня до данного (i-го) периода.

Цепные показатели характеризуют интенсивность изменения уровня от одного периода к другому в пределах промежутка времени исследования.

выражает абсолютную скорость изменения ряда динамики, определяется как разность между данным уровнем и уровнем, принятым за базу сравнения.

Абсолютный базисный прирост

где y_i - уровень сравниваемого периода; y₀ - уровень базисного периода.

Абсолютный цепной прирост (скорость роста)

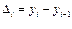
где y_i – уровень сравниваемого периода; y_i-1 – уровень предшествующего периода.

Коэффициент роста показывает относительную скорость изменения ряда, определяется как отношение данного уровня к предыдущему или базисному.

Коэффициент роста базисный:

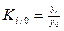
Коэффициент роста цепной:

Если коэффициент роста выражается в процентах, то его называют темпом роста.

Темп прироста базисный:

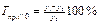
Темп прироста цепной:

15.1. комплекс мероприятий и нормативных документов, направленных на поддержание качества продукции (услуг) на заданном уровне.

КК определяется тем на сколько контролируется процесс. Процесс - любой вид деятельности, который превращает ресурсы в продукты

Как провести КК:

1.100% выходной контроль

2.Выборочный контроль (выбираем 1% товара от всей партии в разное время)

3.а)Диаграмма Парето Графическое представление степени важности факторов.

-По результатам деятельности - отражает нежелательные результаты в сферах:

а)производства, б)себестоимости, в)поставок…
-По причинам -отражает причины: а)по кадрам, б)по оборудованию, в)по сырью, г)по методам работы…

б)Гистограммы- устанавливают верхнюю и нижнюю границы допуска.

в)Построение контрольных карт

Для построения Кк:

-Замеры параметров процесса

-Центральная(осевая) линия

-Контрольные границы

Построение Х и R- карт:

Х-карта:

Стандарт задан:

Центральная линия μ

Контрольные границы µ±Aσ

Стандарт не задан:

Центральная линия х

Контрольные границы X±A2R

R- карта:

Стандарт задан:

Центральная линия dσ

Контрольные границы От D1σ до D2σ

Стандарт не задан:

Центральная линия R

Контрольные границы От D3R до D4R

P - карта

Средняя доля несоответствующих единиц:

Центральная линия

Контрольные границы

НКГ, ВКГ

Средний объем подгруппы

Анализ процесса

1.Выход процесса из управляемого состояния- Выход за контрольные границы.

Требуется немедленное вмешательство!

2."Опасные" ситуации:

-«Серия»7 и более точек подряд или 10 из 11 последовательных точек находятся по одну сторону от центральной линии.

- «Тренд»-Точки образуют повышающуюся или понижающуюся ломаную

- Приближение к контрольным границам 2 или более точек на расстоянии более 2 б от центральной линии

- Периодичность

Требуют анализа причин их возникновения.

15.2.

Кривая Парето (диаграмма Парето) — графическое отражение закона Парето, кумулятивной зависимости распределения определённых ресурсов (накопленного богатства, результаты голосования…) или результатов от большой совокупности (выборки) причин (например, от количества населения, активности участников…).

15.3.

Гистогра́мма (от др.-греч. ἱστός — столб + γράμμα — черта, буква, написание) — способ графического представления табличных данных.

Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра.

Таким образом, гистограмма представляет собой графическое изображение зависимости частоты попадания элементов выборки от соответствующего интервала группировки.

15.4.

Контрольные карты — график изменения параметров выборки, обычно средних и среднеквадратичного отклонения. Различают контрольные карты для количественного и качественного признаков. Цель построения контрольной карты — выявление точек выхода процесса из устойчивого состояния для последующего установления причин отклонения и его устранения.

Для контроля по непрерывному признаку обычно строятся X-, R или S карты. На X- карту наносятся значения выборочных средних для того, чтобы контролировать отклонение от среднего значения непрерывной переменной (например, размера поршневого кольца, прочности материала и других подобных параметров). На контрольную карту типа R наносятся значения размахов выборок для контроля за степенью изменчивости непрерывной величины, а на S и S**2 картах строятся соответственно графики выборочных стандартных отклонений и дисперсий.

Для контроля качества продукции по альтернативному признаку используются C, P, U и Np карты. На С картах строится график числа дефектов (в партии, в день, на один станок, в расчете на 100 метров трубы и т.п.), а контрольные пределы для данного типа карт рассчитываются на основе распределения Пуассона. На U карте строится график относительной частоты дефектов (отнесенных, например, к числу метров трубы или объему партии деталей). На контрольных картах типа Np так же, отображается число дефектов, однако контрольные пределы этой карты рассчитываются на основе биномиального распределения. На картах типа P строится график процента обнаруженных дефектных изделий с вычислением контрольных пределов на основе биномиального распределения.

Стадии статистического анализа при использовании карт контроля

1. Выбор параметров процесса для измерения и составления КК.

2. Изучение КК для определение трендов и исключительных случаев.

3. Вычисление обобщающих параметров процесса.

4. Принятие решения о том, находится ли процесс под контролем.

15.5.

15.6.

16.1. К индексам относят величины, количественно характеризующие сводную динамику, те изменение во времени и в пространстве уровня изучаемого общественного явления

Индексы делятся на Индивидуальные - индексы, которые характеризуют изменение только одного элемента совокупности. Сводные - характеризует изменение по всей совокупности элементов сложного явления.

1.определяют средние изменения сложных, непосредственно несоизмеримых совокупностей во времени;

2.устанавливают средние отношения сложных явлений в пространстве;

3.оценивают среднюю степень выполнения плана по совокупности в целом или ее части;

4.определяют роль отдельных факторов в общем изменении сложных явлений во времени или в пространстве и, в частности, изучается влияние структурных сдвигов.

Средние взвешенные индексы

· Средний взвешенный арифметический индекс цен

· Средний взвешенный гармонический индекс цен

Агрегатный территориальный индекс цен

где pA pB - цена за единицу продукции каждого вида соответственно на территории А и В;

qA - количество выработанной или реализованной продукции каждого вида по территории А (в натуральном выражении).

Дата добавления: 2015-04-24