Индексный метод изучения динамики среднего уровня

Индексы динамики среднего уровня - эти индексы особого рода характеризуют динамику средней величины во времени. Они вычисляются всегда для однородной продукции.

Этот индекс показывает, во сколько раз изменилась цена реализации товара А в отчетном периоде по сравнению с базисным.

В ряде случаев приходится изучать динамику общественных явлений, уровни которых выражены средними величинами (средней себестоимостью, средней заработной платой, средней урожайностью, продуктивностью животных, средней производительностью труда и т.д.).

Динамика средних показателей зависит от одновременного изменения вариантов, из которых формируются средние, и изменения удельных весов этих вариантов, т.е. от структуры изучаемого явления. Так, например, средняя производительность труда на предприятии может возрасти за счет ее повышения у рабочих отдельных специальностей и повышения удельного веса рабочих с более высокой производительностью труда в общей численности рабочих. Динамика средних надоев молока по региону зависит от динамики средних надоев в каждом хозяйстве, повышения удельного веса хозяйств с более высокими надоями в общем числе хозяйств.

Таким образом, на изменение динамики среднего значения изучаемого явления могут оказывать влияние одновременно два фактора: изменение осредняемого показателя и изменение структуры. Изучение совместного действия указанных факторов на общее изменение динамики среднего уровня явления, а также роли и влияния каждого фактора в отдельности в общей динамике средней проводится в статистике при помощи системы взаимосвязанных индексов.

Так как величина индекса зависит от весов, то и здесь возникает вопрос о весах средних. В связи с этим различают индексы переменного и фиксированного состава. Рассмотрим их построение и содержание на примере индекса себестоимости продукции. Очевидно, что на его величину влияют не только изменения себестоимости единицы продукции в каждой фирме, но и изменения роли отдельных фирм в общем объеме выпускаемой продукции. Общий индекс, в котором отражается влияние этих двух факторов, определяем как отношение следующих двух средних:

с1(ср)= сумма(с1q1) / сумма(q1) и c0(ср)=сумма(с0q0) / сумма(q0) и

I(c(ср))=с1(ср) / c0 = (сумма(c1q1)/сумма(q1)) / (сумма(c0q0)/сумма(q0))

Индексы, отражающие изменение средних величин за счет влияния только индексируемых величин при постоянных весах, называются индексами фиксированного (постоянного) состава.

Отношение двух взвешенных средних с меняющимися (переменными) весами, показывающее изменение индексируемой величины, называется индексом переменного состава.

Разложение общих индексов на факторные также дает возможность определить роль отдельных факторов в общем изменении явления не только в относительном, но и в абсолютном выражении.

Изучение динамики средних показателей индексным методом возможно только после разбивки данных совокупности на группы по признакам, характеризующим структурные сдвиги, и вычисления групповых средних. Таким образом, применение индексного метода для проведения факторного анализа и изучения структурных сдвигов тесно связано с методом группировок.

Систему взаимосвязанных индексов для анализа динамики средних показателей можно представить в следующем виде:

I(x(ср)) = x1(ср)/x0(ср)= (сумма(x1f1)/ сумма(f1)) / (сумма(x0f0)/ сумма(f0)) (*Iперемен. состава*) = [(сумма(x1f1)/ сумма(f1)) / (сумма(x0f1)/ сумма(f1))]*[(сумма(x0f1)/ сумма(f1)) / (сумма(x0f0)/ сумма(f0))]

где х₁ и x₀ - уровни осредняемого показателя соответственно в отчетном и базисном периодах;

f₁ и f₀ - веса (частоты) осредняемых показателей соответственно в отчетном и базисном периодах.

В указанной системе взаимосвязанных индексов при построении индекса фиксированного состава в качестве весов принята структура отчетного периода, что позволяет нам проследить изменение средней динамики изучаемого явления только за счет изменения осредняемых значений качественного показателя. При построении индекса структурных сдвигов в качестве соизмерителя принята величина осредняемого показателя на уровне базисного периода, что дает возможность изучить изменение средней динамики явления только за счет структурных сдвигов.

Дисперсия, коэффициент вариации, определение вариации для сгруппированных данных.

Наряду со средней величиной, характеризующей типичный уровень варьирующего признака, около которого колеблются отдельные значения признака, рассматривают показатели вариации (колеблемости) признака, позволяющие количественно измерить величину этой колеблемости.

К показателям вариации относят: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Простейшим показателем вариации является размах вариации, который рассчитывается по следующей формуле:

R = Xmax – Xmin,

где Xmax, Xmin - соответственно, максимальное и минимальное значения признака в исследуемой совокупности.

Размах вариации характеризует диапазон колебаний признака в изучаемой совокупности и измеряется в тех же единицах, в которых выражен признак.

Рассчитывают среднее линейное отклонение, которое бывает невзвешенное и взвешенное. Если каждое значение признака встречается в совокупности один раз, то применяется формула среднего линейного отклонения невзвешенного:

,

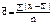где x - значение признака;

n - количество вариант.

Среднее линейное отклонение характеризует абсолютный размер колеблемости признака около средней и измеряется в тех же единицах, в которых выражен признак.

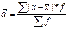
Наиболее точным показателем вариации является среднее квадратическое отклонение. Для его определения предварительно рассчитывают показатель дисперсии. Дисперсия невзвешенная определяется по формуле:

σ² = .

Тогда, соответственно, для расчета среднего квадратического отклонения используют формулу:

σ = .

Как и среднее линейное отклонение, среднее квадратическое отклонение характеризует абсолютный размер колеблемости признака около средней, однако является более точной характеристикой.

В отличие от среднего линейного и среднего квадратического отклонения коэффициент вариации является мерой относительной колеблемости признака около средней и характеризует степень однородности признака в изучаемой совокупности. Он определяется по формуле:

V = ´ 100%.

Дата добавления: 2015-04-24