Побудова фазового портрету системи. Поле напрямків. Метод ізоклин

Сепаратриси

Сепаратриса – траєкторія динамічної системи з двома фазовими просторами, які прямують до сідлового стану рівноваги при t→∞ (стійка сепаратриса) чи при t→–∞ (нестійка сепаратриса). Якщо сепаратриса прямує до сідла при t→±∞, то її разом з сідлом називають петлею сепаратриси. В диcипативних ДС з петлі сепаратриси може розвинутись граничний цикл.

В консервативних ДС петлі ділять фазовий простір на області з різною поведінкою траєкторій.

Для ДС з розмірністю фазового простору >2, стійкі і нестійкі різномініття сідлових станів рівноваги і/або сідлових граничних циклівназиваються багатовимірними сепаратрисами (вони можуть ділити фазовий простір на області притягування різних атракторів).

Пов'язані з сепаратристськими різноманіттями біфуркації можуть призводити до виникненнядивних атракторів, напр. атрактор Лоренца зароджуєтсья в момент, коли нестійкі сепаратриси сідла перетинаються стійкими різноманіттями сідлових граничних циклів.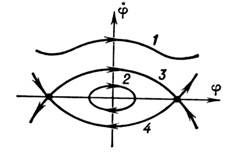

1 – траєкторія, що відповідає коливальному руху, 2 – обертовому руху, 3 і 4 – сепаратриси.

Розв'язки, що відповідають сепаратрисам описують клас відокремлених хвильв нелінійних середовищах з дисперсією, а також різного роду дислокації, дисклінації...

Найцікавіші результати з якісного моделювання властивостей біологічних систем отримані на моделях з двох диференціальних рівнянь, які допускають якісне дослідження за допомогою методу фазової площини.Розглянемо систему двох автономних звичайних диференціальних рівнянь загального вигляду

P (x, y), Q (x, y) – неперервні функції, визначені в деякій області G евклідової площини (x, y – декартові координати) і мають неперервні похідні порядку не нижче першого.

Область G може бути як необмеженою, так і обмеженою. Якщо змінні x, y мають конкретний біологічний сенс (концентрації речовин, чисельності видів) найчастіше область G являє собою позитивний квадрант правої півплощини:

0£ x< ¥, 0 £ y < ¥.

Концентрації речовин або чисельності видів також можуть бути обмежені зверху об'ємом посудини або площею ареалу проживання. Тоді область значень змінних має вигляд:

0 £ x < x₀, 0 £ y< y_{0 .}

Змінні x, y в часі змінюються відповідно до системи рівнянь, так що кожному стану системи відповідає пара значень змінних (x, y).

 

Кожній парі змінних(x, y) відповідає певний стан системи.
Розглянемо площину з осями координат, на яких відкладені значення змінних x, y. Кожна точка М цій площині відповідає певному стану системи. Така площина зветься фазовою площиною і забражує сукупність усіх станів системи. Точка М (x, y) називається зображувальною або представляючою точкою.

Нехай в початковий момент часу t = t₀ координати зображувальної точки М₀ (x(t₀), y(t₀)). У кожен наступний момент часу t зображувальна точка зміщуватиметься відповідно до змін значень змінних x(t), y(t). Сукупність точок М (x(t), y(t)) на фазовій площині, положення яких відповідає станам системи в процесі зміни в часі змінних x(t), y(t) відповідно до рівнянь, називається фазовою траєкторією.

Сукупність фазових траєкторій при різних початкових значеннях змінних дає легко доступний для огляду "портрет" системи. Побудова фазового портрета дозволяє зробити висновки про характер змін змінних x, y без знання аналітичних рішень вихідної системи рівнянь. Для зображення фазового портрету необхідно побудувати векторне поле напрямків системи в кожній точці фазової площини. Ставлячи приріст D t>0, отримаємо відповідні прирости D x і D y з виразів:

Dx=P(x,y) Dt,

Dy=Q(x,y) Dt.

Напрям вектора dy/dxв точці (x, y) залежить від знаку функції P(x, y), Q(x, y) і може бути заданий таблицею

P(x,y)>0, Q(x,y)>0
P(x,y)<0, Q(x,y)<0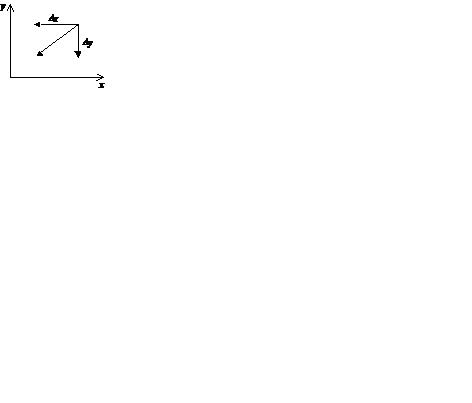
P(x,y)>0, Q(x,y)<0
P(x,y)<0, Q(x,y)>0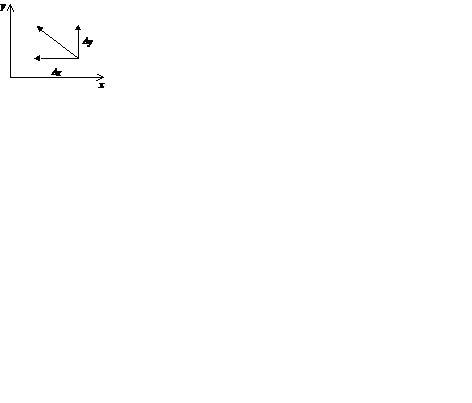

або інакше

Розв'язок цього рівняння y = y(x, c), або в неявному вигляді F(x, y) = c, де с – стала інтегрування, дає сім'ю інтегральних кривих рівняння фазових траєкторій системи на площині x, y.

Постановка завдання. Для диференціального рівняння F(x, y, y') = 0 (1) або y' = f(x, y) (2) методом ізоклин побудувати інтегральну криву, що проходить через точку M₀(x₀, y₀).

План розв'язку. Теорема (Коші). Якщо функція f(x, y) неперервна в точці M₀(x₀, y₀) і в її околі, то існує розв'язок y = y(x) рівняння такий, що y(x₀) = y₀. Якщо неперервна також частинна похідна ∂f/∂y даної функції, то це рішення єдине.

Задача Коші для диференціального рівняння першого порядку має наступне формулювання: Знайти розв'язок y = y(x) (інтеграл ψ(x, y) = 0) диференціального рівняння, який задовольняє початковій умові y(x₀) = y₀ (ψ(x₀,y₀)=0). З геометричної точки зору це означає, що серед інтегральних ліній даного рівняння необхідно знайти ту, яка проходить через задану точкуM₀(x₀, y₀).

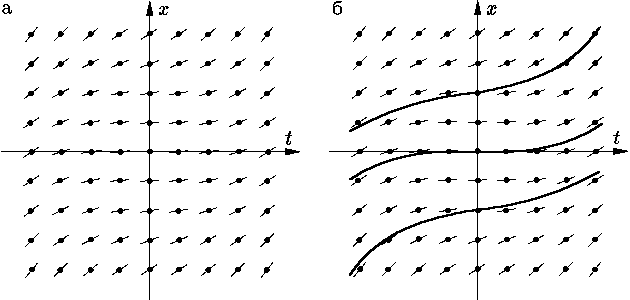
Геометрична інтерпретація диференціального рівняння (2) полягає в тому, що воно в кожній точціM(x, y), що належить областіD, в якій виконуються всі умови теореми Коші, задає напрямy' = tgα = kдотичний до єдиної інтегральної лінії рівняння (2), що проходить через точкуM(x, y), тобто поле напрямків в областіD.

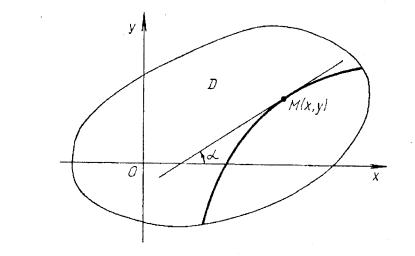
В областіD для рівняння (2) можна виділити однопараметричну сім'юліній f(x, y) = k = const, кожна з яких називається ізоклиною. Як випливає з визначення, уздовж кожної ізоклини поле напрямків постійне, тобто y' = k = const.

Знаходження ізоклин і напрямів вздовж них дозволяє впорядкувати поле напрямків і наближено побудувати інтегральні лінії даного диференціального рівняння, тобто графічно проінтегрувати це рівняння.

Дата добавления: 2015-05-08