Зразки розв’язання задач 2 страница

	БЗ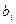

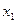
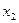
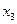
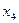
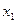
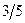
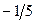
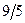
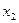
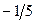
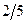
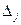
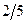
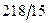
Знайдемо дробові частини чисел

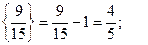
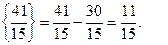
Порівняємо

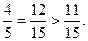
Враховуючи дробові частини чисел 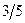і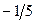

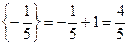складемо додаткові обмеження цілочислові для першого рядка 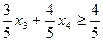або 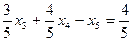і введемо додатковий рядок таблиці

	БЗ
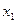
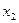
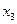
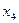
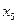
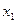
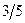
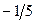
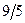
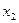
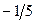
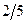
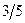
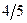
						-1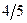

	БЗ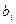
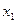
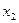
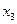
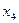
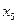
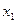
					-1

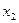
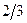
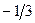
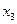
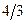
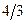
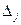
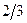
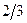
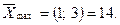
Графічний метод

Областю припустимих розв’язків є чотирьохкутник ОАВС, а .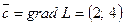

Оптимальний розв’язок задача має у точці В

.

Одержане оптимальне значення не є цілочисловим. Замінимо багатокутник ОАВС на ОКЕМNF. Лінія рівня переміщується у точку 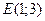де і є максимальне значення цільової функції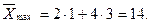

Таким чином, підприємству необхідно придбати 1 комплект обладнання першого виду і 3 комплекти обладнання другого виду, що забезпечить йому при наявних обмеженнях на виробничі площі і грошові кошти максимальне збільшення випуску продукції, яке дорівнює 14 тис. грн. за зміну.

Задача 5

Дослідити функцію на екстремум

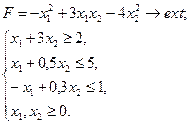
1. Побудуємо область обмежень

1.

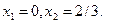
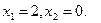
2.

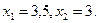
3.

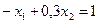
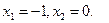
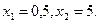
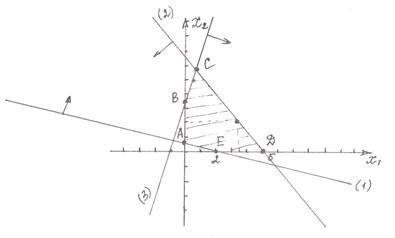
Областю обмежень є множина точок площини ХОУ, що належать чотирьохкутнику АВСDE з вершинами:

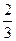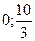А (0; ); В(); С(1,25; 7,5); D(5; 0); E(2; 0)

1. Знайдемо значення функції у критичних точках області

- критична точка, що не належить області розв’язків.

1. Знайдемо значення функції у критичних точках на границях області.

1) ;

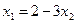
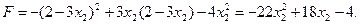
- критична точка, що належить області розв’язків.

2) ; .

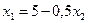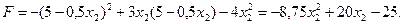
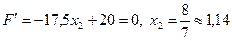
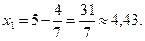Критична точка 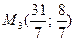належить області розв’язків, тому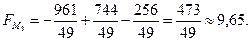

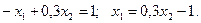
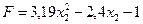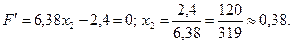
3) ; 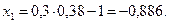Критична точка не належить області розв’язків.

4. Знайдемо значення функції у вершинах області розв’язків

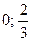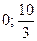А (); В(); С(1,25; 7,5); D(5; 0); E(2; 0)

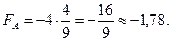
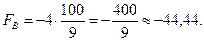
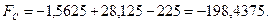
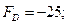
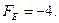
Значить: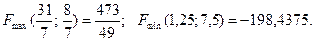

Задача 6

Гірничо-збагачувальний комбінат виробляє товарну продукцію – концентрат, який реалізує на внутрішній і зовнішній ринки збуту. При продажу 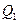тон концентрату на внутрішній ринок витрати на реалізацію складають грн., а при продажу тон концентрату на зовнішній ринок - 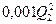грн.

Визначити, яку кількість концентрату (тон) необхідно продавати на внутрішній і зовнішній ринки, щоб витрати на реалізацію були мінімальними, якщо за рік реалізується 10000 тис. тон концентрату.

Розв’яжемо задачу за допомогою методу множників Лагранжа

Складемо економіко-математичну модель задачі. Цільова функція економіко-математичної моделі має вигляд

,

де 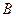- витрати на реалізацію концентрату, грн.

при обмеженнях

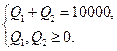
Складемо функцію Лагранжа

.

За необхідною умовою існування екстремуму функції, знайдемо частинні похідні функції за змінними 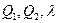, прирівняємо їх до нуля та одержимо систему рівнянь

Після елементарних перетворень одержуємо

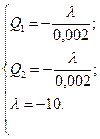
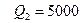Звідки тис. тон; тис. тон.

Перевіримо одержані значення на оптимальність. Використаємо достатню умову екстремуму функції двох змінних.

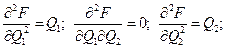
Одержуємо, Звідси, 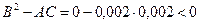, тому у точці (5000; 5000) існує екстремум функції. При 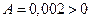одержуємо, що у досліджуваній точці існує мінімум функції, значить, мінімальні витрати на реалізацію концентрату дорівнюють

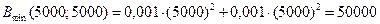грн.

Задача 7

Для виробництва двох видів продукції виробів А і В підприємство використовує три типи технологічного обладнання. Кожен із виробів повинен пройти обробку на кожному з типів обладнання. Час обробки кожного з виробів, витрати, що пов’язані з виробництвом одного виробу, задано у таблиці

Тип обладнання	Витрати часу на обробку одного виробу, час.
А	В
І
ІІ
ІІІ
Витрати на виробництво одного виробу, тис. грн.

Обладнання І і ІІІ типів підприємство може використовувати не більше 26 і 39 годин відповідно, обладнання ІІ типу доцільно використовувати не менше 4 год.

Визначити, скільки виробів кожного виду треба виробити підприємству, щоб середня собівартість одного виробу була мінімальною.

Позначимо 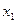- кількість виробів виду А; 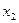- кількість виробів виду В. Загальні витрати на їх виробництво складають 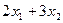тис. грн., а середня собівартість одного виробу дорівнює 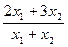, тому математична модель задачі має вигляд

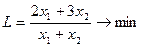
при обмеженнях

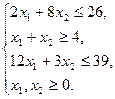
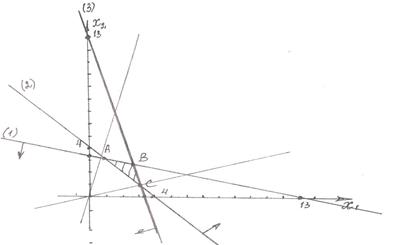
Побудуємо область припустимих розв’язків – трикутник АВС.

Із цільової функції виразимо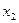

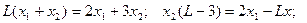
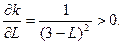
Значить кутовий коефіцієнт прямої 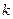зростає, тобто пряма обертається проти годинникової стрілки і у точці С є мінімум, а у точці А – максимум.

Знайдемо координати точки С

.

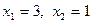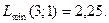
Тому підприємство повинно випускати 3 вироби виду А і 1 виріб виду В, при цьому середня собівартість буде складати 2,25 грн.

Задача №8

Наведена таблиця міжгалузевих зв’язків для 3 галузей промисловості. Необхідно визначити обсяги випуску продукції кожної галузі, якщо кінцевий продукт буде змінюватися і дорівнювати відповідно 40, 30 і 50 млн. грн.

Галузь промисловості	Обсяг продукції, млн. грн.	Міжгалузеві потоки в галузях, млн. грн.
№1	№2	№3

Для розв’язання застосуємо задачу про складання міжгалузевого балансу Леонтьєва

Складемо матрицю технології виробництва, використовуючи формулу

.

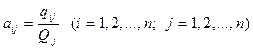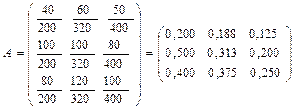
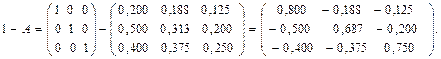
Знайдемо матрицю 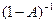, обернену до матриці (), визначник якої

.

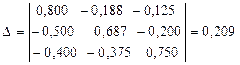Знайдемо алгебраїчні доповнення до елементів матриці ():

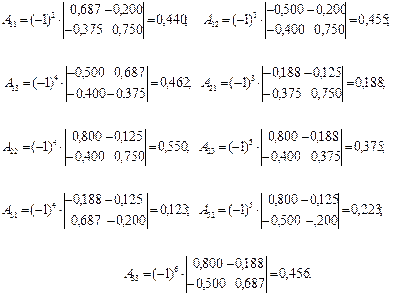
Тоді матриця коефіцієнтів сумісного споживання має вигляд

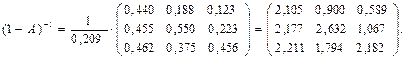
Обсяги продукції, які необхідно виробляти кожній галузі будуть дорівнювати

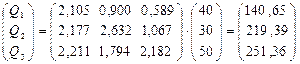
Таким чином, випуск продукції в першій галузі необхідно зменшити до 140,65 млн. грн., у другій – до 219,39 млн. грн., а у третій – до 251,36 млн. грн.

Задача 9

Міністерство розглядає пропозицію щодо нарощення виробничих потужностей для збільшення випуску однорідної продукції на чотирьох підприємствах, що належать даній галузі.

Для розширення виробництва міністерство виділяє кошти у обсязі 120 млн. грн. з дискретністю 20 млн. грн. Приріст випуску продукції на підприємствах залежить від суми виділених коштів, значення якого представлені у таблиці.

Кошти, млн. грн.	Приріст випуску продукції, млн. грн.
Підприємство №1	Підприємство №2	Підприємство №3	Підприємство №4

Знайти розподіл коштів між підприємствами, що забезпечує максимальний приріст випуску продукції, причому на одне підприємство може виділятися не більше однієї інвестиції.

Розв’яжемо задачу за допомогою методу динамічного програмування

Розіб’ємо розв’язок задачі на чотири етапи за кількістю підприємств, на які передбачається здійснити інвестиції.

Рекурентне співвідношення буде мати вигляд:

- для підприємства №1

- для всіх інших підприємств

.

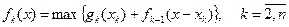Розв’язок будемо виконувати у відповідності до рекурентних співвідношень у чотири етапи.

1 етап.

Інвестиції надаємо тільки першому підприємству. Тоді:

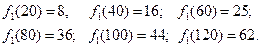
2 етап.

Інвестиції виділяємо першому і другому підприємствам. Рекурентне співвідношення для другого етапу має вигляд

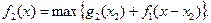
Тоді при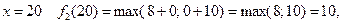

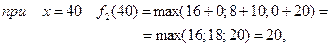
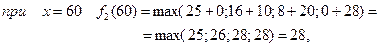
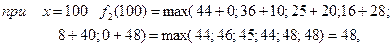
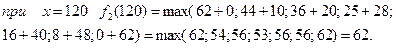
3 етап.

Фінансуємо другий етап і третє підприємство. Розрахунки виконуємо за формулою

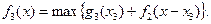
Тоді:

при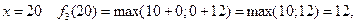

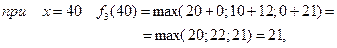
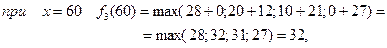
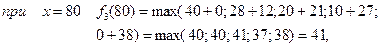
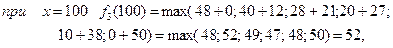
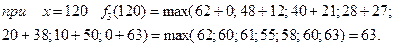
4 етап.

Інвестиції розміром 120 млн. грн. розподіляємо між третім етапом і четвертим підприємством

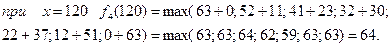
Одержано умови управління від першого до четвертого етапу. Повернемося від четвертого до першого етапу. Максимальний приріст випуску продукції у 64 млн. грн. одержано на четвертому етапі як 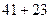, тобто 23 млн. грн. відповідають виділенню 40 млн. грн. четвертому підприємству (див. табл.). Відповідно до третього етапу 41 млн. грн. одержано як , тобто 21 млн. грн. відповідає виділенню 40 млн. грн. третьому підприємству. Відповідно до другого етапу, 20 млн. грн. одержано при виділенні 40 млн. грн. другому підприємству.

Таким чином, інвестиції обсягом 120 млн. грн. доцільно виділяти другому, третьому і четвертому підприємствам по 40 млн. грн., при цьому максимальний приріст продукції складе 64 млн. грн.

Дата добавления: 2015-05-23