Деформація в точці визначається як границя

Тензор деформацій.

1. Розглянемо спочатку лінійну деформацію, деформацію в одному вимірі.

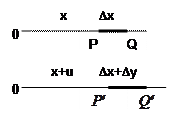Рис. 9. Деформація лінійного об'єкта.

У результаті деформації, наприклад, розтягання, точка Р переходить у положення 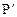, а точка Q – в. . Нехай PQ=D x. Тоді Р'^' =D x +D u. Деформація ділянки PQ (відносна зміна довжини):

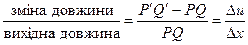
2. Деформація в площині.

Розглянемо в деякій площині точку Р с координатами x ₁ і x ₂.Нехай після деформації ця точка перемістилася так, що її координатами стали (x ₁+ u ₁) і (x ₂+ u ₂).

Вектор описує, таким чином, зсув довільно обраної точки деформуємого тіла. Він називається вектором деформації.

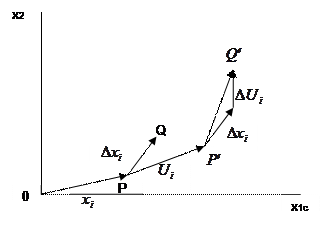Рис10. Деформація на площині.

Ми бачили, що у випадку лінійної деформації, деформація в точці (відносна деформація) виражається як частинна похідна від вектора деформацій по координаті (у випадку лінійної деформації вектор деформації має, природно, одну складову U). Тому в більш загальному випадку деформації в площині ми повинні утворити всі можливі часткові похідні від складових вектора деформації по координатах і проаналізувати їхній фізичний зміст.

У скороченому записі ці співвідношення мають вид:

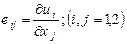
Величини представляють безрозмірні числа, малі в порівнянні з одиницею, оскільки теорія пружності розглядає лише малі деформації. Щоб з'ясуватиїхній геометричний зміст, звернемося до рис. 10.

Рис. 11. Геометрична інтерпретація компонентів двовимірного

тензора деформацій.

Розглянемо точку Q, яка лежить поблизу точки P.

.

Після деформації Q зміститься в положення Q`. - це сума двох векторів . - це різниця в зсувах двох точок P і Q спочатку розділених вектором . Далі, оскільки компоненти є функціями координат x₁ і x₂, ми можемо записати:

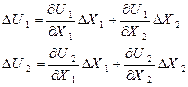(35)

Або, скорочено:

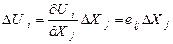(36)

Оскільки 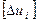і 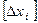є компонентами векторів, то [e_ij] є компонентами тензора 2-го рангу.

Тепер розглянемо два часткових випадки. Нехай вектор 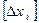у першому випадку буде рівнобіжний осі OX₁ (PQ₁), а в другому випадку - рівнобіжний осі OX₂ (PQ₂). Відповідне креслення дане на рис.11. При такому розгляді ми можемо встановити, як спотворюється прямокутний елемент у точці P.

Для PQ₁ ми повинна взяти 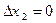і рівняння (35) приймають вид:

Зміст величин 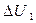і зрозумілий з рис. 11. Видно, що e₁₁ є зміною довжиною відрізка PQ₁ у напрямку OX₁, розраховане на одиницю довжини, оскільки

;

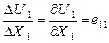e₂₁ вимірює поворот відрізка PQ₁ проти годинникової стрілки; кут на який відбувається поворот, задається його тангенсом:

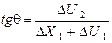
Оскількими розглядаємо лише малі по величині зсуву точок деформуємого тіла, U₁ і U₂ малі в порівнянні з x ₁, і,отже ∆U₁ і ∆U₂ малі в порівнянні з ∆ X₁. Таким чином,

У такий же спосіб, e₂₂ являє собою зміна довжини відрізка PQ₂ у напрямку осі OX₂, розраховане на одиницю довжини e₁₂, а вимірює мале обертання елемента довжини PQ₂ по годинниковій стрілці, по напрямку до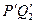

Тепер задамо собі питання: чи є тензор [e_ij] досить задовільною мірою деформації в точці P? Очевидно, у випадку позитивної відповіді під час відсутності деформації матеріалу в точці Р усі компоненти тензора повинні обертатися в нуль. Насправді це не відбувається. Дійсно, розглянемо обертання плоского елемента в його площині на малий кут ψ без деформації.

Обертання PQ₁ і PQ₂ здійснюються на кут ψпроти годинникової стрілки і, отже, з геометричного змісту величин e_ij, встановленого вище, випливає, що матриця тензора [e_ij] має вид:

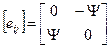(37)

Як бачимо, у цьому випадку деформація розглянутого елемента, відсутня, однак, не всі елементи тензора [e_ij] дорівнюють нулю.

Ми, таким чином, повинні виділити з тензора [e_ij] ту частину, що пов'язана з деформацією, але не пов'язана з просторовим переміщенням розглянутого об’єму без деформації, наприклад, з обертанням.

Любий тензор 2-го рангу може бути представлений у вигляді суми симетричного й антисиметричного тензора:

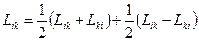
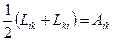
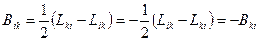
Представимо в такому виді тензор e_ij:

e_ij =u_ij+w_ij

де 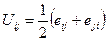і .

Вище ми бачили (формула (З7)), що тензор, що представляє собою чисте обертання, є антисиметричним. Симетрична частина тензора e_ijназивається тензором деформацій. Позначимо тензор деформацій через U_ik. Для розглянутого випадку плоскої задачі (деформація в площині) матриця тензора деформацій має вид:

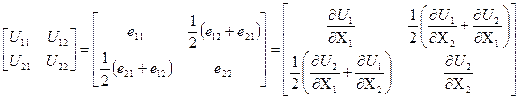
Рис. 12. Зсув при обертанні малого елемента у його площині,

що не деформується.

Тензор e_ij на відміну від тензора деформацій U_ik називається тензором відносних зсувів, як ми бачили, описує не тільки деформацію визначеного елемента пружного тіла, але і його поворот у просторі.

Поділ тензора e_ij на дві частини ілюструється рис.13.

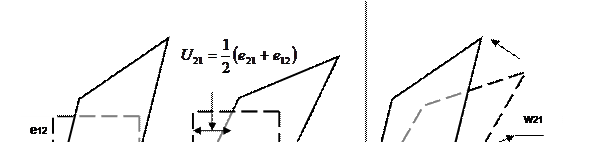
Рис. 13. Креслення, що ілюструє для двовимірного випадку те положення, що зсув точок деформуємого тіла в просторі складаються з деформацій матеріалу (центральна частина малюнка) і обертання елемента тіла як єдиного цілого, без деформації.

Діагональні елементи U₁₁ і U₂₂ тензора деформацій являють собою відносну зміну довжини відрізків плоского елемента рівнобіжних осям OX₁ і OX₂. Недіагональні елементи являють собою деформації зсуву; якщо два елементи довжини в недеформованому тілі рівнобіжні осям OX₁ і OX₂, те після деформацій кут між ними складає (центральна частина рис.13). Варто підкреслити, що недіагональний елемент тензора деформацій U₁₂ являє собою половину зміни кута між двома елементами довжини.

Дата добавления: 2015-05-24