І друга важливі границі та Їм супутні

Спираючись на властивості нескінченно малих функцій, встановимо деякі важливі властивості границь. Спочатку доведемо наступну теорему.

Теорема (про розкладання функції, яка має границю, на сталу і нескінченно малу).

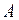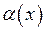Для того, щоб число було границею функції при , необхідно і достатньо, щоб виконувалась рівність , де – нескінченно мала при .

Доведення. Нехай спочатку . Тоді 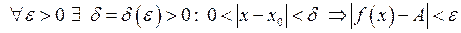. Це означає, що функція є нескінченно малою при . А тоді , де 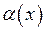– нескінченно мала при .

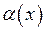Навпаки, нехай тепер , де – нескінченно мала при . Тоді 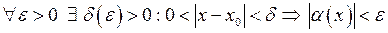. Тобто , а це й означає, що . Теорему доведено.

На підставі цієї теореми доведемо наступне твердження.

Теорема. Нехай . Тоді

а) ,

б) ,

в) якщо , то .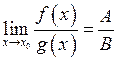

Доведення. На підставі попередньої теореми маємо:

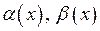, де – нескінченно малі при . Звідси:

, що на підставі тієї ж теореми дає: .

Далі: .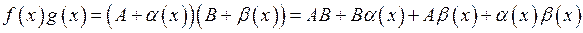

Величини – нескінченно малі при 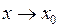, отже .

Для частки функцій маємо:

.

Покажемо, що другий доданок цього виразу є нескінченно мала при 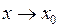. Дійсно, оскільки 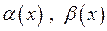– нескінченно малі при 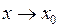, то , а також .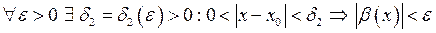

Покладемо , і оберемо . Тоді при виконанні нерівності 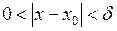буде виконано:

.

Звідси:

.

А оскільки – будь яке як завгодно мале додатне число, то за його рахунок і число також можна зробити як завгодно малим, тобто меншим, ніж будь яке, наперед задане число. Це й дає потрібне. Отже

.

Теорему доведено.

Відмітимо, що якщо – стала функція, то її границя , тобто дорівнює тій самій сталій. З цього факту і з теореми про границю добутку випливає властивість:

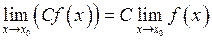, тобто сталий множник можна виносити за знак границі.

Приклад. Обчислити

.

Маємо:

.

Теорема (про граничний перехід у нерівностях).

Якщо у деякому околі точки (крім, можливо самої точки ) виконана нерівність , і існує , то виконана нерівність .

Доведення. Припустимо для визначеності, що виконана нерівність , і ця нерівність виконана в -околі точки (крім, можливо, самої цієї точки). Тобто, якщо , то . Припустимо, попри твердженню теореми, що 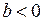. Тоді .

Або, що те ж саме: 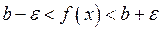. Оберемо так, щоб було (наприклад, ). Тоді у 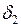-околі точки виконано 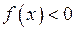. Позначимо . Тоді, якщо 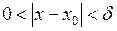, то водночас виконуються нерівності 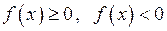, що неможливо. Отримане протиріччя і доводить теорему.

Зрозуміло, що, якщо в умові теореми нерівність замінити на 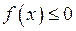, то тоді .

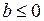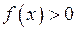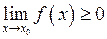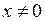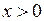Зауваження. Якщо в умові теореми нерівність замінити на , то твердження теореми зберігається, тобто , а не . Наприклад (при ), але . Або при , але .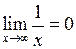

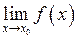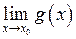Наслідок. Якщо в деякому околі точки (за винятком, може бути, самої цієї точки) виконана нерівність , і існують границі та , то

.

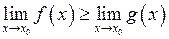Теорема. Якщо функція має скінчену границю при 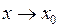, то ця функція обмежена у деякому околі точки .

Доведення. Оскільки існує , то

.

Звідси випливає, що -околі точки виконується нерівність:

.

Тепер, якщо функція невизначена у точці , то покладемо . А якщо ця функція визначені у точці , то покладемо . У будь якому випадку буде виконано в усьому -околі точки , що й означає обмеженість функції у цьому околі.

Зауваження. Зворотне твердження до цієї теореми, взагалі кажучи, несправедливе. Тобто з обмеженості функції у деякому околі точки не випливає існування границі функції у цій точці. Наприклад, функція 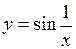обмежена у будь якому околі точки , а границі цієї функції при 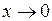не існує (див. лекцію 6). Для справедливості зворотного твердження необхідно накласти додаткові умови на функцію.

Теорема (про границю монотонної функції).

Якщо функція монотонна і обмежена у деякому околі точки (за винятком, може бути, самої точки ), то існує границя .

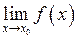Доведення цієї теореми виходить за межі нашого курсу*.

Теорема (про проміжну функцію).

Нехай в деякому -околі точки , за винятком, можливо, самої точки , визначені функції , і справджується нерівність:

.

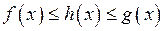Тоді, якщо функції і мають у точці одну й ту ж границю, тобто 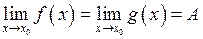, то у цій точці існує і границя функції 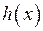, причому .

Доведення. З умови теореми маємо:

.

Або: .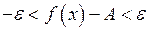

А також:

.

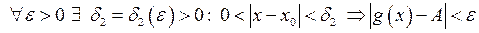Або: .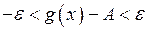

Позначимо: . Тоді в 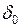-околі точки водночас будуть виконуватись нерівності:

.

Звідси в цьому околі виконано:

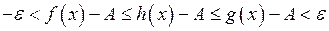, тобто . А це й означає, що .

Цю теорему іноді називають теоремою «про двох поліцейських». І ось чому. Якщо два поліцейських беруть з двох сторін злодія, а потім обидва поліцейські йдуть в одному й тому ж напрямі, то у тому ж напрямі рухається і злодій. Функції і – «поліцейські», а функція 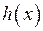– «злодій».

Використаємо цю теорему для встановлення наступного важливого співвідношення.

Дата добавления: 2015-05-24