Існування неявної функції, яка задається системою рівнянь

Існування неявної функції багатьох змінних

У цьому параграфі ми розглянемо узагальнення вище доведеної теореми для випадку функції двох змінних.

Теорема 2.1 Нехай М₀(х₀,у₀,z₀)ÎR³ і F(x,y,z) такі, що

1) F(x₀,y₀,z₀)=0;

2) в деякому околі точки М ₀, функція F(x,y,z) і F¢_x; F¢_y;F¢_z неперервні;

3) F¢_z(x₀,y₀,z₀)¹0.

Тоді в деякому паралелепіпеді П={ x,y,z: x₀-d ₁ <x<x₀+d ₁, y₀-d₂<y<y₀-d₂,

z₀-d₃<z<z₀+d₃ } рівняння F(x,y,z) визначатиме єдину функцію z=F(x,y), яка буде визначена в прямокутнику П₁={ (х,у): x₀-d ₁ <x<x₀+d ₁, y₀-d ₂ <y<y₀-d ₂}, яка буде неперервно диференційовною в цьому прямокутнику.

Частинні похідні будуть обчислюватися за формулами:

;

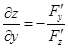
Аналогічна теорема має місце для випадку функції від більше ніж 3-х змінних.

Іноді буває, що неявні функції задаються системою рівнянь. При цьому має місце така теорема.

Теорема 3.1 Нехай маємо таку систему: 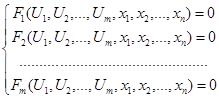(3.1)

і 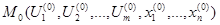– точка, координати якої задовільняють кожному рівнянню системи (3.1).

Тоді, якщо:

1) в деякому околі точки М ₀, існують всі часткові похідні першого порядку функцій F₁,…,F_m, при чому частинні похідні 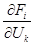, де 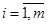; 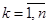, будуть неперервні в точці М₀;

2) величина, яка називається якобіяном і позначається

відмінна від нуля в точці М₀, то існують додатні числа e ₁ >0, e₂>0,…,e_m>0 та окіл точки 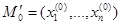такий, що в ньому існує єдиний набір функцій:

U ₁ =j ₁ (x ₁ ,…,x_n)

U₂=j₂(x ₁ ,…,x_n)

………………..

U_m=j₂(x₁,…,x_n),

які є розв’язками системи (3.1). В межах цього околу матимуть місце нерівності:

Кожна з функцій j_і є неперервною в цьому околі точки М¢₀ та диференційовною в ньому.

В зв’язку з цією теоремою виникає питання, а як же знайти частинні похідні від функцій j_і, які одержалися в попередній теоремі. Адже із формулювання зрозуміло, що теорема стверджує тільки існування тих функцій і не дає можливості їх явно задати. Отже, як знайти їх частинні похідні?

Для цього продиференціюємо кожне із рівнянь системи (3.1) по змінній х _1. Зважаючи на те, що х_і – незалежні змінні, а U_i – функції від х₁...х_п, матимемо:

……………………………………………

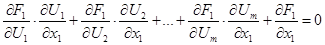
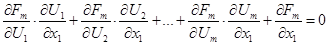
Ми одержимо систему m лінійних рівнянь відносно т невідомих 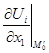. Головний визначник цієї системи це є якобіян, взятий в точці М₀, який за умовою теореми не дорівнює нулю.

Розв’язавши цю систему, ми знайдемо

Для того, щоб знайти частинні похідні по інших змінних зробимо те саме.

Дата добавления: 2015-05-24