Рекомендации по методике преподавания отдельных тем

Обсудим методические проблемы изложения различных тем, из которых может быть сконструировано изучение компьютерно­го моделирования. Введение в компьютерное моделирование целесообразно построить в виде лекции, содержащей в доступной учащимся форме обзор основных принципов абстрактного (по другой терминологии — информационного) моделирования во­обще и его реализации с помощью компьютеров. В итоге лекции учащиеся должны усвоить основополагающие знания о принци­пах моделирования, разновидностях компьютерного моделирова­ния, основных этапах компьютерного моделирования.

Этапы компьютерного моделирования показаны на рисунке, каждый из этих этапов требует обсуждения. Необходимо, чтобы учащиеся поняли, что, приступая к построению модели, прежде всего надо ответить на вопросы: для чего нужна модель? как мы будем ею пользоваться? В зависимости от ответов могут получить­ся совершенно разные модели одного и того же объекта.

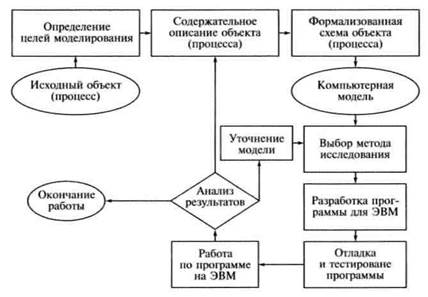
Добиться понимания этого можно в первую очередь на приме­рах из общ­еизвестных областей реальности. Сопоставим, напри­мер, три модели самолета: детская игрушка, натурная модель для испытания в аэродинамической трубе и абстрактная модель в виде чертежей. Все они имеют право на жизнь, но назначение у них принципиально различное. Далее, могут быть и различные цели, приводящие к построению нескольких различных абстрактных моделей для последующего компьютерного моделирования: на­пример, задачи, решаемые авиаконструктором, мало похожи на задачи, решаемые экономистом, которого заботит стоимость из­делия, рентабельность производства и т.п.

Содержательное описание объекта (процесса) служит основой дли дальнейшей формализации. Формализованная схема является промежуточным звеном между содержательным описанием и мо­делью и разрабатывается тогда, когда из-за сложности исследу­емого процесса непосредственный переход от содержательного описания к модели затруднен.

Технология компьютерного математического моделирования. В рамках физико-математического профиля, в котором изучение моделирования играет особо важную роль, ведущее значение при­надлежит компьютерному математическому моделированию. Особая роль темы заключается в том, что в ней повторя­ются и обобщаются основные понятия КММ, известные из базо­вого курса информатики, вводятся новые понятия: «моделирова­ние», «информационное моделирование», «математическое мо­делирование», «формализация», «идентификация модели» и др.

Другой важный аспект темы — формирование представления об этапах компьютерного математического моделирования. Здесь, с одной стороны, фигурируют приведенные выше понятия, с дру­гой стороны, присутствует полная технологическая цепочка КММ. Конечно, все эти этапы будут неоднократно повторяться при ис­следовании конкретных процессов (объектов), но основы закла­дываются именно на вводных занятиях. Действительно, одним из условий успешного усвоения учащимися систематического изуче­ния КММ является наличие у них хорошо развитых представле­ний об этапах КММ, значении каждого из этапов.

При обсуждении этапов КММ можно использовать общую схему абстрактного моделирования, изображенную на рисунке выше обсуж­дение следует конкретизировать с учетом особенностей именно математического моделирования.

Формализованная схема является промежуточным звеном между содержательным описанием и математической моделью и разра­батывается в тех случаях, когда из)за сложности исследуемого процесса переход от содержательного описания к математичес­кой модели оказывается невозможным. На этапе построения фор­мализованной схемы должна быть дана точная математическая задача исследования с указанием входных и выходных параметров модели. Важнейшим этапом моделирования является разделение входных параметров по степени важности влияния их изменений на выходные. Такой процесс называется ранжированием. Чаше все­го невозможно, да и не нужно, учитывать все факторы, которые могут повлиять на значения выходных параметров, отбрасывание менее значимых факторов огрубляет объект моделирования и спо­собствует пониманию его главных свойств и закономерностей.

На этане перехода от формализованной схемы к математиче­ской модели необходимо перейти от абстрактной формулировки к формулировке, имеющей конкретное математическое наполнение. В этот момент модель предстает перед нами в виде уравнения, системы уравнений, неравенств, матриц, дифференциальных урав­нений и т.д.

В ходе изучения этой темы учащ­иеся должны уяснить подходы к классификации компьютерных математических моделей. В лите­ратуре используются классификации моделей по математическо­му аппарату, отраслям наук и т.д. Наиболее органичной представ­ляется классификация по целям моделирования. Действительно, выделение целей моделирования — это первое, что необходимо сделать перед содержательным описанием и формализацией объек­та (процесса), и, в конечном итоге, именно цели моделирования определяют, какая модель будет построена. Учителю следует при­вести примеры постановки задач, приводящих к моделям, отно­сящ­имся к основным классам: дескриптивным, оптимизацион­ным, многокритериальным, игровым, имитационным.

Моделирование физических процессов. Эта тема фигурирует почти во всех вариантах изучения компьютерного математическо­го моделирования. Причина - традиции и относительная просто­та решаемых задач, их близость школьному курсу физики.

Целесообразно предпослать обсуждению вводную лекцию (бе­седу) о компьютерном моделировании физических процессов в целом. Вначале на ряде примеров иллюстрируем утверждение, что физика — наука, в которой математическое моделирование явля­ется чрезвычайно важным методом исследования.

Перечень рассматриваемых вопросов может быть таков:

· движение тел с учетом сопротивления среды;

· движение маятника с учетом сопротивления среды, вынуж­денные колебания, резонанс и т.д.;

· движение небесных тел (задача двух тел);

· движение заряженных частиц и др.

При моделировании движения тела, прежде всего, целесооб­разно рассмотреть традиционные для школьного курса физики динамические модели, но с учетом сопротивления среды. Это сво­бодное падение тела, полет тела, брошенного под углом к гори­зонту, движение тела с переменной массой. При этом составля­ющие силы сопротивления можно рассмотреть предварительно, перед изучением конкретных моделей, либо в ходе построения одной из моделей.

Более детально обсудим методику построения компьютерных математических моделей физических процессов и их последующего исследования на примере нескольких задач.

Первая из них - моделирование свободного паления тела с учетом сопротивления среды. Основная дидактическая роль этой задачи — практическое знакомство с этапами компьютерного математического моделирования, освоение этих этапов, приоб­ретение навыков формулирования и разрешения учебных проблем, проблемных ситуаций. Несмотря на то, что, на первый взгляд, она является простой, при ее исследовании придется решить ряд серьезных проблем, о которых будет говориться далее.

В ходе обучения неизбежно придется пользоваться понятиями «предел» и «производная». Понятие «предел» не вызывает су­ще­ственных затруднений; в контексте данного обсуждения вполне достаточно интуитивного понимания предела, сформированного у учащихся к X кл.

Не совсем так обстоит дело с понятием «производная». Воз­можны две ситуации:

1) уча­щиеся вполне им владеют и дифференциальная форма записи второго закона Ньютона (и последующ­их при решении конкретных задач дифференциальных уравнений) понятна: при этом никакой техники дифференцирования и тем более решения дифференциальных уравнений не требуется;

2) учащ­иеся не знакомы с этим понятием; в этом случае необ­ходимо сделать математическое отступление и пояснить понятие «производная», для этого, как показывает опыт, вполне доста­точно одного урока.

Другая методическая проблема, которую необходимо решить, — строить модели динамических процессов в виде дифференциаль­ных или конечно-разностных уравнений. Как показывает практи­ка, учащ­иеся физико-математических классов вполне способны воспринять дифференциальные уравнения и численные методы их решения. Для этого достаточно ввести дифференциальные урав­нения и объяснить простейшие численные методы их решения, базируясь на физическом и геометрическом смысле производной.

При изучении динамических процессов в менее подготовлен­ной аудитории рекомендуется ограничиться конечно-разностны­ми уравнениями. Любую модель такого рода можно сформулиро­вать в конечно-разностном виде, вообще не упоминая о диффе­ренциальных уравнениях.

Отметим, что сущ­ествует немало компьютерных программ, моделирующих простые физические процессы. В них реализован, в той или иной мере профессионально, диалоговый интерфейс, позволяю­щий вводить параметры, получать на экране таблицы, графики, движущ­иеся изображения. Однако при их использова­нии остаются скрытыми физические законы, определяющие про­цесс. ограничения модели, возможности ее усовершенствования. Такие программы полезны скорее как иллюстративные.

При выполнении компьютерной лабораторной работы по ис­следованию модели можно предложить учебные задания двух уров­ней (рассчитанные соответственно на «среднего» и «сильного» ученика):

I) получение результатов и их графическое отображение для заданного набора параметров модели;

2) исследование свободного падения тела в средах различной вязкости и содержательное сравнение результатов исследования;

3) придать модели черты оптимизационной (самостоятельно или с помощью учителя), выполнить указанные исследования, пронести содержательное сравнение результатов исследования.

По использованной здесь схеме могут вводиться и исследоваться другие модели, где учитывается сопротивление среды.

Имитационные стохастические модели. Имитационное модели­рование может стать су­щественной частью профильного курса информатики, включающего в себя изучение моделирования. Включение метода имитационного компьютерного моделирова­ния в профильный курс, работа учащ­ихся с имитационными мо­делями средней сложности представляет несомненный интерес и пользу, поскольку расширяет и обобщает представления о методе моделирования и его возможностях.

Идея имитационного моделирования интуитивно ясна и при­влекательна. В основе этого метода - теория вычислительных си­стем, статистика, теория вероятностей.

Начало изучения — лекция об имитационном моделировании случайных процессов. Один из вариантов отработки навыков ими­тационного стохастического моделирования — рассмотрение за­дачи моделирования очереди в системе массового обслуживания. Указанные системы элементарны для понимания постановки за­дач. имеют широкое прикладное значение.

Начать рассмотрение этой задачи целесообразно с обсуждения истории решения проблем массового обслуживания (задача Эрланга об обслуживании запросов на телефонной станции). Затем следует обзор типичных задач этой науки, после чего переход к рассмотрению простейшей задачи, которую можно сформулиро­вать на примере формирования и обслуживания очереди в мага­зине с одним продавцом. В этот магазин случайным образом вхо­дят покупатели. Если продавец свободен, то он начинает обслу­живать покупателя сразу, иначе покупатель становится в очередь. Детали постановки и решения этой задачи методом статистиче­ского моделирования можно найти в учебной литературе.

Обращаем внимание учащихся на то, какие вопросы ставятся в первую очередь при моделировании систем такого вида? Во-первых, это вычисление средних значений (математических ожи­даний) некоторых случайных величин. Например, какое среднее время приходится стоять в очереди к прилавку? Или: найти сред­нее время, проведенное продавцом в ожидании покупателя.

Задача учителя, в частности, состоит в том, чтобы разъяснить, что выборочные средние сами по себе — случайные величины; в другой выборке того же объема они будут иметь другие значения (при больших объемах выборки — не слишком отличающ­иеся друг от друга). Далее возможны варианты: в более подготовленной аудитории можно показать способ оценивания доверительных интер­валов, в которых находятся математические ожидания соответ­ствующих случайных величин при заданных доверительных веро­ятностях (известными из математической статистики методами без попытки обоснования). В еще более подготовленной в математи­ческом отношении аудитории можно ставить вопрос: каково рас­пределение случайных величин, являющихся результатами статистического моделирования, при заданных распределениях случай­ных величин, являющихся его входными параметрами? Посколь­ку изложение соответствующей математической теории в данном случае невозможно, следует ограничиться эмпирическими при­емами: построение гистограмм итоговых распределений и сравне­ние их с несколькими типичными функциями распределения.

На примере задачи об очереди отрабатываются сразу несколь­ко новых понятий и навыков:

· понятия о случайных процессах;

· понятия и простейшие навыки имитационного моделирова­ния;

· построение оптимизационных имитационных моделей;

· построение многокритериальных моделей (путем решения задач о наиболее рациональном обслуживании покупателей в со­четании с интересами владельца магазина).

Моделирование динамики развития популяций. Соответствующие модели достаточно просты и изучены, постановка их вполне оче­видна и в познавательном плане интересна и полезна.

Вводная беседа в этой теме может быть посвящ­ена введению в проблематику классической экологии и использование в ней ма­тематических моделей. Следует дать определения таким поняти­ям, как «популяция», «сообщество», «внутривидовая конкурен­ция*, «межвидовая конкуренция», сформулировать основные цели создания математических моделей в классической экологии.

При проведении беседы следует обратить внимание учащихся на то, что привлечение компьютеров су­щественно раздвинуло границы моделирования экологических процессов. С одной сторо­ны, появилась возможность всесторонней реализации сложных математических моделей, не допускающих аналитического иссле­дования, с другой стороны, возникли принципиально новые на­правления и, прежде всего, имитационное моделирование.

После вводной лекции приступаем к построению и исследова­нию конкретных моделей. Методически уместно начать это с рас­смотрения развития популяций с дискретным размножением, после чего следует плавный переход на популяции с непрерыв­ным размножением. Естественная последовательность рассмотре­ния такова:

· динамическое моделирование численности изолированной популяции с дискретным размножением:

а) при отсутствии внутривидовой конкуренции;

б) при наличии внутривидовой конкуренции;

· динамическое моделирование численности изолированной популяции с непрерывным размножением:

а) при отсутствии в и угри видовой конкуренции;

б) при наличии внутривидовой конкуренции;

· динамическое моделирование взаимодействия популяций:

а) состоящих в отношениях межвидовой конкуренции;

б) состоящих в отношениях «хищник—жертва»;

· имитационное моделирование развития популяции и взаимо­действия популяций.

Есте­ственной частью этой темы является также работа с имитацион­ными моделями экологических процессов (например, типа «хищ­­ник—жертва»).

Инструментарий компьютерного математического моделирова­ния. Компьютерная реализация моделей с учетом обсуждаемого профиля может быть реализована:

· путем создания программ на традиционных языках програм­мирования (Паскаль, Бейсик и других, а также их современные версии - Delphi, Visual Basic for Application и т.п.);

· с помощью табличных процессоров;

· с помощью специальных пакетов прикладных программ для решения математических задач (MathCAD и т.п.).

Каждый из способов имеет свои методические достоинства и недостатки. При реализации темы «Компьютерное математическое моделирование» в объеме, соответствующем физико-математи­ческому профилю (т.е. достаточно большом), используются, как правило, хотя бы два из указанных способов.

Поскольку программирование является наряду с моделирова­нием ключевой темой данного профиля, привлечение его в каче­стве инструмента представляется необходимым. В процессе про­граммирования учащимся становятся доступными детали матема­тических процедур; более того, они просто вынуждены их осваи­вать, что работает на общую цель данного профиля.

В результате изучения раздела «Моделирование» в профильном курсе информатики учащиеся должны:

· знать (понимать): виды и свойства информационных моде­лей реальных объектов и процессов, методы и средства компь­ютерной реализации информационных моделей; общую структу­ру деятельности по созданию компьютерных моделей;

· уметь: выделять информационный аспект в деятельности че­ловека; информационное взаимодействие в простейших соци­альных, биологических и технических системах; строить инфор­мационные модели объектов, систем и процессов, используя для этого типовые средства (язык программирования, таблицы, графики, диаграммы, формулы и т.п.): интерпретировать результа­ты, получаемые в ходе моделирования реальных процессов; про­водить виртуальные эксперименты и самостоятельно создавать простейшие модели в учебных виртуальных лабораториях и моде­лирующих средах;

· использовать приобретенные знания и умения в практической деятельности и повседневной жизни: для расширения представле­ния о моделировании как универсальном методе научного позна­ния объектов, процессов и явлении реального мира, формирова­ния компетенции в сфере познавательной деятельности¹.

Дата добавления: 2015-05-08