Энтропия

Самопроизвольные и несамопроизвольные процессы.

Направление самопроизвольного протекания процессов. Второе начало термодинамики.

1) самопроизвольные процессы, протекание которых не требует затрат энергии извне; с их помощью можно получить работу

2) несамопроизвольные процессы, для проведения которых необходимо затратить энергию или совершить работу.

Для любого процесса важно установить критерий, определяющий возможность его самопроизвольного протекания в данных условиях. Первый закон термодинамики такого критерия не дает, в действительности возможно самопроизвольное протекание как экзо-, так и эндотермических процессов, например:

NH₄NO₃ (к) ® NH₄NO₃ (р) DH > 0

CaCl₂ (к) ® CaCl₂ (р) D H < 0

Таким образом, знак теплового эффекта процесса не определяет однозначно возможность его самопроизвольного протекания.

Второй закон термодинамики позволяет установить возможность и пределы самопроизвольного протекания процесса, а также определить, какая часть энергии системы может быть превращена в работу.

Рассмотрим процесс смешения двух инертных газов, для которого DH»0:

состояние 1 состояние 2

Очевидно, что переход системы из состояния 1 в состояние 2 происходит самопроизвольно, а самопроизвольное протекание обратного процесса невозможно. Энергия системы в обоих состояниях одинакова и не может быть движущей силой смешения газов. В то же время, в состоянии 2 система характеризуется большей степенью беспорядка, чем в состоянии 1. Кроме того, состояние 2 более вероятно, чем состояние 1, так как трудно представить, чтобы два газа, не разделенные перегородкой, не смешались. Следовательно, движущей силой процесса смешения газов является стремление системы перейти в состояние с большей степенью беспорядка, которое для любой системы является наиболее вероятным.

Таким образом, процессы, протекающие без изменения энергии системы, идут самопроизвольно в направлении наиболее вероятного состояния этой системы, т. е. состояния с наибольшей степенью беспорядка.

Для количественной оценки вероятности состояния системы используют понятие термодинамическая вероятность W. Термодинамическая вероятность состояния системы – это число микросостояний (число способов), с помощью которых может быть реализовано данное макросостояние системы. Макросостояние системы определяется температурой, давлением, объемом и другими параметрами состояния системы. Микрокросостояние системы складывается из мгновенных характеристик всех частиц, образующих систему (атомов, молекул и т.д.), – их координат, скорости движения, энергии. Каждому макросостоянию отвечает огромное число микросостояний. Для удобства расчетов в термодинамике используют величину, пропорциональную lnW, отнесенную к одному молю вещества:

S = RlnW,

где R- универсальная газовая постоянная [Дж/моль К].

Величину S называют энтропией системы и измеряют в Дж/моль К.

Энтропия является мерой беспорядка системы. Чем больше степень беспорядка в системе, тем выше ее энтропия. Состояние системы с большей энтропией (с большим беспорядком) более вероятны.

Таким образом, процессы, протекающие без изменения энергии системы, идут самопроизвольно в направлении увеличения энтропии системы.

Энтропия – это функция состояния системы. Ее изменение DS в процессе может быть рассчитано на основании закона Гесса и его следствий.

В отличие от внутренней энергии и энтальпии абсолютное значение энтропии поддается определению, так как она имеет нулевую точку отсчета.

Согласно третьему закону термодинамики:

Энтропия идеального кристалла при 0 К равняется нулю.

Энтропии веществ в стандартном состоянии 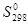[Дж/моль К] определены и приводятся в справочных таблицах.

Энтропия зависит от температуры, от агрегатного состояния вещества, от давления (для гозов).

Иногда знак изменения энтропии в процессе можно оценить без точных расчетов. Так, изменения энтропии вещества при плавлении и испарении положительны: DS_пл>0, DS_исп>0, причем DS_пл>DS_пл.

Знак DS в ходе химической реакции можно оценить, не прибегая к точным расчетам, только в том случае, если процесс сопровождается изменением числа молей газообразных веществ:

CaCO3(к) ® CaO(к) + CO2(г) DS>0

N2(г) + 3 H2(г) ® 2 NH3(г) DS<0

Дата добавления: 2015-05-09