Матрицы и графы. Нахождение путей и сечений с помощью структурной матрицы

Трудно переоценить роль матриц в теории графов (в частности, матрицы полезны, чтобы данный граф более “легко” воспринимался компьютером). Перечислим наиболее известные матрицы.

1. Матрица смежности. Это квадратная матрица порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р),то на главной диагонали в строчке с номером k стоит число р). Если вершина i связана с вершиной j однимребром, то элемент матрицы смежности a_ij равен 1, если эти вершинысвязаны s ребрами, то а_ij= s. Аналогичным образом строятся матрицы смежности для орграфов и для мультиграфов.

Легко видеть, что матрица В =А ² = АА составлена из целых чисел b_ij,которые равны числу путей длины 2, соединяющих вершины i и j. Понятно, что А ³составлена из чисел, равных числу путей длины 3 (т. е. путей из 3-х ребер) из вершины i ввершину j и т. д.

1. Матрица инциденций – это матрица размера n ´ m,где n – число вершин, а m – число ребер графа, при этом ее элементы k_ij равны 1, если вершина с номером i является для ребра с номером j начальной или конечной (если ребро неориентировано) и начальной для ориентированных ребер. Заметим, что матрица инциденций сравнительно редко используется, так как в современных условиях (где число ребер часто очень велико) она имеет слишком большое число столбцов.
2. Структурная матрица. Именно эта матрица имеет особое значение в теории сетей связи. Структурная матрица – это символьная матрица порядка п. Она составляется следующим образом: на главной диагонали стоит 1, т. е. a_ii = 1, остальные элементы – это символьные обозначения ребер (если вершины i и j не соединены ребром, то a_ii = 0). При этом, если при i < j вершины i и j соединены ребром а, то элемент s_ij = a,при i>j – это отрицание а, которое обычно отмечается чертой сверху. Если связи вершины i c вершиной j нет, то соответствующий элемент равен 0, структурная матрица может составляться и для орграфа и для мультиграфа без петель (здесь если дваребра а и b соединяют две вершины, то соответствующий элемент при i <j равен a Ú b,апри i>j этот элемент равен

Отметим, что в учебных целях, когда действия с матрицами осуществляются студентами “вручную” (число вершин в графе невелико), можно обозначать ребра латинскими буквами без индексов a, b, c и т. д., но при использовании компьютера гораздо удобнее обозначать ребра а (i,j), если это ребро соединяет вершины i и j при i<j и с чертой сверху, если i>j.

Теорема. Для того чтобы найти все пути (простые) из вершины i в вершину j достаточно раскрыть минор M (j, i) структурной матрицы методами булевой алгебры. При этом раскрытие минора производится обычными действиями с определителями, но при этом сложение заменяется дизъюнкцией, умножение – конъюнкцией, знаки умножения на числа не используются.

Подробно доказывать эту теорему не будем, но отметим, что определитель равен сумме (в данном случае дизъюнкции) элементов, взятых по одному из каждой строчки и каждого столбца с определенным знаком. В нашем случае знаки не присутствуют, а значит, любой член раскрытия определителя всей структурной матрицы S соответствует циклу в графе. Если же брать минор M (j,i),то его раскрытие соответствует тем членам определителя, в которых имелся элемент s (j,i),но безсамого этого элемента (таким образом, индексы i и j встречаютсявместо двух только один раз). Это и означает, что получаем маршрут от вершины с номером i к вершине с номером j.

Понятно, что раскрытие минора методами булевой алгебры предусматривает, что верны следующие соотношения: 1Ú a = 1, 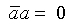(это свойство нужно, для того чтобы не проходить по одному ребру дважды в противоположных направлениях), а также используется правило простого поглощения (х Ú ху = х). Видно, что если не использовать правило поглощения, то получим все маршруты (без повторения ребер), связывающие вершины i и j.

Примечание. 1. Если граф не ориентирован, то миноры M (j,i)и M(i,j) совпадают.

2. После получения ответа, черточки над обозначениями ребер (т. е. отрицания) можно убрать (на самом деле “черта” над ребром означает, что ребро проходится от вершины с большим номером к вершине с меньшим номером). Затем рекомендуется записать каждый путь по порядку прохождения ребер (в этом случае удобны обозначения ребер с индексами вершин).

Сечением (разрезом) междувершинами i и j называется неизбыточный набор ребер, при удалении которых из графа теряется связь между данными вершинами (не существует пути из вершины i в вершину j). Заметим, что сечений между данными вершинами может быть много, и они могут содержать разное количество ребер.

Слово “неизбыточный” означает, что если любое ребро из сечения снова возвратить в граф, то связь восстановится.

Естественно, что если известны все пути из вершины i в вершину j, причем эти пути заданы в виде ДНФ, т. е. дизъюнктивной нормальной формы (а именно такой вид получается после раскрытия соответствующего минора структурной матрицы), то все сечения между этими вершинами можно получить отрицанием этих путей (по правилу де Моргана конъюнкцию заменить на дизъюнкцию и наоборот), затем полученное выражение снова привести к ДНФ, используя раскрытие скобок по обычным правилам, при этом правило поглощения обеспечит неизбыточность набора ребер в каждом сечении. Ясно, что знаки отрицания (черточки над символами ребер) можно опустить. Пример на эту тему приведен в разд. 15 (примеры решения типовых задач).

Дата добавления: 2015-05-09