Произвольные функции и логические схемы

Поскольку значениями логических функций могут быть только 0 или 1, то любые логические функции можно использовать как аргументы других логических функций, т.е. строить из простых функций более сложные. Пусть в таблице 1.2. задана произвольная функция Y трех аргументов, и ее нужно выразить с помощью простых функций НЕ, И, ИЛИ.

Очевидно, что Y = 1, когда или a 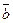c = 1 (строка 1), или (строка 3), или 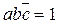(строка 6), или (строка 7).

Таблица 1.2.

№	Аргументы	Функция	№	Аргументы	Функция
	a	b	c	Y		a	b	c	Y

Все это можно записать в виде одного общего аналитического выражения: 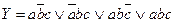(1.1)

Полученное аналитическое выражение называют совершенной дизъюнктивной нормальной формой (СДНФ). СДНФ состоит из элементарных конъюнкций, соединенных знаками дизъюнкций. Конъюнкцию называют элементарной, если в нее не входит по несколько одинаковых букв. Число элементарных конъюнкций в СДНФ обязательно равно числу единичных значений функции в таблице истинности. В каждую элементарную конъюнкцию СДНФ входят обязательно все аргументы функции в прямой или инверсной форме.

Поскольку процедуру построения СДНФ в принципе можно применить к таблице, содержащей любое число аргументов при любом расположении единичных значений функции, то можно сделать важный вывод: с помощью набора функций НЕ, И, ИЛИ можно выразить любую логическую функцию. Такой полный набор называют логическим базисом или просто базисом.

Нетрудно показать, что базисами являются также и другие наборы:

НЕ, И; НЕ, ИЛИ; И-НЕ и ИЛИ-НЕ.

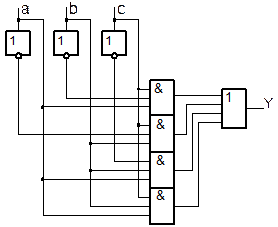Для построения логической схемы, реализующей функцию, заданную таблицей истинности, обычно удобнее аналитическая форма представления функции. В данном случае - это выражение (1.1). Схема, реализующая (1.1), показана на рис. 1.6. Она состоит из трех ярусов. В первом ярусе расположены инверторы. Очевидно, что максимальное число инверторов не превышает числа аргументов. Во втором ярусе расположены элементы И, реализующие входящие в формулу элементарные конъюнкции. Число входов каждого элемента равно числу аргументов реализуемой функции, а число элементов- числу элементарных конъюнкций в формуле. В третьем ярусе схемы стоит элемент ИЛИ, число входов которого равно числу дизъюнкций в формуле.

Рис.1.6. Логическая схема, реализующая (1.1).

Дата добавления: 2015-05-09