
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы поиска по дереву
Лекция 82. Методы организации индексов
Существуют два класса методов, реализующих доступ к данным по ключу:
методы поиска по дереву,
методы хеширования.
Определение: Деревом называется конечное множество, состоящее из одного или более элементов, называемых узлами, таких, что:
между узлами имеет место отношение типа "исходный-порожденный";
есть только один узел, не имеющий исходного. Он называется корнем;
все узлы за исключением корня имеют только один исходный; каждый узел может иметь несколько порожденных;
отношение "исходный-порожденный" действует только в одном направлении, т.е. ни один потомок некоторого узла не может стать для него предком.
Число порожденных отдельного узла (число поддеревьев данного корня) называется его степенью. Узел с нулевой степенью называют листом или концевым узлом. Максимальное значение степени всех узлов данного дерева называется степенью дерева.
Если в дереве между порожденными узлами, имеющими общий исходный, считается существенным их порядок, то дерево называется упорядоченным. В задачах поиска почти всегда рассматриваются упорядоченные деревья.
Упорядоченное дерево, степень которого не больше 2 называется бинарным деревом. Бинарное дерево особенно часто используется при поиске в оперативной памяти. Алгоритм поиска: вначале аргумент поиска сравнивается с ключом, находящимся в корне. Если аргумент совпадает с ключом, поиск закончен, если же не совпадает, то в случае, когда аргумент оказвается меньше ключа, поиск продолжается в левом поддереве, а в случае когда больше ключа - в правом поддереве. Увеличив уровень на 1 повторяют сравнение, считая текущий узел корнем.
Пример*: Пусть дан список студентов, содержащий их фамилии средний бал успеваемости (см. таблицу 1.1). В качестве ключа используется фамилия студента. Предположим, что все записи имеют фиксированную длину, тогда в качестве указателя можно использовать номер записи. Смещение записи в файле в этом случае будет вычислятся как ([номер_записи] -1) * [длина_записи] . Пусть аргумент поиска "Петров". На рисунке 1.2 показаны одно из возможных для этого набора данных бинарных деревьев поиска и путь поиска.
| Таблица 1.1. | |
| Студент | Балл |
| Васильев | 4,2 |
| Иванов | 3,4 |
| Кузнецов | 3,5 |
| Петров | 3,2 |
| Сидоров | 4,6 |
| Тихомиров | 3,8 |

Рис. 1.2.Поиск по бинарному дереву.
Заметим, что здесь используется следующее правило сравнения строковых переменных: считается, что значение символа соответствует его порядковому номеру в алфавите. Поэтому "И" меньше "К", а "К" меньше "С". Если текущие символы в сравниваемых строках совпадают, то сравниваются символы в следующих позициях.
Бинарные деревья особенно эффективны в случае когда множество ключей заранее неизвестно, либо когда это множество интенсивно изменяется. Очевидно, что при переменном множестве ключей лучше иметь сбалансированное дерево.
Определение: Бинарное дерево называют сбалансированным (balanced), если высота левого поддерева каждого узла отличается от высоты правого поддерева не более чем на 1.
При поиске данных во внешней памяти очень важной является проблема сокращения числа перемещений данных из внешней памяти в оперативную. Поэтому, в данном случае по сравнению с бинарными деревьями более выгодными окажутся сильно ветвящиеся деревья - т.к. их высота меньше, то при поиске потребуется меньше обращений к внешней памяти. Наибольшее применение в этом случае получили В-деревья (В - balanced)
Определение: В-деревом порядка n называется сильно ветвящееся дерево степени 2n+1, обладающее следующими свойствами:
Каждый узел, за исключением корня, содержит не менее n и не более 2n ключей.
Корень содержит не менее одного и не более 2n ключей.
Все листья расположены на одном уровне.
Каждый нелистовой узел содержит два списка: упорядоченный по возрастанию значений список ключей и соответсвующий ему список указателей (для листовых узлов список указателей отсутствует).
Для такого дерева:
сравнительно просто может быть организован последовательный доступ, т.к. все листья расположены на одном уровне;
при добавлении и изменении ключей все изменения ограничиваются, как правило, одним узлом.

Рис. 1.3.Сбалансированное дерево.
В -дерево, в котором истинные значения содержатся только в листьях (концевых узлах), называется В+ -деревом. Во внутренних узлах такого дерева содержатся ключи-разделители, задающие диапазон изменения ключей для поддеревьев.
Наиболее популярным подходом к организации индексов в базах данных является использование техники B-деревьев. С точки зрения физической организации B-дерево представляется как мультисписочная структура страниц внешней памяти, т.е. каждому узлу дерева соответствует блок внешней памяти (страница). Внутренние и листовые страницы обычно имеют разную структуру.
В типовом случае структура внутренней страницы выглядит следующим образом:

При этом выдерживаются следующие свойства:
ключ(1) <= ключ(2) <=... <= ключ(n);
в странице дерева Nm находятся ключи k со значениями ключ(m) <= k <= ключ(m+1).
Листовая страница обычно имеет следующую структуру:
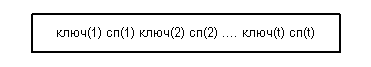
Листовая страница обладает следующими свойствами:
ключ(1) < ключ(2) <... < ключ(t);
сп(r) - упорядоченный список идентификаторов кортежей (tid), включающих значение ключ(r);
листовые страницы связаны одно- или двунаправленным списком.
Поиск в B-дереве - это прохождение от корня к листу в соответствии с заданным значением ключа. Заметим, что поскольку деревья сильно ветвистые и сбалансированные, то для выполнения поиска по любому значению ключа потребуется одно и то же (и обычно небольшое) число обменов с внешней памятью. Более точно, в сбалансированном дереве, где длины всех путей от корня к листу одни и те же, если во внутренней странице помещается n ключей, то при хранении m записей требуется дерево глубиной logn(m), где logn вычисляет логарифм по основанию n. Если n достаточно велико (обычный случай), то глубина дерева невелика, и производится быстрый поиск.
Основной "изюминкой" B-деревьев является автоматическое поддержание свойства сбалансированности.
82.1.1. Автоматическое поддержание свойства сбалансированности B-деревьев при выполнении операций занесения и удаления записей *
При занесении новой записи выполняется:
Поиск листовой страницы. Фактически, производится обычный поиск по ключу. Если в B-дереве не содержится ключ с заданным значением, то будет получен номер страницы, в которой ему надлежит содержаться, и соответствующие координаты внутри страницы.
Помещение записи на место. Естественно, что вся работа производится в буферах оперативной памяти. Листовая страница, в которую требуется занести запись, считывается в буфер, и в нем выполняется операция вставки. Размер буфера должен превышать размер страницы внешней памяти.
Если после выполнения вставки новой записи размер используемой части буфера не превосходит размера страницы, то на этом выполнение операции занесения записи заканчивается. Буфер может быть немедленно вытолкнут во внешнюю память, или временно сохранен в оперативной памяти в зависимости от политики управления буферами.
Если же возникло переполнение буфера (т.е. размер его используемой части превосходит размер страницы), то выполняется расщепление страницы. Для этого запрашивается новая страница внешней памяти, используемая часть буфера разбивается грубо говоря пополам (так, чтобы вторая половина также начиналась с ключа), и вторая половина записывается во вновь выделенную страницу, а в старой странице модифицируется значение размера свободной памяти. Естественно, модифицируются ссылки по списку листовых страниц.
Чтобы обеспечить доступ от корня дерева к заново заведенной страницы, необходимо соответствующим образом модифицировать внутреннюю страницу, являющуюся предком ранее существовавшей листовой страницы, т.е. вставить в нее соответствующее значение ключа и ссылку на новую страницу. При выполнении этого действия может снова произойти переполнение теперь уже внутренней страницы, и она будет расщеплена на две. В результате потребуется вставить значение ключа и ссылку на новую страницу во внутреннюю страницу-предка выше по иерархии и т.д.
Предельным случаем является переполнение корневой страницы B-дерева. В этом случае она тоже расщепляется на две, и заводится новая корневая страница дерева, т.е. его глубина увеличивается на единицу.
При удалении записи выполняются следующие действия:
Поиск записи по ключу. Если запись не найдена, то значит удалять ничего не нужно.
Реальное удаление записи в буфере, в который прочитана соответствующая листовая страница.
Если после выполнения этой подоперации размер занятой в буфере области оказывается таковым, что его сумма с размером занятой области в листовых страницах, являющихся левым или правым братом данной страницы, больше, чем размер страницы, операция завершается.
Иначе производится слияние с правым или левым братом, т.е. в буфере производится новый образ страницы, содержащей общую информацию из данной страницы и ее левого или правого брата. Ставшая ненужной листовая страница заносится в список свободных страниц. Соответствующим образом корректируется список листовых страниц.
Чтобы устранить возможность доступа от корня к освобожденной странице, нужно удалить соответствующее значение ключа и ссылку на освобожденную страницу из внутренней страницы - ее предка. При этом может возникнуть потребность в слиянии этой страницы с ее левым или правыми братьями и т.д.
Предельным случаем является полное опустошение корневой страницы дерева, которое возможно после слияния последних двух потомков корня. В этом случае корневая страница освобождается, а глубина дерева уменьшается на единицу.
Как видно, при выполнении операций вставки и удаления свойство сбалансированности B-дерева сохраняется, а внешняя память расходуется достаточно экономно.
Проблемой является то, что при выполнении операций модификации слишком часто могут возникать расщепления и слияния. Чтобы добиться эффективного использования внешней памяти с минимизацией числа расщеплений и слияний, применяются более сложные приемы, в том числе:
упреждающие расщепления, т.е. расщепления страницы не при ее переполнении, а несколько раньше, когда степень заполненности страницы достигает некоторого уровня;
переливания, т.е. поддержание равновесного заполнения соседних страниц;
слияния 3-в-2, т.е. порождение двух листовых страниц на основе содержимого трех соседних.
Следует заметить, что при организации мультидоступа к B-деревьям, характерного при их использовании в СУБД, приходится решать ряд нетривиальных проблем. Конечно, грубые решения очевидны, например монопольный захват B-дерева на все выполнение операции модификации. Но существуют и более тонкие решения, рассмотрение которых выходит за пределы нашего курса.
|
|
Дата добавления: 2015-05-09; Просмотров: 358; Нарушение авторских прав?; Мы поможем в написании вашей работы!