
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вказівки та зразки розв’язування задач. 3 страница
|
|
|
|
Сталу записали у вигляді  для зручності спрощень. Далі маємо
для зручності спрощень. Далі маємо 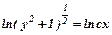 ;
;  ;
; 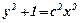 . Одержали загальний інтеграл рівняння.
. Одержали загальний інтеграл рівняння.
б)  ;
; 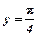 при
при 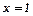 . Дане дифрівняння однорідне, оскільки
. Дане дифрівняння однорідне, оскільки  є функція від
є функція від  . Використаємо заміну
. Використаємо заміну 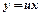 . Тоді
. Тоді  . Підставивши в дане рівняння, маємо
. Підставивши в дане рівняння, маємо 



 ;
; 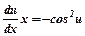 . Розділивши змінні, одержимо
. Розділивши змінні, одержимо  . Проінтегрувавши, дістанемо
. Проінтегрувавши, дістанемо  ;
; 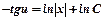 ;
; 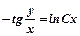 або
або 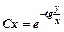 . Це загальний інтеграл даного рівняння.
. Це загальний інтеграл даного рівняння.
Підставивши початкові умови, знайдемо 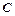 :
: 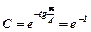 .
.
При такому С маємо розв’язок задачі Коші, що задовільняє даній умові:  або
або  .
. 
в)  . Розв’яжемо це рівняння методом Бернуллі. Це є лінійне неоднорідне рівняння першого порядку.
. Розв’яжемо це рівняння методом Бернуллі. Це є лінійне неоднорідне рівняння першого порядку.
Робимо заміну  , (1)
, (1) 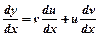 ;
; 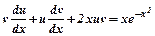 ;
;  (2);
(2);
Прирівнюємо до нуля вираз в дужках  .
.
Розв’язуємо диференціальне рівняння: 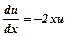 ;
;  ;
;  ,
,  ;
;  ; (3)
; (3)
Розв’язок підставимо в рівняння (2):  .
.
Розв’язуємо одержане рівняння: 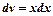 ;
; 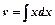 ,
, 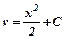 (4);
(4);
Підставивши (3)і (4)в (1), одержимо загальний розв’язок рівняння:
 .
.
г)  . Складаємо характеристичне рівняння
. Складаємо характеристичне рівняння
 ,
,
Корені дійсні різні.
Частинні незалежні розв’язки 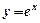 і
і 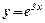 .
.
Загальний розв’язок  .
.
д) 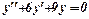 .
.
Характеристичне рівняння: 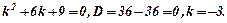
Рівняння має кратний корінь.
Незалежні частинні розв’язки -  і
і 
Загальний розв’язок даного рівняння 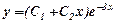 . Для знаходження частинного розв’язку знайдемо похідну
. Для знаходження частинного розв’язку знайдемо похідну
 .
.
Підставивши початкові умови, знайдемо 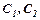 :
:

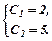
Підставляємо знайдені значення  в загальний розв’язок рівняння:
в загальний розв’язок рівняння:
 - це є шуканий розв’язок задачі Коші.
- це є шуканий розв’язок задачі Коші.
е)  .
.
1. Шукаємо  , який є загальним розв’язком однорідного рівняння
, який є загальним розв’язком однорідного рівняння 
Характеристичне рівняння - 
Корені комплексно спряжені: 
Частинні незалежні дійсні розв’язки: 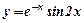 і
і 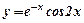 .
.
Загальний розв’язок -  .
.
2. Шукаємо 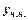 , який є частковим розв’язком неоднорідного рівняння
, який є частковим розв’язком неоднорідного рівняння  у вигляді
у вигляді 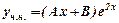 .
.
Разом з першою похідною
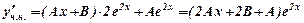 і другою похідною
і другою похідною 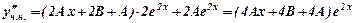 підставимо їх значення в задане неоднорідне рівняння
підставимо їх значення в задане неоднорідне рівняння
 Оскільки
Оскільки 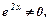 то скоротивши, отримаємо
то скоротивши, отримаємо
|
|
|
 і згрупувавши коефіцієнти біля степенів х, отримаємо
і згрупувавши коефіцієнти біля степенів х, отримаємо  .
.
Прирівнявши коефіцієнти біля однакових степенів х, маємо систему:
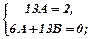
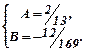
Частковий розв’язок  , тоді загальний розв’язок заданого неоднорідного рівняння такий:
, тоді загальний розв’язок заданого неоднорідного рівняння такий:

є)  .
.
1. Шукаємо  , який є загальним розв’язком однорідного рівняння
, який є загальним розв’язком однорідного рівняння 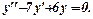
Характеристичне рівняння - 


Частинні незалежні розв’язки: 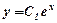 і
і 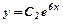 .
.
Загальний розв’язок -  .
.
2. Шукаємо 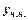 , який є частковим розв’язком неоднорідного рівняння
, який є частковим розв’язком неоднорідного рівняння  у вигляді
у вигляді  . Разом з першою похідною
. Разом з першою похідною 
 і другою похідною
і другою похідною  підставимо їх значення в задане неоднорідне рівняння
підставимо їх значення в задане неоднорідне рівняння
 або
або
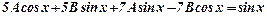 . Згрупувавши коефіцієнти біля sinx і cosx,отримаємо систему:
. Згрупувавши коефіцієнти біля sinx і cosx,отримаємо систему:
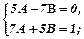
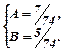
Отже, частковий розв’язок  , тоді загальний розв’язок заданого неоднорідного рівняння такий:
, тоді загальний розв’язок заданого неоднорідного рівняння такий:
 .
.
ж)  .
.
1. Шукаємо  , який є загальним розв’язком однорідного рівняння
, який є загальним розв’язком однорідного рівняння 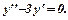
Характеристичне рівняння -  ,
, 
Частинні незалежні дійсні розв’язки:  і
і  .
.
Загальний розв’язок - 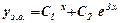 .
.
2. Шукаємо 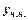 , який є частковим розв’язком неоднорідного рівняння
, який є частковим розв’язком неоднорідного рівняння 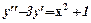 у вигляді
у вигляді  ,оскільки
,оскільки 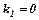 є простим коренем характеристичного рівняння. Разом з першою похідною
є простим коренем характеристичного рівняння. Разом з першою похідною 
 і другою похідною
і другою похідною  підставимо їх значення в задане неоднорідне рівняння
підставимо їх значення в задане неоднорідне рівняння
 або
або
 . Згрупувавши коефіцієнти біля степенів х, отримаємо систему:
. Згрупувавши коефіцієнти біля степенів х, отримаємо систему:


Отже, частковий розв’язок  , тоді, загальний розв’язок заданого неоднорідного рівняння такий:
, тоді, загальний розв’язок заданого неоднорідного рівняння такий:

21. Дослідити на збіжність ряди:
а) за ознакою Даламбера ряд 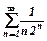 ;
;
б) за ознакою Коші ряди 1) 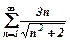 ; 2)
; 2)  ;
;
в) за ознакою порівняння ряди 1) 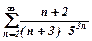 ; 2)
; 2)  ;
;
г) на умовну та абсолютну збіжність 1) 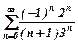 ; 2)
; 2)  .
.
Розв’язування.
а) застосуємо ознаку Даламбера до ряду 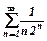 . В нас
. В нас 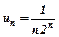 ,
,  .
.
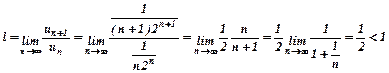 . Оскільки
. Оскільки 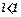 ,то даний ряд збіжний.
,то даний ряд збіжний.
б) застосуємо інтегральну ознаку Коші до рядів:
1) 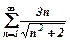 . Обчислимо інтеграл
. Обчислимо інтеграл 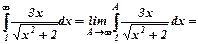
{ заміна:  }
}
 .
.
Інтеграл розбіжний, значить даний ряд теж розбіжний.
2) 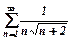 .
.
Обчислимо інтеграл 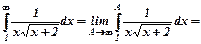
{ заміна: 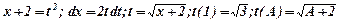 }
}
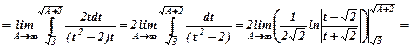
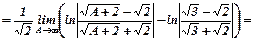
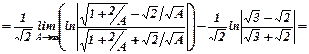
 Інтеграл збіжний, отже, і ряд теж збіжний.
Інтеграл збіжний, отже, і ряд теж збіжний.
в) для рядів  і
і 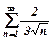 використаємо ознаку порівняння:
використаємо ознаку порівняння:
1)  . Оскільки для всіх
. Оскільки для всіх 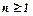 :
:  , то
, то  , при
, при 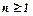 .
.
|
|
|
Ряд 
 є збіжний тому, що це є ряд геометричної прогресії зі знаменником
є збіжний тому, що це є ряд геометричної прогресії зі знаменником 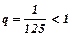 . Тоді за ознакою порівняння збіжний і даний ряд.
. Тоді за ознакою порівняння збіжний і даний ряд.
2) 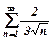 . Оскільки для всіх
. Оскільки для всіх 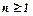 :
: 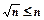 , то
, то 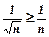 . Гармонійний ряд
. Гармонійний ряд 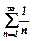 розбіжний (за інтегральною ознакою Коші), і отже, ряд
розбіжний (за інтегральною ознакою Коші), і отже, ряд  - теж розбіжний. А даний ряд
- теж розбіжний. А даний ряд  також розбіжний.
також розбіжний.
1) Ряд  знакопереміжний. За ознакою Даламбера дослідимо ряд, складений з абсолютних величин. Визначаємо:
знакопереміжний. За ознакою Даламбера дослідимо ряд, складений з абсолютних величин. Визначаємо:  =
=
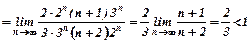
Значить, даний ряд збіжний. Отже, заданий знакопереміжний ряд є абсолютно збіжним.
2)  .
.
За інтегральною ознакою Коші дослідимо ряд, складений з абсолютних величин. Обчислимо інтеграл 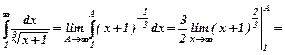
 Отже, даний ряд розбіжний.
Отже, даний ряд розбіжний.
Заданий знакопереміжний ряд дослідимо за ознакою Лецбніца:.
1)  - члени ряду за абсолютною величиною утворюють спадну числову послідовність; 2)
- члени ряду за абсолютною величиною утворюють спадну числову послідовність; 2)  .
.
Значить, заданий знакопереміжний ряд є умовно збіжний..
22. Знайти інтервал збіжності степеневого ряду 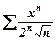 і дослідити збіжність на кінцях інтервалу.
і дослідити збіжність на кінцях інтервалу.
Розв’язування. В даному випадку
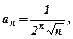
 .
.
Знаходимо радіус збіжності ряду
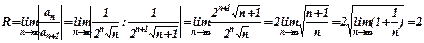 В інтервалі
В інтервалі 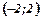 ряд збігається абсолютно.
ряд збігається абсолютно.
Дослідимо збіжність степеневого ряду в точці 
Ряд 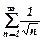 дослідимо за ознакою Коші.
дослідимо за ознакою Коші.
 .
.
Значить, даний ряд розбіжний.
При  одержимо знакопереміжний ряд
одержимо знакопереміжний ряд
 який дослідимо за ознакою Лейбніца:
який дослідимо за ознакою Лейбніца:
1). 1> 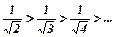 - спадна числова послідовність;
- спадна числова послідовність;
2).  .
.
Отже, за ознакою Лейбніца даний знакозмінний ряд збігається.
Таким чином, степеневий ряд збігається в півінтервалі 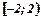 ; на лівому кінці збігається умовно, а на правому розбігається.
; на лівому кінці збігається умовно, а на правому розбігається.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 904; Нарушение авторских прав?; Мы поможем в написании вашей работы!