
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Умовний екстремум 2 страница
|
|
|
|
Пример. Практически одна и та же случайно отобранная совокупность объектов — коммерческих банков одного административного округа Москвы, может рассматриваться как выборка из генеральной совокупности всех коммерческих банков этого округа, и как выборка из генеральной совокупности всех коммерческих банков Москвы, а также как выборка из коммерческих банков страны и т.д.
По виду различаются индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности, при групповом отборе — качественно однородные группы (серии) единиц, а комбинированный отбор предполагает сочетание первого и второго видов.
По методу отбора различают повторную и бесповторную выборку.
Бесповторным называется отбор, при котором попавшая в выборку единица не возвращается в исходную совокупность и в дальнейшем выборе не участвует; при этом численность единиц генеральной совокупности N сокращается в процессе отбора. При повторном отборе попавшая в выборку единица после регистрации возвращается в генеральную совокупность и таким образом сохраняет равную возможность наряду с другими единицами быть использованной в дальнейшей процедуре отбора; при этом численность единиц генеральной совокупности N остается неизменной (метод в социально-экономических исследованиях применяется редко). Однако, при большом N (N → ∞) формулы для бесповторного отбора приближаются к аналогичным для повторного отбора и практически чаще используются последние (N = const).
Репрезентативная выборка (representative sample) - одно из ключевых понятий анализа данных. Репрезентативная выборка - это выборка из генеральной совокупности с распределением F (x), представляющая основные особенности генеральной совокупности. Например, если в городе проживает 100 000 человек, половина из которых мужчины и половина женщины, то выборка 1000 человек из которых 10 мужчин и 990 женщин, конечно, не будет репрезентативной. Построенный на ее основе опрос общественного мнения, конечно, будет содержать смещение оценок и приводит к фальсификации результатов.
|
|
|
Необходимым условием построения репрезентативной выборки является равная вероятность включения в нее каждого элемента генеральной совокупности.
Выборочная (эмпирическая) функция распределения  дает при большом объеме выборки достаточно хорошее представление о функции распределения F (x) исходной генеральной совокупности.
дает при большом объеме выборки достаточно хорошее представление о функции распределения F (x) исходной генеральной совокупности.
Репрезентативная выборка – это такая выборка, в которой все основные признаки генеральной совокупности, из которой извлечена данная выборка, представлены приблизительно в той же пропорции или с той же частотой, с которой данный признак выступает в этой генеральной совокупности.
112. Варианты, частоты и относительные частоты. Дискретный вариационный ряд. Обычно полученные наблюдаемые данные представляют собой множество расположенных в беспорядке чисел. Просматривая это множество чисел, трудно выявить какую-либо закономерность их варьирования (изменения). Для изучения закономерностей варьирования значений случайной величины опытные данные подвергают обработке. Рассмотрим пример. На телефонной станции проводились наблюдения над числом Х неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты: 3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1;4; 3; 3; 1; 4; 2; 2; 1; 1; 2; 1; 0; 3; 4; 1; 3; 2; 7; 2; 0; 0; 1; 3; 3; 1; 2; 4;2; 0; 2; 3; 1; 2; 5; 1; 1; 0; 1; 1; 2; 2; 1; 1; 5. Здесь число X является дискретной случайной величиной, а полученные о ней сведения представляют собой статистические (наблюдаемые) данные. Операция, заключающаяся в том, что результаты наблюдений над случайной величиной, т. е. наблюдаемые значения случайной величины, располагают в порядке неубывания, называется ранжированием опытных данных. После проведения операции ранжирования опытные данные группируют так, что в каждой отдельной группе значения случайной величины будут одинаковы. Расположив приведенные выше данные в порядке неубывания и сгруппировав их, получают ранжированный ряд данных наблюдения
|
|
|
Из ряда чисел видно, что все 60 значений случайной величины разбиты на семь групп, в пределах каждой из которых все значения случайной величины одинаковы. Таким образом, имеется семь различных значений случайной величины: 0; 1; 2; 3; 4; 5; 7. Каждое такое значение обычно называют вариантом.
Значение случайной величины, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называется вариантом, а изменение этого значения варьированием.
Варианты будем обозначать малыми буквами конца латинского алфавита с соответствующими порядковому номеру группы индексами.
Для каждой группы сгруппированного ряда данных можно подсчитать их численность, т.е. определить число, которое показывает, сколько раз встречается соответствующий вариант вряде наблюдений. Такие числа называют частотой варианта.
Численность отдельной группы сгруппированного ряда наблюдаемых данных называется частотой или весом соответствующего варианта и обозначается тi, где i — индекс варианта.
В ряде случаев представляет практический интерес относительная частота того или иного варианта, называемая частостью.
Отношение частоты данного варианта к общей сумме частот всех вариантов называется частостью или долей этого варианта и обозначается рi, где i—индекс варианта, т.е.

Нетрудно заметить, что частость является статистической вероятностью появления варианта. Естественно считать частость выборочным аналогом (вычисленной по выборочным данным) вероятности рi появления значения хi, случайной величины X. Подсчитав частоты и частости для каждого варианта, наблюдаемые данные представляют в виде таблицы, которую называют дискретным вариационным рядом. В первой строке расположены- варианты, во второй- соответствующие частоты, в третьей- соответствующие частости.
|
|
|
Дискретным вариационным рядом распределения называется ранжированная совокупность вариантов хi с соответствующими им частотами или частностями.
Для рассмотренного примера ряд имеет вид:
| xi | |||||||
| mi | |||||||
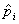
| 8/60 | 17/60 | 16/60 | 10/60 | 6/60 | 2/60 | 1/60 |
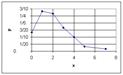
По данным дискретного вариационного ряда строят
полигон частот или относительных частот: ломаную, отрезки которой соединяют точки
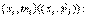
113. Частота и относительная частота, соответствующие заданному интервалу. Интервальный вариационный ряд.
Если изучаемая случайная величина является непрерывной, то ранжирование и группировка наблюдаемых значений зачастую не позволяют выделить характерные черты варьирования ее значений. Это объясняется тем, что отдельные значения случайной величины могут как угодно мало отличаться друг от друга и поэтому в совокупности наблюдаемых данных одинаковые значения величины могут встречаться редко, а частоты вариантов мало отличаются друг от друга.
Нецелесообразно также построение дискретного ряда для дискретной случайной величины, число возможных значений которой велико. В подобных случаях следует построить интервальный (вариационный) ряд распределения. Для построения такого ряда весь интервал варьирования наблюдаемых значений случайной величины разбивают на ряд частичных интервалов и подсчитывают частоту попадания значений величины в каждый частичный интервал.
Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами или частостями попаданий в каждый из них значений величины.
114. Гистограмма и полигон.
Каждую пару значений (xi, ni) из распределения выборки можно трактовать как точку на координатной плоскости. Точно так же можно рассматривать и пары значений (хi, Wi) относительного распределения выборки. Ломаная, отрезки которой соединяют точки (xi, ni), называется полигоном частот. Ломаная, соединяющая на координатной плоскости точки (xi, Wi), называется полигоном относительных частот. На рис. 18.9 показан полигон относительных частот для распределения, приведенного в примере 2.
|
|
|

Для случая непрерывного признака Х удобно разбить интервал (x min, x max) его наблюдаемых значений на несколько частичных интервалов длиной h каждый и найти для каждого из этих интервалов сумму частот nj, попавших в него. Ступенчатая фигура, состоящая из прямоугольников с основаниями длиной h и высотами nj/h (плотность частоты), называется гистограммой частот. Геометрический смысл гистограммы: нетрудно видеть, что площадь ее равна сумме всех частот или объему выборки. На рис. 18.10 изображена гистограмма объема n = 100.
Аналогичным образом определяется и гистограмма относительных частот: в этом случае высоты прямоугольников, составляющих ступенчатую фигуру, определяются отношениями сумм относительных частот, попадающих в интервал (x min + (j — 1) h, x min + jh), к длине интервала h, т.е. величинами Wj/h. Нетрудно видеть, что площадь гистограммы относительных частот равна единице (сумме относительных частот выборки).

115. Накопленные относительные частоты. Эмпирическая функция распределения. Кумулята. Графическое изображение зависимости между величинами дает возможность представить эту зависимость наглядно. Графики могут служить основой для открытия новых свойств, соотношений и закономерностей. Наиболее употребительными графиками для изображения вариационных рядов, т. е. соотношений между значениями признака и соответствующими частотами или относительными частотами, являются полигон, гистограмма и кумулята Полигон чаще всего используют для изображения дискретных рядов. Для построения полигона в прямоугольной системе координат на оси абсцисс в произвольно выбранном масштабе откладывают значения аргумента, т. е. варианты, а на оси ординат также в произвольно выбранном масштабе - значения частот или относительных частот. Масштаб выбирают такой, чтобы была обеспечена необходимая наглядность, и чтобы рисунок имел желательный размер. Далее в этой системе координат строят точки, координатами которых являются пары соответствующих чисел из вариационного ряда. Полученные точки последовательно соединяют отрезками прямой. Крайнюю "левую" точку соединяют с точкой оси абсцисс, абсцисса которой находится слева от рассматриваемой точки на таком же расстоянии, как абсцисса ближайшей справа точки. Аналогично крайнюю "правую" точку также соединяют с точкой оси абсцисс. Кумулята служит для графического изображения кумулятивного вариационного ряда. Для ее построения на оси абсцисс откладывают значения аргумента, а на оси ординат - накопленные частоты или накопленные относительные частоты. Масштаб на каждой оси выбирают произвольно. Далее строят точки, абсциссы которых равны вариантам (в случае дискретных рядов) или верхним границам интервалов (в случае интервальных рядов), а ординаты - соответствующим частотам (накопленным частотам). Эти точки соединяют отрезками прямой. Полученная ломаная и является кумулятой. По данным таблицы составить кумулятивный вариационный ряд, для которого построить кумуляту.
| Количество баллов x | ||||||||||||
| Число учащихся n |
Решение.
Cоставим кумулятивный вариационный ряд (см. таблицу ниже), для которого построим кумуляту.
| Количество баллов | ||||||||||||
| Частота | ||||||||||||
| Накопленная частота n |

116. Числовые характеристики выборки (выборочная средняя, выборочная дисперсия, выборочное стандартное отклонение).
Значения количественного признака х 1, х 2,..., хk в выборке можно рассматривать как независимые случайные величины. В таком случае нахождение статистической оценки неизвестного параметра теоретического распределения означает отыскание функции от наблюдаемых случайных величин, которая и даст нам приближенное значение искомого параметра. Укажем виды статистических оценок.
Несмещенной называется статистическая оценка  , математическое ожидание которой равно оцениваемому параметру
, математическое ожидание которой равно оцениваемому параметру 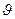 при любой выборке:
при любой выборке:

Смещенной называется оценка, при которой условие (18.51) не выполнено. Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки п. Состоятельной называется статистическая оценка типа (18.50), которая при п > 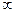 стремится по вероятности к оцениваемому параметру.
стремится по вероятности к оцениваемому параметру.
Теперь укажем виды числовых характеристик оценок. Прежде всего, это средние. Генеральная средняя для изучаемого количественного признака Х по генеральной совокупности
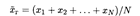
и выборочная средняя
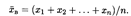
Если значения признака х 1, x 2, …, хk в выборке имеют соответственно частоты n 1, n 2,..., nk, то последнюю формулу можно переписать в виде

Можно показать, что выборочная средняя (18.52) является несмещенной оценкой; это аналог математического ожидания случайной величины.
117. Точечные статистические оценки неизвестных параметров теоретического распределения. Несмещенные, эффективные и состоятельные точечные оценки.
Задача оценивания параметров распределения генеральной – одна из основных задач математической статистики. На содержательном уровне задача оценивания параметров распределения формулируется так: располагая выборкой реализаций случайной величины Х, необходимо получить оценку  неизвестного параметра генеральной совокупности а и ее статистические свойства.
неизвестного параметра генеральной совокупности а и ее статистические свойства.
Оценивание параметров распределения осуществляется в два этапа. На первом этапе, на основании выборки х1, х2,...,, хn,строится статистика
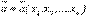 ,
,
значение которой при данной выборке х1, х2,...,, хn принимают за приближенное значение оцениваемого параметра а:
а 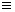
 .
.
Так как параметр генеральной совокупности оценивается числом, которое на числовой оси изображается точкой, то оценку 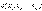 называют точечной.
называют точечной.
Для получения точечной оценки существует много статистик, которые могут быть использованы в качестве оценок. Поэтому второй этап оценивания состоит в выборе наилучшей оценки, что требует введения критерия качества получаемых оценок. Задача усложняется тем, что ввиду малого объема выборки требуется статистический подход к качеству оценки
По опытным данным (выборке) путем построения гистограммы или с помощью других средств можно попытаться выбрать вероятностную модель (определить закон распределения генеральной совокупности). При этом выборочные данные позволяют уточнить детали вероятностной модели. Знание вероятностной модели дает возможность прогнозировать будущие события, что важно для принятия решений. В приложениях обычно задаются определенным типом закона распределения генеральной совокупности (плотностью распределения)
f = f (x; a1, a2,..., am)
и по данным случайной выборки х1, х2,..., хn оценивают неизвестные параметры a1, a2,..., am. Чаще всего параметрами являются генеральное среднее и дисперсия, а качестве оценки тогда используют выборочные характеристики: выборочное среднее и выборочную дисперсию.
Екстр.ф. z = f(x;y) знайдений за умовою, що j(x;y) = 0 наз. умовним, а рів. j(x;y) = 0 наз. рів. зв’язку. Для знаходження умовного екстра. Вводиться ф. Лагранжа 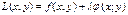 де
де  - множник Лагранжа.
- множник Лагранжа.
Умовний екстремум можна знайти 2 способами:
1)Якщо з рів. зв’язку легко знайти y=y(x) і потім підставити у ф. z = f(x;y), то задача знаходження умовного екстра. зводиться до відшукання екстра. ф. однієї змінної z = f(x;y(x))
2)Знайти координати екстр. точки враховуючи те, що вони повинні задовольняти трьом рів.: j(x;y) = 0; 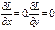
З цих рів. знайти  , визначити екстрем.
, визначити екстрем.
13. Задачі диференціювання та інтегрування. Означення первісної. Теорема про множину первісних.
Функція F(x) називається первісною для ф-ії f(x) на проміжку І, якщо на цьому проміжку F`(x)=f(x) або dF(x)=f(x)dx. Із означення виходить, що первісна F(x) – диференційована, а значить неперервна функція на проміжку І, і її вигляд суттєво залежить від проміжку, на якому вона розглядається. Теорема про множину первісних. Якщо F(x) – первісна для функції f(х) на проміжку І, то: 1) F(x)+С – також первісна для f(x) на проміжку І; 2)будь-яка первісна Ф(х) для f(x) може біти представлена у вигляді Ф(х)= F(x)+С на проміжку І. (Тут С=const називається довільною сталою).
Операція знаходження первісних для ф-ії f(x) називається інтегруванням f(x). Задача інтегрування функції на проміжку полягає в тому, щоб знайти всі первісні функції на цьому проміжку. Для розв’язання задачі інтегрування функції достатньо знайти одну будь-яку первісну на розглядуваному проміжку, наприклад F(x), тоді (за теоремою про множину первісних) F(x)+С – загальний вигляд всієї множини первісних на цьому проміжку. Означення: Ф-ія F(x)+С, зо являє собою загальний вигляд всієї множини первісних для ф-ії f(x) на проміжку І і позначається
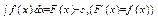
де f(x) – підінтегральна ф-ія; f(x)dx – підінтегральний вираз; dx – диференціал змінної інтегрування.
14.Невизначений інтеграл та його властивості.
Теорема Коші. Для існування невизначеного інтеграла для ф-ії f(x) на певному проміжку достатньо, щоб f(x) була неперервною на цьому проміжку.
Неінтегровні інтеграли – які неможливо записати через основні елементарні ф-ії.
Властивості, що випливають із означення невизн. інт:
1)Властивості, що випливають з означ.:
a) похідна від невизначеного інтеграла дорівнює підінтегральній ф-ії:
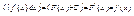
b) Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу.
c) 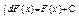
2)Властивості, що відображають основні правила інтегрування:
d) Сталий множник, що не дорівнює нулю, можна виносити з-під знака інтеграла.
i) Невизн. інтеграл від суми функцій дорівнює сумі невизначених інтегралів від цих функцій, якщо
15.Інтегрування невизначеного інтеграла заміною змінної
Мета методу заміни зменної перетворити даний інтеграл до такого вигляду, який простіше інтегрувати.
Теорема: Якщо f(x) неперервна, а 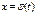 має неперервну похідну, то інтеграл
має неперервну похідну, то інтеграл
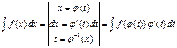
Наслідок:
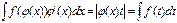
16.Інтегрування невизначеного інтегралу частинами
Теорема: Якщо функції u(x) та v(x) мають неперервні похідні, то: 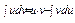
На практиці ф-ії u(x) та v(x) рекомендується вибирати за таким правилом: при інтегруванні частинами підінтегральний вираз f(x)dx розбивають на два множники типу udv, тобто f(x)dx=udv; при цьому ф-ія u(x) вибирається такою, щоб при диференціюванні вона спрощувалася, а за dv приймають залишок підінтегрального виразу, який мітить dx, інтеграл від якого відомий, або може бути просто знайдений.
Деякі типи інтегралів і їх заміни:


де Р(х) – многочлен, Q(x) – алгебраїчна ф-ія.
17.Інтегрування найпростіших раціональних функцій
Відношення двох многочленів 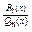 називається раціональним дробом. Раціональний дріб правильний, якщо степінь многочлена в чисельнику менший степеня многочлена в знаменнику, тобто n<m. Якщо ж n³m, то дріб неправильний. Найпростіші раціональні дроби (4 типи): 1.
називається раціональним дробом. Раціональний дріб правильний, якщо степінь многочлена в чисельнику менший степеня многочлена в знаменнику, тобто n<m. Якщо ж n³m, то дріб неправильний. Найпростіші раціональні дроби (4 типи): 1.  2.
2. 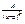 3.
3.  4.
4. 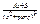 де k³2, kÎN, D=p2-4q<0
де k³2, kÎN, D=p2-4q<0
Теорема: Будь-який правильний раціональний нескоротний дріб можна представити у вигляді скінченого числа найпростіших дробів використовуючи такі правила:
1) Якщо Qm(x)=(x-a)k×gm-k(x), то:
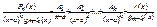
2) Якщо Qm(x)=(x2+px+q)k×gm-2k(x), то:

де Аі, Ві, 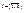 – деякі коефіцієнти,
– деякі коефіцієнти,  та
та  правильні раціональні дроби.
правильні раціональні дроби.
Методика інтегрування раціональних ф-ій: 1. Якщо підінтегральна ф-ія – неправильний раціональний дріб, то за допомогою ділення його розкладають на суму многочлена і правильного раціонального дробу. 2. Знаменник правильного раціон. дробу розкладають на множники. По вигляду знаменника, правильний раціон. дріб представляють у вигляді найпростіших дробів, використовуючи метод невизначених коефіцієнтів. 3. Інтегрують цілу частину і найпростіші дроби.
18. Інтегрування деяких ірраціональних функцій.
1) 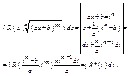
2) 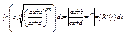
3) 
Підінтегральна ф-ія  після виділення повного квадрата і заміни
після виділення повного квадрата і заміни 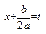 раціоналізується тригонометричними підстановками.
раціоналізується тригонометричними підстановками.
19.Інтегрування довільної раціональної функції
Означення: Відношення двох многочленів 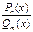 називається раціональним дробом.
називається раціональним дробом.
Означення: Раціональний дріб правильний, якщо степінь многочлена в чисельнику менший степеня многочлена в знаменнику, тобто n<m. Якщо ж n³m, то дріб неправильний.
Найпростіші раціональні дроби (4 типи):
1. 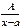 2.
2.  3.
3. 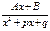 4.
4. 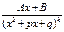
де k³2, kÎN, D=p2-4q<0
Теорема: Будь-який правильний раціональний нескоротний дріб можна представити у вигляді скінченого числа найпростіших дробів використовуючи такі правила:
1) Якщо Qm(x)=(x-a)k×gm-k(x), то:


2) Якщо Qm(x)=(x2+px+q)k×gm-2k(x), то:

де Аі, Ві, 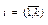 – деякі коефіцієнти,
– деякі коефіцієнти,  та
та  правильні раціональні дроби.
правильні раціональні дроби.
20.Інтегрування тригонометричних функцій
Розглянемо ò R(sin x,cos x)dx, де R – раціональна ф-ія відносно sin, cos, тобто над sin, cos викон. лише арифметичні дії та піднесення до цілого степеня. Існують такі підстановки, що за їх допомогою інтеграл ò R(sinx,cosx)dx завжди може бути зведений до інтеграла від раціональної ф-ії ò R*(t)dt, загальна схема інтегрування якої розроблена.
1) Універсальна тригонометрична підстановка 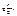 . На практиці універсальну тригонометричну підстановку використовують, якщо sin x, cos x входять в невисокому степені, інакше підрахунки будуть складні.
. На практиці універсальну тригонометричну підстановку використовують, якщо sin x, cos x входять в невисокому степені, інакше підрахунки будуть складні.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 421; Нарушение авторских прав?; Мы поможем в написании вашей работы!