Теория пределов, второй замечательный предел

Тема: Теория пределов, второй замечательный предел

29 (первого уровня сложности). Лодка массой m двигалась в воде с по­стоянной скоростью v . В некоторый момент времени двигатель вы­ключается. Найти закон дальнейшего изменения скорости со време­нем, считая силу сопротивления пропорциональной скорости (коэффициент пропорциональности к).

Раздел 2. Введение в анализ

30.Задача о непрерывном начислении процентов (второго уровня сложности). Первоначальный вклад в банк составил S(0) = 1000 усл. единиц. Найти наращенное за 10 лет значение суммы, если оно реинвестиру­ется по постоянной ставке i = 25 % при следующих значениях m: а) 1 раз в год; б) ежеквартально; в) непрерывно.

Решение: a) S(t) = S (l + p/100) 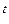, р = 25, t = 10

б) S(t) = S (l + р/100n) 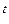, n = 4, р = 25, t =10;

в) S(t) = 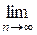(S (1 + p/100n) ) = S e .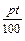

31 (второго уровня сложности). Найти коэффициент наращения А (г; при ре­инвестировании по постоянной ставке i = 1, при t = 1 год, еже­годно, ежеквартально, ежемесячно, ежечасно, ежеминутно и непре­рывно. Вычислить i , для каждого из случаев.

32 (второго уровня сложности). Количество возможных клиентов некото­рой фирмы, в результате хорошо организованной рекламы, увеличи­вается со временем пропорционально количеству знающих о услугах этой фирмы в данный момент. Найти закон изменения количества клиентов, если М0)= А , с - коэффициент пропорциональности. Как изменится количество клиентов через два дня, если за первый день количество возможных клиентов возросло на 25%.

Приведем два примера сравнения бесконечно малых и бесконечно больших, сравнение которых аналогично.

33. Почему вода, распыляемая форсункой, резко снижает свою температуру?

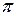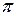Капля воды, испаряясь, уменьшает свой объем V = R и площадь поверхности = 4 R ,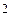

где R — ее радиус.

При R 0 V и становятся бесконечно малыми.

Сравним их: .

Этот результат дает возможность понять, почему вода, распыляемая форсункой, резко снижает свою температуру. Дело в том, что при раздроблении большой капли на маленькие суммарный объем остается тем же, а суммарная площадь поверхности резко возрастает. На ее образование необходимо затратить энергию, которая покрывается за счет кинетической энергии молекул воды, что и приводит к снижению температуры.

34. Рассмотрим модель однородной Вселенной с равномерно распределённой плотностью материи. Суммарная масса М Вселенной радиуса R равна

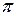
М = R .

Она притягивает частицу массы m с силой F

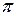
F = mR,

где - гравитационная постоянная. Если Вселенная бесконечна, то

R 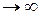и F 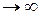— это так называемый гравитационный парадокс Вселенной.

Как же устранить этот парадокс? Самым простым решением являет­ся конечность Вселенной (R=const), но тогда ее ожидает «тепловая смерть» в соответствии со вторым началом термодинамики. Эта неприятность отсутствует в бесконечной Вселенной, поскольку энергия и энтропия здесь бесконечны и говорить об их возрастании или убывании.

Пусть поэтому R 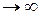, но 0, так что pR= const. В этом случае гравитационный парадокс снимается, но гипотезу 0 не подтверждают непосредственные наблюдения. Удовлетворительное решение этого парадокса получается в рамках теории «большого взрыва», согласно которой около 15 — 20 млрд лет назад наша Вселенная выплеснулась из бесконечно (в смысле пространства—времени) частицы и с тех пор расширяется со скоростью, пропорциональной расстоянию до рассматриваемого объекта (закон Хаббла).

На определённом расстоянии скорость объекта становится равной скорости света, а более удаленные объекты проваливаются за «горизонт событий» и от них к нам не приходит ни свет, ни тяготение. Поскольку объём пространства внутри «горизонта событий» конечен, то гравитационный парадокс снимается.

35. Приведем пример применения понятия предела функции в экономических расчетах. Рассмотрим обыкновенную финансовую сделку: предоставление в долг суммы S с условием, что через период времени Т будет возвращена сумма S . Определим величину r относительного роста формулой

r = (1)

Относительный рост можно выразить в процентах, умножив полученное значение r на 100.

Из формулы (1) легко определить величину S : S =S (l +r)

При расчете по долгосрочным кредитам, охватывающим несколько полных лет, используют схему сложных процентов. Она состоит в том, что если за 1-й год сумма S возрастает в (1 + r) раз, то за второй год в (1 + r) раз возрастает сумма 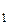S = S (l + r), то есть S = S (1 + r) 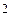. Аналогично получается S 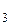= S (1 + г) . Из приведенных примеров можно вывести общую формулу для вычисления роста суммы за n лет при расчете по схеме сложных процентов:

S = S (1 + r) .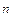

В финансовых расчетах применяются схемы, где начисление сложных процентов производится несколько раз в году. При этом оговариваются годовая ставка r и количество начислений за год k. Как правило, начисления производятся через равные промежутки времени, то есть длина каждого промежутка Т 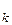составляет часть года.

Тогда для срока в Т лет (здесь Т не обязательно является целым числом) сумма S рассчитывается по формуле

S = S (1 + ) . (2)

Здесь m = 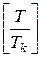— целая часть числа , которое совпадает с самим числом, если, например, Т- целое число.

Пусть годовая ставка равна r и производится n начислений в год через равные промежутки времени. Тогда за год сумма S наращивается до величины, определяемой формулой

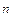S = S (1 + ) . (3)

В теоретическом анализе и в практике финансовой деятельности часто встречается понятие "непрерывно начисляемый процент". Чтобы перейти к непрерывно начисляемому проценту, нужно в формулах (2) и (3) неограниченно увеличивать соответственно, числа к и n (то есть устремить к и n к бесконечности) и вычислить, к какому пределу будут стремиться функции S и S . Применим эту процедуру к формуле (3):

S =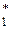

Заметим, что предел в фигурных скобках совпадает со вторым замечательным пределом. Отсюда следует, что при годовой ставке r при непрерывно начисляемом проценте сумма S за 1 год наращивается до величины S 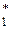, которая определяется из формулы

S 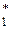= S e (4)

Пусть теперь сумма S предоставляется в долг с начислением процента n раз в год через равные промежутки времени. Обозначим r годовую ставку, при которой в конце года сумма S наращивается до величины S 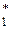из формулы (4). В этом случае будем говорить, что r — это годовая ставка при начислении процента n раз в год, эквивалентная годовому проценту r при непрерывном начислении. Из формулы (3) получаем

S 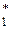= S (1 + ) .

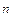Приравнивая правые части последней формулы и формулы (4), полагая в последней T = 1, можно вывести соотношения между величинами r и r :

r = n (1 + ), r = n .

Эти формулы широко используются в финансовых расчётах.

36. Бревна и дрова на складах лесоматериалов укладывают в штабеля (штабель с дровами обычно называют поленницей) различной формы (рис.) Учет уложенных в штабеля лесоматериалов ведётся с помощью коэффициента полнодревесности штабеля, под которым понимается отношение объема древесины в штабеле к геометрическому объёму штабеля (первый меньше из-за наличия пустот между стволами). Докажите, что значение коэффициента полнодревесности треугольного профиля, составленной из одинаковых цилиндрических чурок, не выходит из интервала (0,60; 0,91).

37. Левый и правый пределы

Примеры, когда левый и правый пределы функции не равны:

1) на графике теплоёмкости тела при нагревании последнего (переход из твердого состояния в жидкое, из жидкого в газ);

2) закон распределения неравномерной нагрузки вдоль длины балки;

3) величина скорости при ударе.

38. Приведем примеры разрывных функций.

1. Примером функции, имеющей много точек разрыва, является функция, отражающая ход выпол­нения плана продажи сельскохозяйственным пред­приятием молока за пятидневку при условии, что регистрация происходит ежедневно, f(x) — в литрах, х — в дн. Формула для описания подобной функции может быть следующей.

39. Зависимость возбуждения Е (например, нер­вных клеток мышц и т. д.) от времени при внешнем воздействии изображается разрывной функцией.

Если величину возбуждения выразить в каких-либо единицах, то график функции E(t) будет иметь вид, изображенный на рис. В момент t клетка получает сигнал. Возбуждение происходит в момент . За­мкнутый интервал [t , t ] называется латентным периодом. Возбуждение клетки в момент t = t происходит мгновенно до максимальной величины, затем оно постепенно уменьшает­ся до тех пор, пока не будет дан новый сигнал. Если сигнала нет достаточно долго, то E(t) становится равной нулю Зависимость изменения биомассы микроорганиз­мов, чувствительных к температурным колебани­ям,—разрывная функция температуры. При возра­стании температуры общая биомасса т увеличива­ется. Однако, когда температура очень высокая, вся колония погибает. Величина m скачкообразно меня­ясь, становится равной 0. Функция Хевисайда описывает мгновенное включение какого-либо воз­действия на объект или переход из одной среды в другую:

Дата добавления: 2015-06-04