Законы распределения функции двух случайных величин

Вероятностный смысл функции распределения двух СВ

Подобно тому, как закон распределения функции одного случайного аргумента Y = j(X) связан с вероятностью попадания аргумента в область D (y) = { x: j(x)< y }, функция распределения СВ Y = j(X ₁, X ₂) определяет вероятность попадания в соответствующую двумерную область:

F_y (y) º G (y) = P (Y<y) = P ((X ₁, X ₂) Î D (y) = { x ₁, x ₂ : j(x ₁, x ₂) < y }).

Если система (X ₁, X ₂) имеет совместную плотность f (x ₁, x ₂), функцию распределения можно получить интегрированием по области D (y):

Общий принцип получения законов распределения функций СВ сводится к целесообразному представлению области интегрирования.

Пример 1: распределение площади проекции вращающегося параллелепипеда

Рис. 10.1. Поверхность S (q, j) и ее линии уровня

Площадь проекции беспорядочно вращающегося параллелепипеда на плоский экран связана со сферическими углами q, j соотношением (9.6). Чтобы построить функцию распределения F_S (s) = P (S < s), нужно сформировать область возможных значений D (s) = {q, j: S (q, j) < s }, и интегрировать закон распределения f (q, j) = 1/ (2p) cos j по этой области. Построим поверхность S (j, q) для параллелепипеда 10´8´4 в диапазоне углов 0 < j < p/2, 0 < q < p/2 (рис. 10.1):

>> a=10;b=8;c=4;A=c*b;B=a*c;C=a*b;

>> [Fi, Teta]= meshgrid(0:0.1:pi/2,0:0.1:pi/2);

>> S=A*sin(Fi)+(B*sin(Teta)+C*cos(Teta)).*cos(Fi); surfc(Fi, Teta, S)

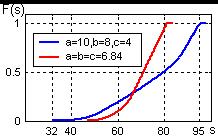
Рис. 10.2. Функция распределения F (s)

Из графика видно, что область интегрирования D (s) для вероятности G (s) = P (S < s) расположена между соответствующей линией уровня s и линией j = p/2. Файл-функция Para3_Distrib (Листинг 10.1, Приложение 10) выполняет численное интегрирование по области D (s) в соответствии с конфигурацией линий уровня. Построим функ­цию распределения F (s) (рис. 10.2), и в качестве простой проверки сеточной функции вычислим среднюю площадь, которая должна быть равной (A + B + C)/2 = 76:

>> [x,F, f]=Para3_Distrib(a,b,c);plot(x,F), hold on,m = Trap(x.*f,x),d=Trap(f.*(x-m).^2,x)

m = 75.9503 d = 223.5303

Алгоритмическое построение функции распределения позволяет исследовать вероятностную модель готовых поражающих элементов в форме параллелепипеда. Построим для сравнения функцию распределения проекции равновеликого куба:

>> h=(a*b*c)^(1/3);

[x,F,f]=Para3_Distrib(h,h,h); plot(x,F),m=Trap(x.*f,x),M=6*h^2/4, d = Trap(f.*(x-m).^2,x)

m = 70.2376 M = 70.1784 d = 50.8886

Первый начальный момент m практически совпал с точным значением M средней площади проекции согласно лемме Коши. Графики на рис. 10.2 показывают меньший разброс площади проекции компактного тела, что подтверждает и вычисленная дисперсия d. Оптимизация линейных размеров поражающего элемента может существенно повлиять на эффективность действия. Еще большее влияние может оказать изменение межреберных углов, но такой анализ не предусмотрен в программе Para3_Distrib, расчетные процедуры в которой построены для параллелепипедов.

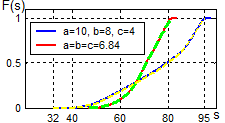
Рис. 10.3. Сравнение точных и статистических функций распределения F (s)

Объектный метод построения распределения площади проекции выпуклого многогранника

Программа Mid_S (Листинг 9.10) осуществляет статистическое моделирование случайных ориентаций экрана в пространстве, вычисляет площадь проекции многогранника, строит гистограмму и статистическую функцию распределения (с помощью SmartHist, Листинг 3.1). По умолчанию распределение принимается равно­мерным на сфере. Применим программу Mid_S к параллелепипеду a ´ b ´ c и равновеликому кубу из предыдущего примера, чтобы убедиться в точности статистического распределения:

>> [F,f]=Mid_S(ParaShape([a b c])); [F1,f1]=Mid_S(ParaShape([h h h])); Show (F,'y:',F1,'g:')

Статистические функции распределения выведены пунктирными линиями на графики, полученные ранее, и они практически совпали (рис. 9.10). Преимущество программы Mid_S в том, что ее можно использовать как электронную формулу для построения законов распределения случайной площади проекций произвольных многогранников.

Применение объектного метода к произвольному многограннику Рис. 10.4.

Построим закон распределения проекции случайно ориентированной косой ромбической призмы, используемой в качестве имитатора осколков [2, рис. 16.2]. Создать такой геометрический объект можно аффинным преобразованием параллелепипеда (рис. 10.4):

>> a=10;h=10;beta=45;ksi=45; R=ParaShape([a a h]);

>> A=Affinor(3,beta/2,221,beta,123,ksi); Fragm=R*A

Объект Fragm может вычислять свои характеристики. Например, объем, среднюю площадь миделя, массу, параметр формы фрагмента можно определить следующим образом:

>> V =Volume(Fragm), Sm=Area(Fragm)/4, m =V*0.0078, FI=Sm/V^(2/3)

V = 707.1068 Sm = 150.0000 m = 5.5154 FI = 1.8899

Рис. 10.5.

Он также обеспечивает необходимыми данными анализ проекций (площади граней, направления нормалей), благодаря чему функцию распределения площади проекции можно получить подстановкой объекта в электронную формулу Mid_S (рис. 10.5):

>> [F,f]=Mid_S(Fragm); plot(F.x,F.F,f.x,f.f/max(f.f))

Кривая плотности распределения нормирована модальным значением. Легко проверить выполнение основного свойства и МО, которое должно быть близким к 150:

>> Trap(f.f,f.x), Ms=Trap(f.x.*f.f,f.x)

ans = 1.0000 Ms = 150.0966

Моделирование произвольного многогранника Рис. 10.5.

Создадим объект класса Prism на основании, представленном объектом класса ParaGram со сторонами a=10 и острым углом beta=45°, а затем отсечем часть призмы плоскостью, наклоненной под углом ksi=45° к большой диагонали основания:

>> a=10; beta=45; ksi=45; h=10; PR=Prism(ParaGram([a a beta/180*pi]),50);

>> PL=Rot(Plane([0 0 1]),3,beta,2,ksi);T=sect(PR,move(PL,[0;0;25]));

Метод Prism/sect возвращает два многогранника – верхний T{1} и нижний T{2}. Готовый фрагмент получим отсечением нижней части объекта T{1} смещенной на h вверх плоскостью PL (рис. 10.5):

>>T1=sect(T{1},move(PL,[0;0;25+h]));Frag=T1{2};Show(T1{1},303,20,T{2},Frag,303,10)

Объект Frag имеет ту же форму и размеры, что и результат аффинного преобразования Fragm, но он получен более универсальным способом, которым можно образовать любой многогранник.

Пример 4: Перекрытие прямоугольных областей

На прямоугольник с размерами L_x ´ L_z (цель) брошен меньший прямоугольник l_x ´ l_z, центр которого распределен по нормальному закону с параметрами m_x, s _x, m_z, s _z, r = 0 в системе координат, связанной с центром большого прямоугольника.

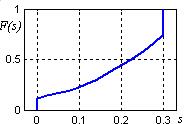
Рис. 10.7. Функция распределения площади перекрытия

Случайная величина U – относительная пло­щадь перекрытия прямоугольников, т.е. отношение площади перекрытия к площади цели. Закон распределения U (рис. 10.7) построен методом статистических испытаний с помощью класса «умных» прямоугольников так же, как в Лекции 3, где этот метод использован с равномерным распределением прямоугольников.

>> A=Rect(200,100); B=Rect(100,60);N=1000;X=Norm_2([40,50]);Z=Gen(X,N);

>> for i=1:N S(i)=Area(Sect(A,MOve(B,Z(:,i)))); end, [F,f]=SmartHist(S);Show(F)

Дата добавления: 2015-06-25