Лешек Рутковский

Председатель Польского общества нейронных сетей

Введение

ГЛАВА1 ВВЕДЕНИЕ

В последние годы большой интерес вызывает проблематика ней­ронных сетей, генетических алгоритмов и нечетких систем. Эти направле­ния относятся к научной области, определяемой в англоязычной литера­туре термином Computational Intelligence. Взаимосвязи между нейронны­ми сетями, генетическими алгоритмами и нечеткими системами послужи­ли причиной того, что IEEE (Institute of Electrical and Electronics Engineers - США) создал Всемирный Конгресс Computational Intelligence [10]. В рам­ках этого конгресса в период с 26 июня по 2 июля 1994 г. в Орландо, штат Флорида (США) были проведены три конференции:

а) IEEE International Conference on Neural Networks,

б) IEEE International Conference on Fuzzy Systems,

в) IEEE International Conference on Evolutionary Computation.

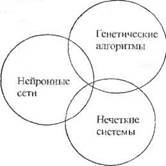
В 1995 - 1997 гг. каждая из этих конференций проводилась неза­висимо, но в 1998 г. вновь был организован Конгресс, проведенный на этот раз в Анкоридже на Аляске (США). На рис. 1.1. видно, что задачи нейронных сетей, генетических алгоритмов и нечетких систем могут рассматриваться вне связи между собой, однако их взаимозависимость оказывается необычайно важной. В частности, генетические алгорит­мы можно применять для подбора весов и топологии нейронной се­ти, а также для формирования базы правил и функций принадлежности

нечеткой системы.

ВЫЧИСЛИТЕЛЬНЫЕ

В свою очередь, нейронные сети позволяют выбирать соответ­ствующие параметры для самих генетических алгоритмов (параме­тры скрещивания и мутации); саму философию нейронных сетей можно заложить в фундамент не­четких систем, которые в результа­те обретают способность к обуче­нию.

ТЕХНОЛОГИИ Рис. 1.1. Взаимосвязи между нейрон­ными сетями, генетическими алгорит­мами и нечеткими системами.

Кроме того, методы теории нечетких множеств позволяют подбирать как упомянутые выше параметры генетических алгорит­мов, так и коэффициенты, опреде­ляющие скорость обучения ней­ронных сетей.

В Польше перечисленные выше проблемы интенсивно ис­следуются во многих научных центрах. В области нейронных се­тей первым достаточно полным

и очень полезным изданием считается книга профессора Р. Тадеусе-вича [7]. В настоящее время некоторые фрагменты этой книги представ­ляются автором также и на видеокассете [8]. В последующие годы увиде­ли свет и другие издания: книга, подводящая итоги работы коллектива под руководством профессора Ю. Корбича [3], монография профес­сора С. Осовского [5] и работа, представляющая результаты исследова­ний группы профессора Т. Каспшака в области клеточных нейронных се­тей [2].

Следует также отметить факт, что некоторые монографии поль­ских авторов известны и по достоинству оценены в мировой литературе. В частности, можно назвать:

а) по нейронным сетям - книги профессора Я. Журады [9] и про­
фессора А. Чихотского (с соавтором) [1];

б) по нечетким системам - книга профессора В. Педрыша [6];

в) по генетическим алгоритмам - книга профессора 3. Михалеви-
ча [4].

Поскольку ни одно из упомянутых прекрасных изданий не охваты­вает одновременно все три ветви, объединяемые под названием «вычислительные технологии», авторы настоящей работы поставили пе­ред собой задачу раскрыть перед читателем необычайно интересные возможности нейронных сетей, генетических алгоритмов и нечетких сис­тем, а также их композиций.

В главе 2 представлены основные структуры одно и многослойных нейронных сетей и алгоритмы их обучения. В первой части описывается перцептрон и системы типа Адалайн. Далее приводятся два алгоритма обучения многослойных нейронных сетей: классический и наиболее час­то применяемый алгоритм обратного распространения ошибки, а также значительно более быстрый алгоритм, основанный на рекуррентном ме­тоде наименьших квадратов.

В главе 3 обсуждаются системы, использующие нечеткую логику. Они особенно полезны в ситуации, когда доступные знания представле­ны в виде правил, основанных на нечетких множествах и лингвистичес­ких переменных. Системы этого типа де-факто признаны стандартом в Японии, где они применяются в автоматических стиральных и посудо­моечных машинах, видеокамерах и фотоаппаратах, кондиционерах и ав­томобилях. Излагаются элементы теории нечетких множеств и нечеткого вывода, также описывается функционирование различных нечетких про­цессоров.

Основам реализации генетических алгоритмов посвящена глава 4. Как известно, естественный путь развития мозга - это эволюционный процесс, с которым связаны специфические методы проб и ошибок. Идеи эволюционных изменений привели к созданию генетических алгоритмов, применяемых для обучения нейронных сетей и в системах, использую­щих нечеткую логику.

В книге представляются не только раздельные описания нейрон­ных сетей и нечетких систем, но и (в главе 5) новейшие результаты, полу­чаемые при их объединении. Композиции этого типа сохраняют и усили­вают достоинства как нейронных сетей, так и нечетких систем. Они потен-

Список литературы

Глава 1. Введение

циально применимы во всех ситуациях, когда конструктор системы рас­полагает и количественной (численные данные), и качественной (лингви­стические правила) информацией.

В конце каждой главы приводится список литературы.

Вопросы, обсуждаемые в книге, подробно иллюстрируются имита­ционными примерами, реализованными с помощью следующих пакетов программ:

1. FLiNN (программа написана на кафедре Компьютерной инженерии
Политехнического университета г. Ченстохова (Польша));

2. FlexTool (GA) M2.1 (Flexible Intelligence Group) - пакет, взаимодей­
ствующий с комплексом MATLAB (The MathWorks Inc.);

3. Evolver (Axcelis, Inc.) - пакет, взаимодействующий с программой
Excel (Microsoft Corp.);

4. BrainMaker и Genetic Training Option (California Scientific Software);

5. Fide (Aptronix, Inc.);

6. Fuzzy Logic Toolbox - прикладной пакет программ комплекса MAT-
LAB (The MathWorks, Inc.).

Выражаем признательность господам Уве фон Аммон и Марку Скарбек-Козетульскому из фирмы Motorola, благодаря любезности кото­рых мы получили пакет Fide.

Первый опыт работы с перечисленными программными средства­ми мы приобретали совместно со студентами четвертого курса Политех­нического университета г. Ченстохова по специальности «Электроника и компьютерная инженерия», которых хотелось бы поблагодарить за со­трудничество в ходе учебных занятий. Мы также сердечно благодарим госпожу Ренату Марчиняк и магистра инженера Артура Стажевского за труд по подготовке рисунков и рукописи.

Особую признательность выражаем рецензентам - профессору Юзефу Корбишу и профессору Рышарду Тадеусевичу за внимательное ознакомление с рукописью и очень полезные замечания.

Список литературы

[1] Cichocki A, Unbehauen R., Neural Networks for Optimization and

Signal Processing, Wiley, Chichester 1993. [2] Kacprzak Т., Slot K., Sieci neuronowe komorkowe. Teoria, projek-

towanie, zastosowania, PWN, Warszawa-Lodz 1994. [3] Korbicz J., Obuchowicz A., Ucinski D., Sztuczne sieci neuronowe,

podstawy i zastosowania, Akademicka Oficyna Wydawnicza,

Warszawa 1994. [4] Michalewicz Z, Genetic Algorithms + Data Structures = Evolution

Programs, Springer-Verlag, Berlin 1994. [5] Osowski S., Sieci neuronowe w ujeciu algorytmicznym, WNT,

Warszawa 1996. [6] Pedrycz W., Fuzzy Control and Fuzzy Systems, Wiley, New York

1993. [7] Tadeusiewicz R., Sieci neuronowe, Akademicka Oficyna

Wydawnicza, Warszawa 1993.

[8]

[9]

Tadeusiewicz R., Wprowadzenie do sieci neuronowych, kaseta wideo, Polskie Towarzystwo Sieci Neuronowych, Czestochowa 1996. Zurada J. M., Introduction to Artificial Neural Systems, West Publishing Company, Boston 1992. [10] Zurada J. M., Marks R. J., Robinson C. J., (red.), Computational Intelligence: Imitating Life, IEEE Press, New York 1994.

2.2. Нейрон и его модели

ГЛАВА2

МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ

2.1. Введение

Нейронные сети можно рассматривать как современные вычисли­тельные системы, которые преобразуют информацию по образу процес­сов, происходящих в мозгу человека. Обрабатываемая информация име­ет численный характер, что позволяет использовать нейронную сеть, на­пример, в качестве модели объекта с совершенно неизвестными харак­теристиками. Другие типовые приложения нейронных сетей охватывают задачи распознавания, классификации, анализа и сжатия образов.

Проблематика нейронных сетей в девяностых годах XX века на­шла отражение в сотнях монографий, среди которых можно упомянуть изданные в Польше работы [10, 11, 13, 17, 24]¹ и некоторые заграничные публикации [3, 5, 7, 8, 15, 21, 28]. Также следует упомянуть о прекрасных обзорных статьях, которые стали катализатором дальнейших исследова­ний как в Польше (Р. Тадеушевич [22]), так и за границей (Р. Липпманн [14]).

Свыше 80 % всех приложений нейронных сетей относится к так на­зываемым многослойным сетям без обратных связей. В них сигнал пере­сылается в направлении от входного слоя через скрытые слои (если они имеются) к выходному слою. Сети именно такого типа будут рассматри­ваться в последующих главах книги в контексте генетических алгоритмов и нечетких систем. Поэтому в настоящей главе мы обсудим в первую оче­редь базовые элементы многослойных нейронных сетей - персептрон и системы типа Адалайн (с линейным и нелинейным выходом), после че­го определим два алгоритма обучения этих сетей: алгоритм обратного распространения ошибки и рекуррентный алгоритм метода наименьших квадратов.

Хотелось бы подчеркнуть, что в нашей монографии представляет­ся достаточно узкий, однако весьма важный с прикладной точки зрения фрагмент необычайно обширной области знаний, которая получила на­звание «искусственные нейронные сети». Приглашаем читателя к более углубленному изучению литературных источников, перечень которых приводится в конце главы.

2.2. Нейрон и его модели

Базовый элемент нервной системы (см. [23]) - это нервная клетка, называемая нейроном. В нейроне можно выделить тело клетки, называ­емое сомой, а также исходящие из него два вида отростков: а) по кото­рым в нейрон поступает информация - дендриты и б) по которому ней-

рон передает информацию - аксон. Каждый нейрон имеет только один выходной отросток, по которому он может передавать импульс несколь­ким другим нейронам.

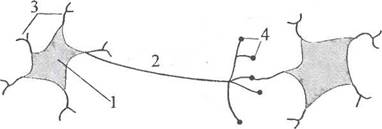
Одиночный нейрон принимает возбуждения от огромного количе­ства нейронов (их число может достигать тысячи). Считается, что мозг че­ловека состоит из порядка 10¹¹ нейронов, которые имеют между собой примерно 10¹⁵ соединений. Каждый нейрон передает возбуждение дру­гим нейронам через нервные стыки, называемые синапсами, при этом процесс передачи сигналов имеет сложную электрохимическую природу. Синапсы играют роль репитеров информации, в результате функциони­рования которых возбуждение может усиливаться или ослабляться. Как следствие, к нейрону приходят сигналы, одна часть из которых оказыва­ет возбуждающее, а вторая - тормозящее воздействие. Нейрон суммиру­ет возбуждающие и тормозящие импульсы. Если их алгебраическая сум­ма превышает некоторое пороговое значение, то сигнал с выхода нейро­на пересылается посредством аксона к другим нейронам. На рис. 2.1. представлена упрощенная модель нейрона.

Рассмотрим модель нейрона, связанную с первыми попытками формализовать описание функционирования нервной клетки. Введем следующие обозначения:

и_ь.... u_N- входные сигналы данного нейрона, приходящие от дру­гих нейронов;

w_b..., w_N - синаптические веса;

у- выходной сигнал нейрона;

v - пороговое значение.

Формула, описывающая функционирование нейрона, имеет вид

N 1 При У WjU; > V,

У-

(2.1)

0 При

Переработанная версия монографии проф. С. Осовского [17] под назва­нием «Нейронные сети для обработки информации» издана в 2002 г. на русском языке издательством «Финансы и статистика». - Прим. перев.

Рис. 2.1. Упрощенная модель нейрона и его соединения с соседним нейроном: 1 - тело клетки, 2 - аксон, 3 - дендриты, 4 - синапсы.

Глава 2. Многослойные нейронные сети и алгоритмы их обучения

2.2. Нейрон и его модели

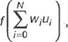
Модель (2.1) может быть представлена в виде

(2.2)

где

w =

(2.3)

1 при х>0 О при х<0

а также w_o = v,u_o=1.

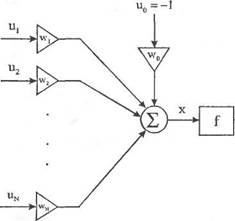
Формула (2.2) описывает модель нейрона, представленную на рис. 2.2. Эта модель была предложена в 1943 г. МакКаллоком и Питт-сом [16]. В качестве функции Сможет приниматься не только единич­ная функция (2.3), но и другие пороговые функции вида

(2.4)

1 при х>0, f(x) - | _ ₁ при х < О.

или

(2.5)

1 при х> 1, f(x) = -j -1 при х < -1, х при |х|<1.

На начальной фазе моделирования биологических нейронных сетей применялись пороговые функции (2.3), (2.4) и (2.5). В настоя­щее время чаще всего используется сигмоидальная функция, опре­деляемая выражением

«= тг^ * ° ■ ^<2-⁶⁾

1-е

Отметим, что при jS->~ характеристика (2.6) стремится к поро­говой униполярной функции (2.3). В качестве альтернативы применя­ется функция гиперболического тангенса

(2.7)

В этом случае характеристика (2.7) стремится к пороговой би­полярной функции (2.4) при а—>°=. Примеры функции fs модели (2.2) показаны на рис. 2.3.

Дата добавления: 2015-06-04