Тема 6. Показатели вариации

План

1. Показатели размера и интенсивности вариации

2. Показатели формы распределения

3. Нормальное распределение и его свойства

1.

Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако два распределения, имеющие одинаковую среднюю арифметическую, могут значительно отличаться друг от друга по степени рассеяния (вариации) признака.

Слайд 2а. Пример вариации признака Х

Если индивидуальные значения признака ряда мало отличаются друг от друга (пример А), то средняя арифметическая будет достаточно надежной показательной характеристикой типичного уровня в данной совокупности. Если же ряд распределения характеризуется значительным рассеиванием индивидуальных значений признака (пример Б), то средняя арифметическая будет ненадежной характеристикой типичного уровня этой совокупности и ее практическое применение будет ограничено.

Рисунок – Примеры различных типов вариации признака X

Для измерения рассеяния (вариации) признака применяются различные абсолютные и относительные показатели вариации.

К абсолютным показателям вариации относятся следующие.

1) Размах вариации (R) – представляет собой разность между максимальным и минимальным значениями признака в совокупности:

Слайд 2б. Размах вариации

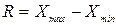
Недостатком данного показателя является то, что он показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов значений признака.

Среднее по совокупности отклонение значения признака от его среднего уровня измеряют два следующих показателя вариации: среднее линейное и среднее квадратическое отклонение.

2) Среднее линейное отклонение (d) – представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической:

Слайд 2в. Среднее линейное отклонение

для несгруппированных данных

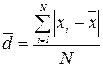
для сгруппированных данных

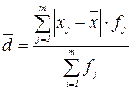
где N – объем совокупности; т – число групп; f_j – частота b j -й группе (y j -гo варианта значения признака).

На практике чаще применяют другой показатель среднего отклонения от средней – среднее квадратическое отклонение.

3) Среднее квадратическое отклонение (s) – представляет собой среднюю квадратическую из отклонений отдельных вариантов от их средней арифметической:

Слайд 3а. Среднее квадратическое отклонение

для несгруппированных данных

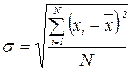
для сгруппированных данных

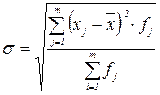
Среднее линейное и квадратическое отклонение показывают, как расположена основная масса единиц совокупности относительно среднего арифметического значения; они выражаются в тех же единицах, что и варианты (X), поэтому экономически хорошо интерпретируются.

4) Дисперсия s² – это квадрат среднего квадратического отклонения. Она представляет собой средний квадрат отклонений вариантов от их средней величины. Для несгруппированных данных:

Слайд 3б. Дисперсия

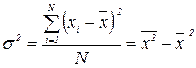
Для сгруппированных данных:

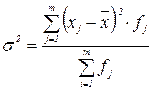
Дисперсия может быть разложена на составные части, позволяющие оценить влияние различных факторов, обусловливающих вариацию признака.

Пусть при группировке совокупности по некоторому признаку X было образовано т однородных групп. Согласно правилу о разложении дисперсии общая дисперсия признака X (s²) (по совокупности в целом) может быть разложена на две составные части:

1) межгрупповую (s_х²);

2) остаточную дисперсию (s_ε²):

Слайд 4а. Разложении дисперсии

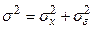
Общая дисперсия рассчитывается по формуле простой дисперсии и показывает величину вариации признака, обусловленную всеми факторами, влияющими на данный признак.

Межгрупповая дисперсия характеризует ту часть общей вариации признака, которая обусловлена делением совокупности на группы. То есть она характеризует вариацию признака, обусловленную факторами, с которыми связано деление совокупности на группы. Поэтому ее еще называют факторной дисперсией. Межгрупповая дисперсия равна среднему взвешенному квадрату отклонений групповых (частных) средних от общей средней:

Слайд 4б. Межгрупповая дисперсия

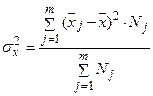
Средняя из внутригрупповых дисперсий (или остаточная) характеризует остаточную вариацию, не связанную с группированием. То есть она характеризует вариацию признака, обусловленную прочими факторами, не связанными с делением совокупности на группы. Вычисляется она как средняя взвешенная из внутригрупповых дисперсий:

Слайд 4в. Остаточная дисперсия

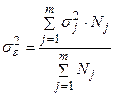
где s_j² – дисперсия признака внутри j -й группы.

Чем больше межгрупповая дисперсия, тем лучше проведена группировка, поэтому она является критерием группирования для группировок с одинаковым числом групп. Лучшей будет та группировка, у которой величина межгрупповой дисперсии больше.

Основные вычислительные свойства дисперсии:

1) дисперсия постоянной величины равна 0;

2) если все варианты значений признака уменьшить на одно и то же число, то дисперсия не изменится;

3) если все варианты значений признака уменьшить в одно и то же число А раз, то дисперсия уменьшится в А² раз.

Относительные показатели вариации применяют, если необходимо оценить интенсивность вариации, или сравнить вариацию признака в различных совокупностях, или сравнить вариацию различных признаков. Показатели относительной вариации рассчитывается как отношение абсолютных показателей вариации (рассмотренные ранее) к средней арифметической величине признака.

1) относительный размах вариации (l):

Слайд 5а. Относительный размах вариации

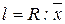
2) относительное отклонение по модулю (h)

Слайд 5б. Относительное отклонение по модулю

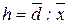
3) коэффициент вариации (v)

Слайд 5в. Коэффициент вариации

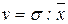
Коэффициент вариации используют также как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.

2.

К показателям формы распределения относят показатель симметричности и островершинности распределения.

1) Показатель симметричности распределения – коэффициент асимметрии.

Симметричным является распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных одновершинных распределений средняя арифметическая, мода и медиана равны между собой. Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии, отрицательная – на наличие левосторонней асимметрии.

Слайд 6а. Виды ассиметрии

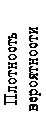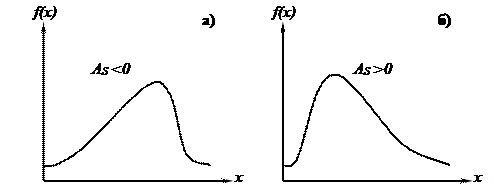Рисунок – Виды ассиметрии:

а) – левосторонняя; б) – правосторонняя

Существуют различные способы расчета коэффициента асимметрии:

Слайд 6б. 1-й способ расчета коэффициента ассиметрии

1. .

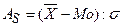Величина As может изменяться от -1 до +1 (для одновершинных распределений). Чем ближе по модулю As к 1, тем асимметрия существеннее.

2. Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка (в симметричном распределении его величина равна нулю):

Слайд 6в. 2-й способ расчета коэффициента ассиметрии

.

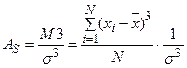Для оценки существенности такого коэффициента асимметрии вычисляется показатель средней квадратической ошибки коэффициента асимметрии:

Слайд 6г. Оценка существенности коэф-та ассиметрии

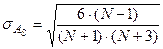
Отношение 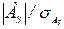, дающее значение, большее 3, свидетельствует о существенном характере асимметрии.

2) Показатель островершинности распределения – эксцесс.

Эксцесс (Ех) представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Он рассчитывается для симметричных распределений. Наиболее точным является показатель, использующий центральный момент четвертого порядка (М4):

Слайд 7а. Эксцесс

.

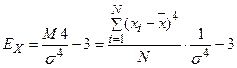(для нормального распределения отношение М 4 /s⁴ =3, следовательно, эксцесс равен нулю). Наличие положительного эксцесса означает, что распределение более островершинное, чем нормальное; отрицательное значение эксцесса означает более плосковершинный характер распределения, чем у нормального.

Слайд 7б. Эксцесс распределения

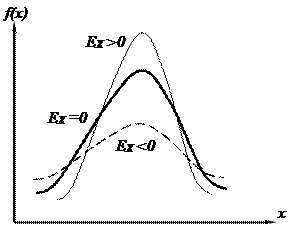Рисунок – Эксцесс распределения

3.

Нормальное распределение может быть представлено графически в виде симметричной куполообразной кривой.

Слайд 8а. Кривая нормального распределения

Куполообразная форма кривой показывает, что боль­шинство значений концентрируется вокруг центра измерения. Уравнение нормальной кривой:

Слайд 8б. Уравнение нормальной кривой

,

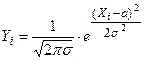где Y_i – ордината кривой нормального распределения; π= 3,1415 и е =2,7182 – математические константы; а – математическое ожидание X (для статистической совокупности 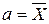); s – среднее квадратическое отклонение.

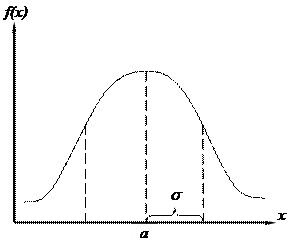Рисунок – Нормальное распределение

Основные особенности кривой нормального распределения:

1. Кривая симметрична относительно максимальной ординаты, которая соответствует значению х=Mo=Me= 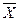, ее величина равна

Слайд 9а. Кривая симметрична относительно макс. ординаты

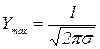
2. Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. Следовательно, чем больше значения отклоняются от X, тем реже они встречаются.

3. Кривая имеет 2 точки перегиба, находящиеся на расстоянии 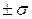от .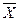

4. При X = const с увеличением s кривая становится более пологой. При s= const с изменением 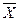кривая не меняет свою форму, а лишь сдвигается вправо или влево по оси абсцисс.

5. В промежутке 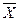± s находится 68,3% всех значений признака. В промежутке 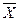±2s находится 95,4% всех значений признака. В промежутке 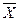±3s находится 99,7% всех значений признака.

6. Параметры нормального распределения: Mo=Me= 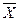, As=0, Ex = 0.

7. Нормальное распределение с параметрами а =0 и s =1 называется стандартным нормальным распределением.

В вариационных рядах существует определенная связь между изменениями частот и значений варьирующего признака. Такого рода изменения называются закономерностями распределения. Для дискретного признака имеет место зависимость частостей (играющих роль вероятностей) от значения признака X. Для непрерывного признака – зависимость между плотностями распределения частот и значениями признака.

Наиболее широкое практическое использование получили следующие виды распределений.

Для дискретного признака:

• распределение Пуассона;

для непрерывного признака:

• нормальное распределение;

• экспоненциальное распределение.

Фактические закономерности отражают ряды распределения, а графически оно представляется с помощью полигона и гистограммы распределения. Фактическое распределение отличается от теоретического, тем что связано с влиянием случайных факторов. Их влияние сглаживается с увеличением объема исследуемой совокупности.

Если отличие между теоретическими и эмпирическими частотами небольшое, то можно считать, что признак X распределен по данному теоретическому закону. Объективную оценку близости эмпирических частот к теоретическим можно получить с помощью определенных критериев согласия. Существует множество таких критериев.

Наиболее широкое распространение получил критерий согласия «хи-квадрат» (или критерий Пирсона). Данный критерий применяется для сгруппированных данных. Он представляет собой случайную величину, имеющую распределение, близкое к распределе­нию «хи-квадрат», которую определяют по формуле:

Слайд 9б. Критерий согласия «хи-квадрат»

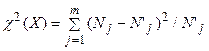
где т – число групп;

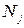– эмпирическая частота в j -й группе;

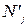– теоретическая частота в j -й группе.

Если расхождение между сравниваемыми эмпирическими и теоретическими частотами распределения окажется слишком большим, т. е. 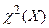будет принимать большие численные значения, то считают, что эмпирическое распределение сильно отличается от теоретического. А если расхождение окажется небольшим, то предполагают, что эмпирическое распределение близко к теоретическому.

Оценку существенности величины 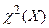можно получить, сравнив вычисленное по наблюдаемым данным значение критерия с табличным (критическим) значением – 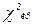. Если 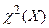< 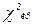, то считают, что отличие фактического распределения от теоретического несущественно; а если 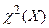> 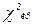, то отличие существенно.

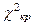определяют по статистическим таблицам значений -критерия Пирсона в зависимости от уровня значимости a (вероятности того, что в наших выводах будет допущена ошибка) и параметра k, который равен: k=m-h-1, где h – число оцененных параметров теоретического распределения по наблюдаемым значениям признака.

Если проверяется гипотеза для дискретного ряда распределения, то порядок расчета 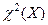следующий:

1) строится эмпирический ряд распределения и находятся эмпирические частоты 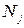. При этом может оказаться, что для некоторых групп 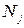<5 (обычно в начале или конце ряда). Такие группы следует объединить с соседними, чтобы условие 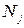>5 выполнялось для всех групп;

2) рассчитываются теоретические вероятности 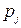; для объединенных групп соответствующие вероятности суммируются. Если параметры теоретического распределения неизвестны, то их оценивают по наблюдаемым значениям признака (например, методом максимума правдоподобия);

3) вычисляются ожидаемые частоты: 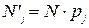, где N – объем совокупности;

4) вычисляется значение критерия «хи-квадрат» по формуле.

Дата добавления: 2015-06-26