Будем предполагать, что функция и(х, у, z) непрерывна и имеет непрерывные производные по своим аргументам в области D

Производная по направлению. Градиент

Рассмотрим в области D функцию и = и (х, у, z) и точку М (х, у, z). Проведем из точки М вектор S, направляющие косинусы которого cos a, cos b, cos g (рис. 5). На векторе S на расстоянии D s от его начала рассмотрим точку М ₁(х + D х, у + D у, z + D z). Таким образом,

z

.

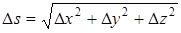Полное приращение функции представим так:

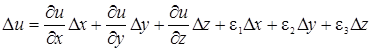, (36)

где e₁, e₂ и e₃ стремятся к нулю при D s ® 0. Разделим все члены равенства (36) на D s:

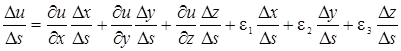. (37)

Очевидно, что

, , .

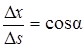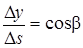Следовательно, равенство (37) можно переписать так:

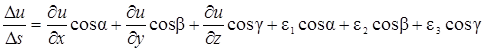. (38)

Предел отношения при D s ® 0 называется производной от функции и = и (х, у, z) в точке (х, у, z) по направлению вектора S и обозначается , т.е.

.

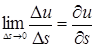Таким образом, переходя к пределу в равенстве (38), получим

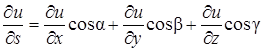. (39)

Из формулы (39) следует, что, зная частные производные, легко найти производную по любому направлению S. Сами частные производные являются частным случаем производной по направлению. Так, например, при a = 0, , 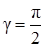получаем:

.

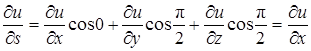Пример 37. Дана функция . Найти производную в точке М (1, 1, 1) в направлении вектора S = 2 i + j + 3 k.

Находим направляющие косинусы вектора S:

, , .

Следовательно,

.

Частные производные

, ,

в точке М (1, 1, 1) будут

, , .

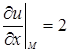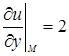Итак,

.

В каждой точке области D, в которой задана функция u = u (x, y, z), определим вектор, проекциями которого на оси координат являются значения частных производных 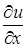, , этой функции в соответствующей точке:

.

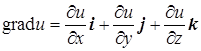Этот вектор называется градиентом функции u (x, y, z). Говорят, что в области D определено векторное поле градиентов. Докажем, следующую теорему, устанавливающую связь между градиентом и производной по направлению.

Теорема. Пусть дано скалярное поле и = u (x, y, z) и определено в этом скалярном поле поле градиентов

.

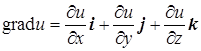Производная по направлению некоторого вектора S равняется проекции вектора grad и на вектор S.

Доказательство. Рассмотрим единичный вектор S ⁰, соответствующий вектору S:

S ⁰ = i cos a + j cos b + k cos g.

Вычислим скалярное произведение векторов grad и и S ⁰:

.

Выражение, стоящее в правой части этого равенства, есть производная от функции u (x, y, z) по направлению вектора S. Следовательно, мы можем написать

.

Если обозначим угол между векторами grad и и S ⁰ через j (рис. 6), то можно написать

(40)

или

.

Теорема доказана.

На основании доказанной теоремы наглядно устанавливается связь между градиентом и производной в данной точке по любому направлению. В данной точке М (х, у, z) строим вектор grad и (рис. 7). Строим сферу, для которой grad и является диаметром. Из точки М (х, у, z) проводим вектор S. Обозначим точку пересечения вектора S с поверхностью сферы через Р. Тогда очевидно, что МР = |grad u | cosj, если j - угол между направлениями градиента и отрезка МР (при этом 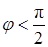), т.е. . Очевидно, что при изменении направления вектора S на противоположное производная изменит знак, а ее абсолютная величина останется прежней.

Установим некоторые свойства градиента.

1. Производная в данной точке по направлению вектора S имеет наибольшее значение, если направление вектора S совпадает с направлением градиента; это наибольшее значение производной равно |grad u |.

Справедливость этого утверждения непосредственно следует из равенства (40): наибольшее значение будет при j = 0, и в этом случае

.

2. Производная по направлению вектора, перпендикулярного к вектору grad и, равна нулю.

Это утверждение следует из формулы (40). Действительно, в этом случае

, cos j = 0 и .

Пример 38. Дана функция и = х ² + у ² + z ².

Определим градиент в точке М (1, 1, 1). Выражение градиента этой функции в произвольной точке будет

grad u = 2 x i + 2 y j + 2 z k.

Следовательно,

grad u | _M = 2 i + 2 j + 2 k, .

Определим производную от функции и в точке М (1, 1, 1) в направлении градиента. Направляющие косинусы градиента будут

, , .

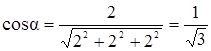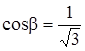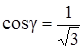Следовательно,

,

т.е.

.

Замечание. Если функция и = и (х, у) есть функция двух переменных, то вектор

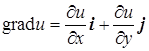
лежит в плоскости Оху. Докажем, что grad и направлен перпендикулярно к линии уровня и (х, у) = с, лежащей в плоскости Оху и проходящей через соответствующую точку. Действительно, угловой коэффициент k ₁ касательной к линии уровня и (х, у) = с будет равен 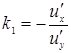. Угловой коэффициент k ₂ градиента равен . Очевидно, что k ₁ k ₂ = -1. Это и доказывает справедливость нашего утверждения. Аналогичное свойство имеет градиент функции трех переменных.

Пример 39. Определить градиент функции 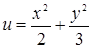в точке М (2, 4).

Здесь 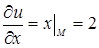, 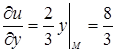. Следовательно,

grad u = 2 i + j.

Дата добавления: 2015-06-04