Примеры для самостоятельной работы

Приложения двойных интегралов к механике

Примеры для самостоятельной работы

Изобразить на чертежах и найти площади частей следующих поверхностей:

97. Конуса z² = 2 xy, отсекаемого плоскостями х + у = а, х = 0, у = 0;

98. Цилиндра x² + y² = R², отсекаемого плоскостями z = 0, z = kx;

99. Плоскости x + y + z = 2 a, вырезаемой цилиндром х² + у² = а²;

100. Гиперболического параболоида z = xy (x > 0, y > 0), вырезаемого цилиндром х² + у² = R²;

101. Конуса y² + z² = x², отсекаемого цилиндром х² + у² = а²;

102. Параболоида y² + z² = 2 x, отсекаемого параболическим цилиндром у² = х и плоскостью х = 1.

Вычислить площади частей поверхностей:

103. 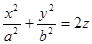внутри цилиндра ;

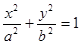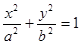104. внутри цилиндра (при z ³ 0);

105. Найти площадь части поверхности параболоида вращения 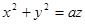, ограниченной плоскостью z = 2 a;

106. Найти площадь части поверхности , содержащейся внутри конуса ;

107. Вычислить площадь поверхности тела, являющейся общей частью двух цилиндров , .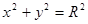

Масса и статические моменты пластинки*. Если D – область плоскости Оху, занятая пластинкой, а g (х, у) – поверхностная плотность пластинки в точке Р(х, у), то ее масса М выражается формулой

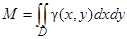, (38)

а статические моменты М_х и М_у относительно осей Ох и Оу определяются двойными интегралами:

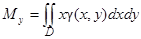, . (39)

Если пластинка однородна, то g (х, у) = const; эту постоянную часто полагают равной единице.

Координаты центра тяжести пластинки. Если С(х₀, у₀) – центр тяжести пластинки, то

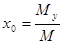, , (40)

где М – масса пластинки; М_х, М_у – ее статические моменты относительно осей координат, определяемые соответственно формулами (38) и (39).

Если пластинка однородна, то то g (х, у) = const. Тогда формулы (40) с учетом формул (38) и (39) принимают вид

, . (41)

(В формулах (41) знаменатели дробей – площадь пластинки, центр тяжести которой отыскивается.)

Моменты инерции пластинки относительно осей Ох и Оу соответственно определяются формулами:

, . (42)

Момент инерции пластинки относительно начала координат

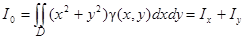. (43)

Полагая g (х, у) = 1 в формулах (42) и (43), получаем геометрические моменты инерции плоской фигуры.

Координаты центра тяжести тела. Если C(x₀, y₀, z₀) – центр тяжести однородного вертикального цилиндрического тела, имеющего своим основанием область D на плоскости Оху и ограниченного поверхностью z = f(x, y), то

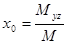, , , (44)

где М – масса тела; М_хy, М_уz, M_xz – его статические моменты относительно плоскостей Oxy, Oyz, Oxz, определяемые формулами:

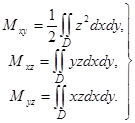(45)

Моменты инерции цилиндрического тела. Моменты инерции цилиндрического тела, ограниченного поверхностью z = f(x, y), ее проекцией D на плоскость Оху и проектирующим цилиндром с образующими, параллельными оси Oz, относительно этой оси и относительно плоскостей Ozx, Oyz выражаются формулами:

; (46)

, . (47)

При вычислении двойных интегралов в формулах (38)-(47) во многих случаях целесообразно перейти к полярным координатам.

Пример 42. Найти массу круглой пластинки радиуса R, если поверхностная плотность g (х, у) материала пластинки в каждой точке Р(х, у) пропорциональна расстоянию точки Р от цента окружности.

Начало прямоугольной декартовой системы координат поместим в центр круга. Тогда координаты любой его точки удовлетворяют соотношению х² + у² £ £ R². Расстояние точки Р(х, у) до начала координат определяется формулой 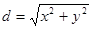, поэтому в соответствии с условием , где k – коэффициент пропорциональности.

По формуле (38) 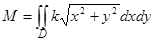, где D – круг х² + у² £ R².

Переходя к полярным координатам, находим

.

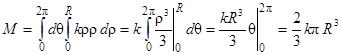Пример 43. Найти статические моменты М_х и М_у фигуры, лежащей в первой четверти, ограниченной эллипсом и координатными осями, если в каждой точке фигуры плотность пропорциональна произведению координат этой точки.

По условию g (х, у) = kху, где k – коэффициент пропорциональности, поэтому формулы (39) для данного случая примут вид

, ,

где D – область, ограниченная дугой эллипса 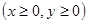и координатными осями.

Найдем сначала статический момент данной фигуры относительно оси Ох:

.

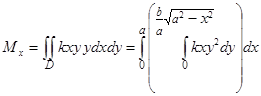Так как 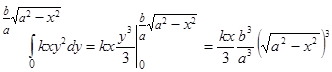, то

Аналогично находим статический момент фигуры относительно оси Оу:

Пример 44. Найти центр тяжести фигуры, указанной в примере 43.

Координаты центра тяжести плоской фигуры определяются формулами (40). Статические моменты М_х, М_у найдены в примере 43, осталось вычислить массу данной фигуры.

По формуле (38)

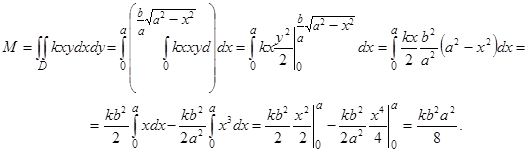
Так как , , то по формулам (40)

, .

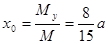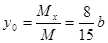Пример 45. Найти центр тяжести однородной фигуры, ограниченной параболой у² = 4 ах + 4 а² и прямой у = 2 а – х.

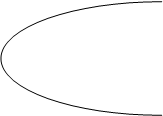
Воспользуемся формулами (41), для чего вычислим предварительно входящие в них двойные интегралы. Найдем интеграл, стоящий в знаменателе; он выражает площадь данной фигуры. Решая совместно уравнения у² = 4 ах + 4 а², у = 2 а – х, находим точки А (0, 2 а), В (8 а, -6 а) пересечения параболы и прямой (рис. 51).

-6а

		Рис. 52
	Рис. 51

В области АВС при фиксированном у х меняется от 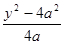(абсцисса точки М) до 2 х – у (абсцисса точки N; выражения для абсцисс точек М и N получены из уравнений линий решения относительно х), а у меняется от –6 а (ордината точки В) до 2 а (ордината точки А). Следовательно,

.

Вычисляем интегралы, стоящие в числителе формул (41):

.

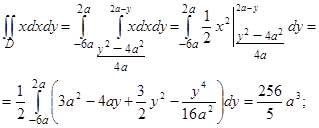
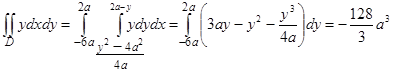По формулам (41) находим координаты центра тяжести:

, .

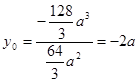Пример 46. Найти моменты инерции однородной полукруглой пластинки 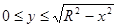относительно осей Ох и Оу.

По первой из формул (42), полагая g(х, у) = 1, находим момент инерции относительно оси Ох:

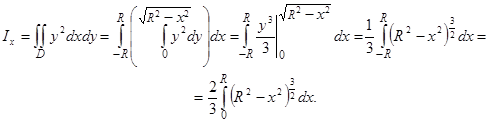
Полученный интеграл вычислим с помощью подстановки :

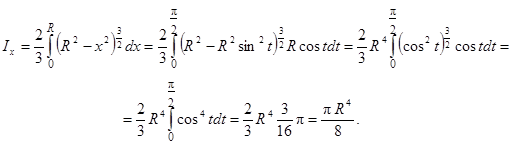
Аналогично вычисляется момент инерции относительно оси Оу:

Итак, , .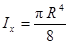

Пример 47. Найти момент инерции однородного лепестка лемнискаты относительно начала координат.

Полагая g(х, у) = 1, по формуле (43) получаем 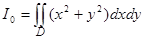, где D – область, ограниченная одной петлей (х ³ 0) лемнискаты (х² + у²) ² = 2 а² (х² – у²).

Для вычисления интеграла перейдем к полярным координатам по формулам х = r cosq, у = r sinq. Так как полярное уравнение лемнискаты имеет вид , а х² + у² = r ² и J (r, q) = r, то

Пример 48. Найти момент инерции однородной фигуры, ограниченной параболой у² = ах и прямой х = а, относительно прямой у = - а.

Формулами (42) здесь пользоваться нельзя, так как прямая у = -а не является координатной осью. Введем новую систему координат, для которой прямая у = -а будет осью О₁Х, ось О₁Y совпадает со старой осью Оу (см. рис. 52). Формулы преобразования: х = Х, у = Y – а, или Х = х, Y = у + а.

В новой системе координат 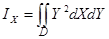, где D – область ОАВ; А (а, а), В (а, -а) – точки пересечения параболы у² = ах и прямой у = х.

В старой системе координат

.

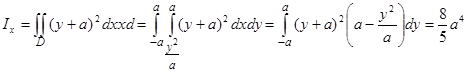Пример 49. Найти центр тяжести однородного тела, вырезанного цилиндром x² + y² = Rx из сферы х² + y² + z² = R².

Из соображений симметрии ясно, что центр тяжести лежит на оси Ох, поэтому у₀ = 0, z₀ = 0. Остается найти координату х₀ с помощью первой из формул (44). Вычислим статический момент тела относительно плоскости Оуz. Третья из формул (45) в данном случае примет вид

,

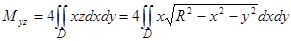где D – полукруг в первом квадранте плоскости Оху, ограниченный линиями х = 0, х² + у² = Rх.

Вычислим этот двойной интеграл, перейдя к полярным координатам по формулам x = r cosq, y = r sinq:

.

Так как

то

Остается вычислить массу тела. Она равна объему V этого тела (тело однородно, поэтому g (x, y, z) = const. Эту постоянную можно положить равной единице).

В силу симметрии

.

Поскольку

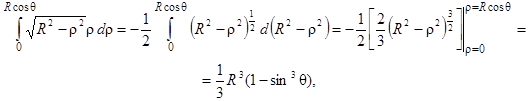
то .

Но ,

поэтому .

Следовательно, .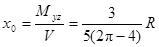

108. Найти массу пластинки, имеющей форму круга радиуса R, если плотность в любой точке Р обратно пропорциональна расстоянию ее до центра круга.

109. Найти массу круговой пластинки радиуса R, плотность которой в каждой точке равна расстоянию этой точки от контура круга.

110. Вычислить массу квадратной пластинки со стороной а, в каждой точке которой плотность пропорциональна сумме ее расстояний до диагоналей квадрата.

111. Пластинка ограничена параболой у² = 2 рх и ее хордой, проходящей через фокус перпендикулярно к оси параболы. Найти массу пластинки, если в каждой точке ее поверхностная плотность обратно пропорциональна расстоянию точки до директрисы параболы.

112. Вычислить массу прямоугольной пластины со сторонами а и b, в каждой точке которой поверхностная плотность пропорциональна квадрату расстояния ее до одной из вершин прямоугольника.

Найти статические моменты относительно осей Ох и Оу однородных пластинок, имеющих формы:

113. Полукруга ;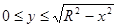

114. Прямоугольника 0 £ х £ а, 0 £ у £ b;

115. Треугольника с вершинами А (0, 0), В (а, 0), С (0, b);

116. Найти статические моменты однородной пластинки, ограниченной эллипсом , координатными осями и лежащей в первой четверти.

Найти центры тяжести однородных пластин, ограниченных линиями:

117. у – х = 0, х + у – 4 = 0, х – 2 у – 4 = 0; 118. у = х², х + у = 2;

119. , х = 0, у = 0; 120. , у = 0;

121. r = 1 + cosq, q = 0; 122. x = t – sin t, y = 1 – cos t (0 £ t £ 2 p), у = 0.

Найти моменты инерции относительно осей координат Ох, Оу однородных пластинок, ограниченных линиями:

123. х = - а, х = а, y = b, y = - b; 124. 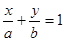, х = 0, у = 0;

125. ; 126. х⁴ + у⁴ = а² (х² + у²);

127. (х - а) ² + (у - а) ² = а², х = 0, у = 0 (0 £ х £ а);

128. ху = а², ху = 2 а², х = 2 у, 2 х = у (х > 0, у > 0).

Найти моменты инерции относительно начала координат однородных пластинок, ограниченных линиями:

129. ; 130. r = 2 а cosq; 131. r = а (1 - cosq).

Найти центры тяжести однородных тел:

132. Конуса , основание которого лежит в плоскости Оху;

133. Треугольной пирамиды, ограниченной плоскостями х + 2 у – z – 1 = 0, х = 0, у = 0, z = 0;

134. Шарового слоя, заключенного между сферой х² + у² + z² = R² и плоскостями х = а, y = b;

135. Полушара х² + у² + z² £ R², z ³ 0.

* Под пластинкой понимается некоторая замкнутая плоская область, по которой распределена масса плотности g = g (х, у).

Дата добавления: 2015-06-04