Радикальный признак Коши

Иногда удобно пользоваться радикальным признаком, Коши для исследования сходимости знакоположительного ряда. Этот признак во многом схож с признаком Даламбера, о чем говорят его формулировка и доказательство.

Теорема 5.4. Пусть дан ряд (4.1) с положительными членами и существует конечный или бесконечный предел .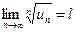

Тогда ряд сходится при 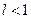и расходится при .

Как и для признака Даламбера, в случае, когда 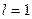, вопрос о сходимости ряда остается открытым. Доказательство теоремы аналогично доказательству признака Даламбера. Поэтому опустим его.

Пример 5.6. Исследовать на сходимость ряд .

Решение: Так как

,

то применим радикальный признак Коши к ряду .

Вычисляем .

Отсюда, ряд сходится, а значит, сходится и исходный ряд, согласно свойству 1 числовых рядов.

5.4. Интегральный признак Коши. Обобщённый гармонический ряд.

Теорема 5.5. Если члены знакоположительного ряда 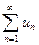могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке 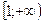функции так, что 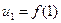, , , …., , …., 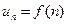то:

1) если сходится, то сходится и ряд (6.1);

2) если расходится, то расходится также и ряд (6.1).

О сходимости несобственных интегралов см. [1], стр.89.

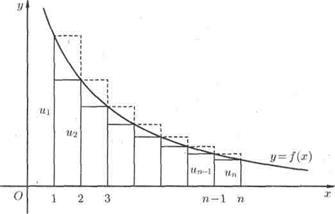
Рис.2

Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции , основанием которой служит отрезок оси Ох от х = 1 до х = 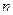(см. рис. 2).

Построим входящие и выходящие прямоугольники, основаниями которых служат отрезки [1; 2], [2;3],... Учитывая геометрический смысл определенного интеграла, запишем:

,

или

,

или 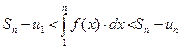. (5.7)

Случай 1. Несобственный интеграл сходится, т. е. .

Поскольку 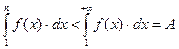, то с учетом неравенства (5.7) имеем: , т. е. . Так как последовательность частичных сумм монотонно возрастает и ограничена сверху (числом ), то, по признаку существования предела, эта последовательность имеет предел. Следовательно, ряд (6.1) сходится.

Случай 2. Несобственный интеграл расходится. Тогда и интегралы 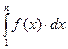неограниченно возрастают при .

Учитывая, что (см. (5.7)), получаем, что 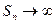при . Следовательно, данный ряд (6.1) расходится.

Замечание. Вместо интеграла можно брать интеграл , где , . Отбрасывание первых членов ряда в ряде (6.1), как известно, не влияет на сходимость (расходимость) ряда.

Пример 5.7. Исследовать на сходимость ряд .

Решение: Воспользуемся интегральным признаком Коши. Функция 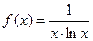удовлетворяет условиям теоремы 5.5. Находим

.

Значит, ряд с общим членом 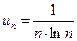расходится.

Ряд

, (5.8)

где 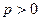- действительное число, называется обобщенным гармоническим рядом. Для исследования ряда (5.8) на сходимость применим интегральный признак Коши (признаки Даламбера и Коши ответа о сходимости не дают).

Рассмотрим функцию . Эта функция непрерывна, монотонно убывает на промежутке и . При имеем:

При 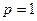имеем гармонический ряд , который расходится (второй способ: ).

Итак, ряд (5.8) сходится при 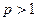, расходится при .

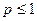В частности, ряд 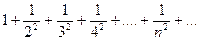сходится (полезно знать).

Рассмотренные признаки сходимости (есть и другие) знакоположительных рядов позволяют судить о сходимости практически любого положительного ряда. Необходимые навыки приобретаются на практике.

Дата добавления: 2015-06-04