Элементы теории сетей

Лекция № 4

Часто на практике более удобным инструментом исследования сис­тем яв­ляется представление их в виде сетей. Сеть - это естественное об­об­щение по­ня­тия граф.

Def. Множество 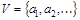и набор , в ко­то­ром каждое есть набор элементов из V, т.е. , на­зы­ва­ет­ся сетью и обозначается .

Объекты множества V называются вершинами, а объекты из набо­ра - полюсами сети.

В литературе встречается понятие "суперграф", которое отли­чает­ся от по­ня­тия "сеть" незначительными деталями.

В случае, когда множество V и набор W конечны, сеть называется конеч­ной. Сеть, в которой бесконечно V или W, называется бесконеч­ной. Ограни­чим­ся рассмотрением конечных сетей.

Пусть 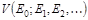- сеть. Если E - набор, то через <E> обозна­чают множество всех элементов из E. Множество V можно разбить на три непере­се­каю­щиеся части:

V1 = < > - множество полюсов;

- множество изолированных вершин, не попавших ни в один набор (i = 0, 1, 2,...);

V3 - прочие вершины.

Подобно тому, как это было сделано в случае графов, можно ввес­ти поня­тие геометрической реализации для сети.

В трехмерном евклидовом пространстве каждой вершине из V1 и V2 со­пос­тавим точку так, чтобы различным вершинам соответствовали раз­лич­ные точки. Эти точки пометим символами соответствующих вер­шин 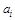. Каждому набору из W (i>=1) сопоставим круг (если со­дер­жит один или два объекта, то вместо круга можно взять вершину или дугу). Круги должны попарно не пересекаться. На круге, соот­вет­ст­вую­щем набору , поместим точ­ки, соответствующие вершинам 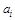дан­ного набора. Затем все точки, поме­чен­ные одним и тем же символом 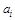из V, соединяются связной компонентой . Дополнительно по­тре­буем, чтобы связная компонента с построенными ра­нее вершинами и кругами имела общими только точки, помеченные символом 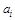, и чтобы связные компоненты и не имели общих точек. Полученную фигуру будем называть геометрической реализацией сети.

При таком подходе для каждой сети в трехмерном пространстве су­щест­вует геометрическая реализация.

Пример.

Пусть

V = {1, 2, 3, 4, 5, 6, 7}, ,

= (1, 2, 6), 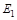= (1, 3, 3, 4, 5),

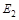= (4, 4, 4, 5, 6), (2, 4),

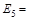(2, 5, 6, 7).

Тогда 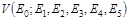- сеть.

Студентам предлагается самостоятельно построить геометри­чес­кую реа­лизацию этой сети.

Геометрическая реализация сетей по внешнему виду напоминает схе­му ком­муникаций или радиосхему, в которой условные знаки от­дель­ных эле­мен­тов заменены кругами. Это не случайно, так именно в этих об­лас­тях сети наи­бо­лее часто используются.

Рассмотрим некоторые классы сетей, наиболее часто встречаю­щие­ся на практике.

I. Класс сетей, у которых - пустое множество, а каждый набор 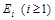состоит из двух объектов множества V, совпадает с классом графов.

II. Дерево - конечный связный не содержащий циклов граф с вы­деленной вершиной, именуемой корнем.

Дерево - однополюсная сеть, т.е. . Дерево всегда допус­кает гео­мет­ри­ческую реализацию на плоскости. Геометрическая реали­за­ция де­ре­ва, в кото­рой ребра представ­ляют отрезки прямых, а корень изо­бра­жен вершиной с до­пол­нительным отрезком - стрелкой, называется уклад­кой дерева.

Пример.

Пусть

V = {0, 1, 2,..., 10}, ,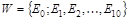

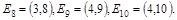
Тогда - дерево.

Возможны несколько вариантов укладки дерева. Если двигаться по дереву от корня к концевым вершинам, можно осуществить ориен­та­цию ребер дерева. При этом в каждую вершину входит некоторое ребро и из каж­дой вершины (кро­ме концевой) исходит несколько ребер. Мож­но упо­рядочить исходящие ребра в каждой вершине, например, в по­рядке их следования, двигаясь от вхо­дящего ребра по часовой стрелке.

Естественно считать, что две укладки одного дерева одинаковы, ес­ли по­рядки следо­вания исходящих ребер для соответствующих вершин совпадают.

III. Двухполюсные сети из двухобъектных наборов.

Данный класс совпадает с классом конечных графов, в каждом из ко­торых выделены две вершины - полюса. Такие сети обозначают

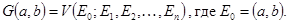
Для таких сетей, как и для графов, вводится понятие пути, соеди­няю­щего некоторые его вершины 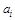и . Если 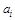= a, а = b, где a и b - полюса, то употребляется термин путь без указания вершин, которые он соединяет.

Сеть называется связной, если соответствующий граф связный.

Таким образом, сеть связна, если для каждого ребра можно ука­зать путь, проходящий через него.

Пусть в сети взяты два пути и , соеди­няю­щие вер­шины c и d. Путь называется подпутем пути , если получается путем удаления некоторого подмножества ребер из пути .

Путь сети , называется цепью, соединяющей эти вер­ши­ны, ес­ли он не содержит подпутей. Если вершины цепи c и d сов­па­да­ют с по­лю­сами сети, то вместо слов "цепь, соединяющая a и b ", гово­рят просто "цепь".

Путь является цепью тогда и только тогда, когда он не проходит дважды ни через одну вершину.

Как мы видим, вводимое в теории сетей понятие "цепь" эквива­лент­но вве­ден­ному нами понятию "путь" в теории графов.

Подробнее с теорией графов и сетей можно ознакомиться в лите­ра­ту­ре по дискретной математике.

Дата добавления: 2015-06-04