Принципы анализа эффективности нерекурсивных алгоритмов

Основные классы эффективности

Ограниченность показателя функции роста

Пусть даны две программы, время выполнения одной O(n²), а вторая O(n³), причем при определенной комбинации компилятора ПК одна программа выполнятся за 100n², а вторая 5n³ может ли быть вторая программа предпочтительней другой? При n < 20, вторая функция предпочтительнее, т.к. для ее выполнения требуется меньше операций: 5n³ < 100n². Однако, при n > 20 первая программа становится предпочтительней. Вообще выбор определяется между программами на основе оценки трудоемкости и по возможности выбирается функция с полиномом меньшей степени. Чем меньше степень роста, тем больше размер задачи, которую можно решить на компьютере. Рассмотрим два случая использования этих алгоритмов: пусть в первом случае для решения задачи выделено машинное время T1 = 10000 мс, а во тором – в 100 раз больше (см таблицу).

Таблица

Функция трудоемкости решения задачи, f (n)	T 1 = 10000 мс	T 2 = 100*10000	затрат в 100 раз выше
Размерность задачи, решаемой за время T 1 и T 2
n 1	n 2
100 n ²			рост размерности задачи в 10 раз
5 n ³			в 5 раз

То есть, если выделено T ₁ времени на ЭВМ для решения задачи этими алгоритмами, тогда мы успеем решить задачу размерности 10. Заплатив за время в 100 раз больше, и получив время в 100 раз больше, мы можем за новое время решить задачу размерности 100 и 60.

Вывод: увеличивая время выполнения на прежних ПК эффективность решаемой задачи (размерность) уменьшается и возможна ситуация, когда на увеличение размерности хотя бы на единицу потребуется времени неизмеримо много.

Увеличение времени соответствует увеличению производительности ЦП (центрального процессора) от версии к версии. Однако существуют такие задачи с такими функциями роста, производительность процессов которых слабо влияет.

Практически вычислимыми, т.е. реализуемыми за приемлемое время являются алгоритмы полиномиального класса трудоемкости – это алгоритмы для которых асимптотическая оценка функции роста трудоемкости алгоритма представляет собой полином некоторой степени O(f (n)) = n^k, где k – константа.

Рассмотрим основные классы алгоритмов на основе вида их функции роста.

В теории анализа эффективности алгоритмов к одному классу относят все функции, чей порядок роста одинаков с точностью до постоянного множителя. Рассмотрим их более подробно.

Класс трудоемкости	Вид функции трудоемкости	Название подкласса	Примечание	Пример алгоритма данного подкласса
Полиномиальный класс (Р -класс)	const		Алгоритм не зависит от длины входных параметров, то есть число операторов постоянно и не измениться не при каком случае.
log n	логарифмический	Обычно такая зависимость появляется в результате сокращения размера задачи на постоянное значение на каждом шаге итерации алгоритма. Обратите внимание, что в логарифмическом алгоритме исключается работа со всеми входными данными	Алгоритм бинарного поиска (метод деления отрезка пополам) среди n элементов.
n	Линейная	К этому подклассу относятся алгоритмы, выполняющие сканирование списка, состоящего из n элементов.	Поиск элемента массива из n методом последовательного перебора
	«n - логарифм n»	К этому подклассу относятся большое количество алгоритмов декомпозиции, где для каждого из n элементов необходимо применить эффективный (например) поиск за логарифмическое время	Эффективные алгоритмы сортировки: пирамидальная, фиксированное двухпутевое слияния
n ^2	Квадратичная	подобная зависимость характеризует эффективность алгоритмов, содержащих два вложенных цикла, каждый из которых выполняется не более n раз	Простые схемы сортировки, например, пузырьковая,
	Кубическая	Как правило, подобная зависимость характеризует эффективность алгоритмов, содержащих три вложенных цикла	Простой алгоритм перемножения матриц
Не детерминировано-полиномиальный (NP -класс)		Экспоненциальная	Данная зависимость типична для алгоритмов, выполняющих обработку всех подмножеств некоторого множества, состоящего из n элементов.	Задача о ханойских башнях.
n!	Факториальная	Данная зависимость типична для алгоритмов, выполняющих обработку всех перестановок некоторого множе­ства, состоящего из n элементов	Полный перебор всех сочетаний элементов исходного множества при поиске решения задачи.
Часто термин "экспоненциальный" используется в широком смысле (в том числе и для всего класса) и означает очень высокие порядки роста, имеющий принципиально другой характер поведения по сравнению с полиномом некоторой степени.

Для примера приведем числа, иллюстрирующие скорость роста для нескольких функций, которые часто используются при оценке временной сложности алгоритмов (см. Таблица 1).

Таблица 1

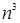
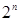
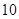
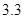
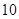
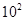
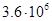
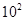
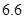
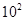
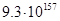
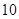
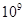
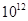
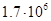
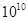
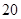
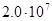
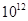
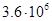
Порядок чисел, приведенных в таблице, имеет чрезвычайное значение для анализа алгоритмов. Как видно из таблицы, самый малый порядок роста имеет логарифмическая функция. Причем его значение настолько мало, что программы, реализующие алгоритмы с логарифмическим количеством основных операций, будут выполняться практически мгновенно для всех диапазонов входных данных реального размера, причем вне зависимости от основания логарифма, так как переход от одного основания к другому есть константа:

log _a n = log_a b log _b n.

Поэтому далее будем опускать основание логарифма, то есть log n.

Если считать, что числа соответствуют микросекундам, то для задачи с 1048476 элементами алгоритму со временем работы T (log n) потребуется 20 микросекунд, а алгоритму со временем работы T (n ²) – более 12 дней.

Существует и другая крайность: показательная функция 2ⁿ и функция n! – вычисление факториала. Обе эти функции имеют настолько высокий порядок роста, что его значение становится астрономически большим уже при умеренных зна­чениях n. Например, чтобы выполнить 2¹⁰⁰ операций компьютеру, имеющему производительность в один триллион операций в секунду, понадобиться без малого 4 • 1010 лет! Однако это ничто по сравнению со временем, которое затратит тот же компьютер на выполнение 100! операций.

Подводя итог, отметим: c помощью алгоритмов, в которых количество выполняемых операций растет по экспоненциальному закону, можно решить лишь задачи очень малых размеров.

Именно для этого и следует на практике оценивать трудоемкость разрабатываемого алгоритма.

Общий план анализа эффективности нерекурсивных алгоритмов:

1. Выбрать параметр (или параметры), по которому будет оцениваться размер входных данных алгоритма (например, число элементов массива).

2. Определить основную операцию алгоритма. (Как правило, она находится в наиболее глубоко вложенном внутреннем цикле алгоритма.) В ряде источников рекомендуется выбрать базовое множество операций (назовем их основными элементарными операциями, так будем полагать, что каждая из них выполняется за 1 машинный такт, то есть её трудоемкость равна 1), число выполнений которых и будет оцениваться функцией роста трудоемкости алгоритма. К ним отнесем операции

– присваивания;

– арифметические операции (+, –, *, /, div (деление нацело), mod (получение остатка от деления и т.д.);

– операции сравнения (>, <, =, <>, <=, >=);

– логические связки (операции) (and, or, xor, not);

– взятие (получение, использование) адреса ячейки памяти: [] – (в массиве), @ (в паскале – получение адреса), ^ – (в паскале – переход по адресу, * (разыменовывание в Си), & (передача адреса в Си);

– в методических целях также будем полагать, что все библиотечные функции (и процедуры) также имеют трудоемкость, равную 1, если иное особо не оговаривается.

3. Проверить зависимость числа выполняемых основных операций только от размера входных данных. Если оно зависит и от других факторов, рассмотреть при необходимости изменение эффективности алгоритма для наихудшего, среднего и наилучшего случаев.

4. Записать сумму, выражающую количество выполняемых основных операций алгоритма в последовательно исполняемых фрагментах программы.

5. Используя стандартные формулы и правила суммирования (приводимые ниже), упростить полученную формулу для количества основных/элементарных операций алгоритма. Таким образом, получаем функцию роста. Если это невозможно, следует определить, хотя бы, порядок ее роста.

Теоретическая оценка временной сложности алгоритма осуществляется с использованием следующих базовых принципов оценки сложности выполнения основных алгоритмических конструкций:

1. Время выполнения операторов присваивания, чтения и записи обычно имеет порядок О(1), как всякий линейный оператор, кроме случаев использования внутри них функций и процедур. В этом случае оператор имеет порядок выполнения функции или процедуры.

2. Время выполнения последовательности операторов определяется с помощью правила сумм. Поэтому степень роста времени выполнения последовательности операторов без определения констант пропорциональности совпадает с наибольшим временем выполнения оператора в данной последовательности.

3. Время выполнения условных операторов состоит из времени выполнения условно исполняемых операторов и времени вычисления самого логического выражения. Время вычисления логического выражения обычно имеет порядок О(1), если условие не содержит вызов функций, трудоемкость которых зависит от n – в этом случае проверка условия есть последовательное выполнение элементарных операций, в том числе и используемой в проверке условия функции (см. пункт 2). Время для всей конструкции if-then-else состоит из времени вычисления логического выражения и наибольшего из времени, необходимого для выполнения операторов, исполняемых при значении логического выражения true (истина) и при значении false (ложь).

4. Время выполнения цикла является суммой времени всех исполняемых итераций цикла, в свою очередь состоящих из времени выполнения операторов тела цикла и времени вычисления условия прекращения цикла (обычно последнее имеет порядок О(1), если не содержит внутри себя функцию от n). Часто время выполнения цикла вычисляется, пренебрегая определением констант пропорциональности, как произведение количества выполненных итераций цикла на наибольшее возможное время выполнения операторов тела цикла. Однако, не следует для циклов перемножать число выполняемых итераций на трудоемкость отдельной итерации, так как в этом случае зачастую не верно определяется количество исполняемых операций (вид функции роста), хотя асимптотическая оценка может оказаться верной. Кроме того, время выполнения каждого цикла, если в программе их несколько, должно определяться отдельно.

5. Для программ, содержащих несколько процедур (функций) (среди которых нет рекурсивных), можно подсчитать общее время выполнения программы путем последовательного нахождения времени выполнения процедур, начиная с той, которая не имеет вызовов других процедур. Так как мы предположили, что все процедуры нерекурсивные, то должна существовать хотя бы одна процедура, не имеющая вызовов других процедур. Затем можно определить время выполнения процедур, вызывающих эту процедуру, используя уже вычисленное время выполнения вызываемой процедуры. Продолжая этот процесс, найдем время выполнения всех процедур и, наконец, время выполнения всей программы.

6. Если есть рекурсивные процедуры, то нельзя упорядочить все процедуры таким образом, чтобы каждая процедура вызывала только процедуры, время выполнения которых подсчитано на предыдущем шаге. В этом случае мы должны с каждой рекурсивной процедурой связать временн у ю- функцию Т (п), где п определяет объем аргументов процедуры. Затем мы должны получить рекуррентное соотношение для Т (п), т.е. уравнение (или неравенство) для Т(п), где участвуют значения T (k)для различных значений k, то есть Т (п) = F (T (k ₁), T (k ₂), …), k_i < n. После чего Т (п) выражается как функция только от n.

7. Программы с операторами безусловного перехода. При анализе времени выполнения программ мы неявно предполагали, что все ветвления в ходе выполнения процедур осуществлялись с помощью условных операторов и операторов циклов. Мы останавливаемся на этом факте, так как определяли время выполнения больших групп операторов путем применения правила сумм к этом группам. Однако операторы безусловного перехода (такие как goto, досрочный выход из цикла) могут порождать более сложную логическую групповую структуру. Безусловный переход, как правило, либо перемещает выполнение к следующему по порядку следования операторам (например, досрочное завершение цикла и переход к следующему за циклом оператору), либо возвращает к предыдущим, создавая петлю, либо вклинивается в середину группы операторов, запутывая последовательность операторов. Тогда оценка времени выполнения оператора безусловного перехода зависит от способа интерпретации логической структуры группы операторов:

А) Досрочный выход из цикла обычно связан с некоторым условием, тогда оценка определяется по более «длинной» ветви if/then/else, т.е. по полному выполнению цикла, что значительно ухудшает оценку, если существует большая вероятность досрочного завершения цикла.

Б) Возврат к предыдущему фрагменту порождает петлю, которая может быть рассмотрена как новая линейная последовательность операторов. Многократное выполнение петли сводится к циклам или рекурентному выполнению вложенных петель.

В) Отсутствие общего подхода для оценки времени выполнения программы, использующей не приводимое каноническому виду уонструкции с использованием оператора GOTO зачастую исключает возможность оценки времени выполнения такого фрагмента.

В принципе, операторы безусловного перехода можно исключить из программы, заменив их на канонические конструкции структурного программирования.

Дата добавления: 2015-06-04