
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
I. Разложение периодической функции в ряд Фурье
|
|
|
|
Преобразование Фурье
Любую периодическую функцию можно представить суммой отдельных
гармонических составляющих с различными амплитудами A, периодами Т и,
следовательно, частотами ω).
Спектральный анализ заключается в нахождении коэффициентов ak, bk
ряда Фурье
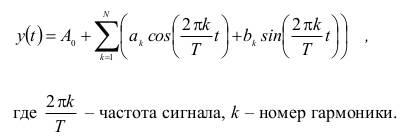
Коэффициенты Фурье определяются выражениями
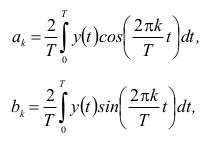
где Т – основной период функции y(t), обычно выбирается близким к
длине ряда.
Задание:
Дискретное преобразование Фурье непериодического сигнала (прямое и обратное)
Код программы:
clear
t=1:11;
z=wgn(1,11,0);
plot(t,z,'r')
Y=fft(z);
yf=ifft(Y);
hold on
grid
plot(t,yf,'*')

Результаты программы:
График зависимости белого шума от t
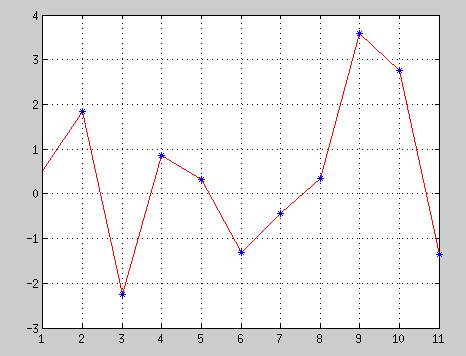
__-шум от t
*-точки,полученные при обратном преобразовании Фурье
Коэффициенты Фурье:
t=1 7,86284003733691 + 0,00000000000000i
2 0,479983818954581 + 1,99292379180807i
3 1,36805687363696 - 3,87106634539110i
4 3,52405246327792 - 0,666879919789640i
5 4,46950437641708 - 2,82136988897207i
6 2,91906151387021 - 0,281542411862946i
7 2,91906151387021 + 0,281542411862946i
8 4,46950437641708 + 2,82136988897207i
9 3,52405246327792 + 0,666879919789640i
10 1,36805687363696 + 3,87106634539110i
11 0,479983818954581 - 1,99292379180807i
Многие явления природы происходят периодически, то есть повторяются в определенном порядке по истечении некоторого промежутка времени, называемого периодом. Математически такие явления описываются с помощью периодических функций.
Пусть  - вещественная функция вещественного аргумента. Функция
- вещественная функция вещественного аргумента. Функция  называется периодической с периодом
называется периодической с периодом 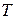 , если она определена на всей вещественной оси и для всех
, если она определена на всей вещественной оси и для всех 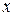 выполняется равенство:
выполняется равенство:
 .
.
Замечание: Если функция  имеет период
имеет период 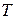 , то она также имеет период
, то она также имеет период 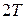 ,
,  , …, то есть
, …, то есть
 .
.
Обычно за основной период принимают наименьшее положительное 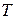 , для которого
, для которого  .
.
Следовательно, полное представление о функции  можно получить, изучив ее на любом интервале длины
можно получить, изучив ее на любом интервале длины 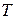 , например:
, например: 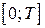 ,
,  ,
,  ,
,  ,…так как
,…так как  принимает одинаковые значения при любых
принимает одинаковые значения при любых 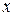 , отличающихся друг от друга на
, отличающихся друг от друга на 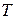 .
.
Изменение функции за период 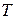 называется ее колебанием.
называется ее колебанием.
Рассмотрим интеграл от периодической функции  :
:  .
.
 Как известно, геометрический смысл определенного интеграла это площадь фигуры, ограниченной функцией
Как известно, геометрический смысл определенного интеграла это площадь фигуры, ограниченной функцией  и осью
и осью  на промежутке
на промежутке 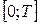 (см. рис.1).
(см. рис.1).
А интеграл 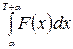 численно равен площади заштрихованной фигуры на рис.2
численно равен площади заштрихованной фигуры на рис.2
 Видно, что площадь фигуры на рис.1 равна площади фигуры на рис.2, следовательно:
Видно, что площадь фигуры на рис.1 равна площади фигуры на рис.2, следовательно:
 ,
,
то есть интегралы по любым отрезкам длины 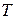 от периодической функции
от периодической функции  с периодом
с периодом 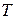 равны.
равны.
С периодическими движениями (колебаниями) приходится иметь дело в самых различных областях знания – в теории упругости, акустике, радиотехнике, электротехнике, теории автоматического управления. В общем случае характер периодического движения может быть очень сложным.
Нужно сказать, что физики давно считали, что всякое сложное периодическое движение точки (сложное колебание) – будь то механическое колебание точки струны или электромагнитное колебание, или колебание, связанное с распространением звука – распадается на гармонические колебания, то есть сложное периодическое движение надо мыслить как сумму (конечную или бесконечную) простых гармонических колебаний того же периода, соответствующих данной частоте k (простейшими периодическими движениями являются гармонические колебания).
Физики такое разложение из реального движения получают при помощи специальных приборов – резонаторов, математики – при помощи вычислений.
Таким представлением периодической функции пользуются, например, в электротехнике: явления, происходящие в электрических цепях с несинусоидальной, периодически меняющейся электродвижущей силой, проще всего поддаются исследованию, если эту электродвижущую силу разложить на сумму гармоник.
Поэтому возникает потребность представления периодической функции в виде суммы более простых периодических функций, в качестве которых используются 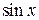 и
и  .
.
С этой целью рассмотрим бесконечную систему тригонометрических функций:
 (1)
(1)
где 1=  и
и 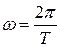 ,
, 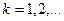
Функции  и
и  являются периодическими с периодом Т:
являются периодическими с периодом Т:
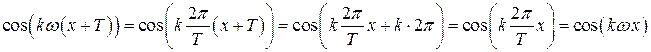 Аналогично для
Аналогично для  .
.
Вообще минимальным периодом для функций  и
и  является
является 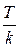 , но тогда и
, но тогда и 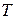 тоже является периодом. Постоянную функцию (константу) можно считать периодической любого периода.
тоже является периодом. Постоянную функцию (константу) можно считать периодической любого периода.
Таким образом, общий период всех функций из бесконечной системы (1) будет равен Т.
Так как функция имеет период 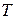 , то это означает, что одно полное колебание происходит за промежуток времени
, то это означает, что одно полное колебание происходит за промежуток времени 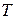 . Количество колебаний в единицу времени это
. Количество колебаний в единицу времени это  , а за
, а за  секунд происходит
секунд происходит  колебаний. Эта величина называется круговой частотой
колебаний. Эта величина называется круговой частотой 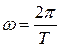 (число колебаний за
(число колебаний за  секунд).
секунд).
Число колебаний в секунду – величина, обратная периоду:  - также называется частотой колебания, ее единицей измерения является герц.
- также называется частотой колебания, ее единицей измерения является герц. 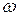 и
и 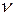 связаны равенством
связаны равенством  .
.
Введенная система тригонометрических функций является ортогональной на промежутке длины 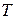 , так как интеграл по отрезку
, так как интеграл по отрезку 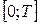 от произведения любых двух различных функций последовательности (1) равен нулю:
от произведения любых двух различных функций последовательности (1) равен нулю:
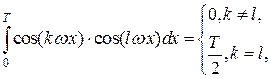

 , при
, при 
Пусть дана периодическая функция  с периодом
с периодом 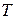 , которая необязательно является тригонометрическим многочленом. С помощью введенной системы тригонометрических функций составим тригонометрический ряд:
, которая необязательно является тригонометрическим многочленом. С помощью введенной системы тригонометрических функций составим тригонометрический ряд:
 , (2)
, (2)
где 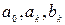 вычисляются по формулам:
вычисляются по формулам:
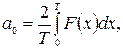


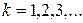
Этот ряд представляет собой частный случай функционального ряда и называется рядом Фурье для  , а
, а 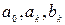 называются коэффициентами ряда Фурье для функции
называются коэффициентами ряда Фурье для функции  .
.
Слагаемое 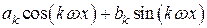 называется
называется  -той гармоникой ряда Фурье.
-той гармоникой ряда Фурье.
Ряд Фурье сходится к функции  только при определенных условиях. Эти условия называются условиями Дирихле. Сформулируем их.
только при определенных условиях. Эти условия называются условиями Дирихле. Сформулируем их.
Функция  удовлетворяет на отрезке
удовлетворяет на отрезке  условиям Дирихле, если:
условиям Дирихле, если:
1)  непрерывна на
непрерывна на  , либо имеет на этом отрезке конечное число точек разрыва I рода.
, либо имеет на этом отрезке конечное число точек разрыва I рода.
2)  монотонна на
монотонна на  , либо имеет на этом отрезке конечное число экстремумов.
, либо имеет на этом отрезке конечное число экстремумов.
Теорема Дирихле: Если функция  с периодом
с периодом 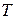 на отрезке длины
на отрезке длины 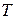 удовлетворяет условиям Дирихле, то:
удовлетворяет условиям Дирихле, то:
1) ряд Фурье для этой функции сходится на всей оси 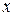 ,
,
2) сумма ряда Фурье равна  во всех точках непрерывности этой функции:
во всех точках непрерывности этой функции: 
 =
=  ,
,
где  -периодическая функция с периодом Т.
-периодическая функция с периодом Т.
3) В точках разрыва I рода функции  сумма ряда равна полусумме левого и правого пределов функции
сумма ряда равна полусумме левого и правого пределов функции  в этих точках.
в этих точках.
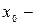 точка разрыва I рода,
точка разрыва I рода, 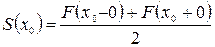
В частности, если на концах отрезка  функция
функция  терпит разрыв, то сумма ряда в этих точках равна:
терпит разрыв, то сумма ряда в этих точках равна: 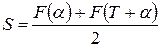
Эта теорема имеет достаточный характер. Если на некотором промежутке  ряд Фурье сходится к функции
ряд Фурье сходится к функции  , то говорят, что на этом промежутке функция
, то говорят, что на этом промежутке функция  разложена в ряд Фурье, и пишут:
разложена в ряд Фурье, и пишут:
 =
=  ,
, 
Пусть  на промежутке
на промежутке  представима функцией
представима функцией 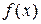 . Тогда ряд Фурье для функции
. Тогда ряд Фурье для функции  совпадает с рядом Фурье для функции
совпадает с рядом Фурье для функции 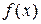 , заданной на промежутке
, заданной на промежутке  .
.
Ряд Фурье в виде  называется рядом Фурье в вещественной форме.
называется рядом Фурье в вещественной форме.
Члены ряда (2) можно записать в виде гармоник: 
Обозначая  , получим
, получим
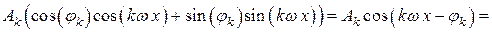
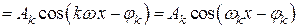 ,
,
где  -
- 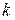 -ая гармоника,
-ая гармоника, 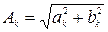 - амплитуда
- амплитуда 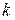 -ой гармоники,
-ой гармоники,  дает наибольшее отклонение точки, движущейся по закону
дает наибольшее отклонение точки, движущейся по закону 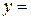
 , от начала координат,
, от начала координат, 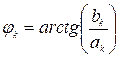 - фаза k-ой гармоники, причем, если при некотором
- фаза k-ой гармоники, причем, если при некотором 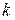
 и
и  , то при таком
, то при таком 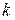 гармоническое колебание не определено,
гармоническое колебание не определено, 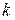 -ая гармоника равна 0 и
-ая гармоника равна 0 и 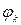 не существует;
не существует;  - частота k-ой гармоники.
- частота k-ой гармоники.
Тогда ряд Фурье для функции  примет вид:
примет вид:
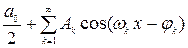 .
.
Таким образом, разложение периодической функции в ряд Фурье эквивалентно представлению ее в виде бесконечной суммы гармоник, амплитуды которых  и фазы
и фазы 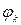 определяются коэффициентами Фурье
определяются коэффициентами Фурье 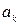 и
и 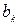 :
:
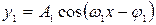 - первая гармоника,
- первая гармоника,
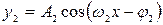 - вторая гармоника,
- вторая гармоника,
 - третья гармоника, … и так далее.
- третья гармоника, … и так далее.
Все гармоники имеют общий период  .
.
Разложение функции в тригонометрический ряд единственно.
Аппроксимирующие тригонометрические полиномы для функции  имеют вид:
имеют вид:
 ,
,
 ,
,
 ,
,
 ,
,
..................................
 .
.
Эти полиномы представляют собой частичные суммы ряда и являются последовательными приближениями функции  на
на  , с увеличением
, с увеличением 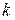 они все точнее и точнее представляют функцию
они все точнее и точнее представляют функцию  .
.
Периодическая функция 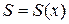 изображает периодическое движение (колебание) точки, имеющей в момент времени
изображает периодическое движение (колебание) точки, имеющей в момент времени 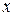 координату
координату 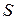 (на оси
(на оси 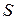 ).
).
Функция 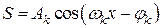 определяет гармоническое колебание точки с амплитудой
определяет гармоническое колебание точки с амплитудой  , фазой
, фазой 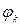 и частотой
и частотой  . Это функция периода
. Это функция периода 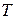 .
.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 1868; Нарушение авторских прав?; Мы поможем в написании вашей работы!