
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предельный признак сравнения числовых положительных рядов
|
|
|
|
Рассмотрим два положительных числовых ряда 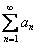 и
и  . Если предел отношения общих членов этих рядов равен конечному, отличному от нуля числу
. Если предел отношения общих членов этих рядов равен конечному, отличному от нуля числу 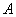 :
:  , то оба ряда сходятся или расходятся одновременно.
, то оба ряда сходятся или расходятся одновременно.
Когда применяется предельный признак сравнения? Предельный признак сравнения применяется тогда, когда «начинкой» ряда у нас являются многочлены. Либо один многочлен в знаменателе, либо многочлены и в числителе и в знаменателе. Один или оба многочлена также могут находиться под корнем.
Разделаемся с рядом, для которого не сработал предыдущий признак сравнения.
Пример 10
Исследовать ряд на сходимость 
Сравним данный ряд со сходящимся рядом  . Используем предельный признак сравнения. Известно, что ряд
. Используем предельный признак сравнения. Известно, что ряд  – сходится. Если нам удастся показать, что
– сходится. Если нам удастся показать, что 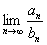 равен конечному, отличному от нуля числу, то будет доказано, что ряд
равен конечному, отличному от нуля числу, то будет доказано, что ряд 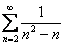 – тоже сходится.
– тоже сходится.

Получено конечное, отличное от нуля число, значит, исследуемый ряд сходится вместе с рядом  .
.
Почему для сравнения был выбран именно ряд  ? Если бы мы выбрали любой другой ряд из «обоймы» обобщенного гармонического ряда, то у нас не получилось бы в пределе конечного, отличного от нуля числа (можете поэкспериментировать).
? Если бы мы выбрали любой другой ряд из «обоймы» обобщенного гармонического ряда, то у нас не получилось бы в пределе конечного, отличного от нуля числа (можете поэкспериментировать).
Примечание: когда мы используем предельный признак сравнения, не имеет значения, в каком порядке составлять отношение общих членов, в рассмотренном примере отношение можно было составить наоборот:  – это не изменило бы сути дела.
– это не изменило бы сути дела.
Предельный признак сравнения применим почти для всех рядов, которые мы рассмотрели в предыдущем пункте:
 ,
,  ,
,  ,
,  .
.
Данные ряды по только что рассмотренной трафаретной схеме нужно предельно сравнить соответственно со сходящимися рядами:
 ,
, 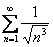 ,
, 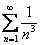 ,
,  .
.
Пример 11
Исследовать ряд на сходимость 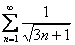
|
|
|
Это пример для самостоятельного решения.
Что делать, если многочлены находятся и в знаменателе, и в числителе? Алгоритм решения почти такой же – нам нужно подобрать для сравнения подходящий ряд из «обоймы» обобщенного гармонического ряда.
Пример 12
Исследовать ряд на сходимость 
Мы видим, что и в числителе и в знаменателе у нас многочлены, причем, в знаменателе многочлен находится под корнем. Подбираем ряд для сравнения  .
.
1) Сначала нужно найти старшую степень знаменателя. Если бы не было корня, то, понятно, что старшая степень знаменателя равнялась бы четырем. Что делать, когда есть корень? Об этом я уже рассказывал на уроке Методы решения пределов. Повторение – мать учения: мысленно или на черновике отбрасываем все члены, кроме старшего: 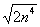 . Если есть константа, её тоже отбрасываем:
. Если есть константа, её тоже отбрасываем: 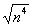 . Теперь извлекаем корень:
. Теперь извлекаем корень:  . Таким образом, старшая степень знаменателя равна двум.
. Таким образом, старшая степень знаменателя равна двум.
2) Выясняем старшую степень числителя. Очевидно, что она равна единице.
3) Из старшей степени знаменателя вычитаем старшую степень числителя: 2 – 1 = 1
Таким образом, наш ряд нужно сравнить с рядом  , то есть, с расходящимся гармоническим рядом.
, то есть, с расходящимся гармоническим рядом.
По мере накопления опыта решения эти три пункта можно и нужно проводить мысленно.
Само оформление решения должно выглядеть примерно так:
”
Сравним данный ряд с расходящимся гармоническим рядом 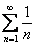 . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
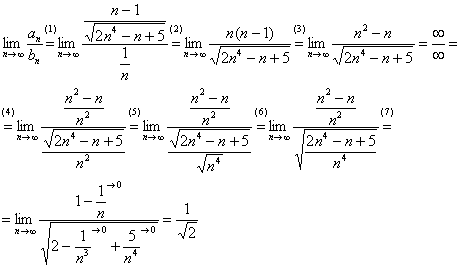
Получено конечное, отличное от нуля число, значит, исследуемый ряд расходится вместе с гармоническим рядом 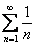 .
.
”
(1) Составляем отношение общих членов.
(2) Избавляемся от четырехэтажности дроби.
(3) Раскрываем в числителе скобки.
(4) Неопределенность  устраняем стандартным способом деления числителя и знаменателя на «эн» в старшей степени.
устраняем стандартным способом деления числителя и знаменателя на «эн» в старшей степени.
(5) В самой нижней строке подготавливаем  для внесения под корень:
для внесения под корень: 
(6) В знаменателе организуем общий корень.
Примечание: на практике пункты 5,6 можно пропустить, я их очень подробно разжевал для тех, кто не очень понимает, как обращаться с корнями.
(7) Почленно делим числители на знаменатели. Помечаем члены, которые стремятся к нулю.
|
|
|
Пример 13
Исследовать ряд на сходимость 
Это пример для самостоятельного решения.
В недалёком будущем вы будете сразу видеть, сходится такой ряд или расходится. Например, рассмотрим ряд 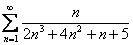 . Ага, 3 – 1 = 2, значит, ряд нужно сравнить со сходящимся рядом
. Ага, 3 – 1 = 2, значит, ряд нужно сравнить со сходящимся рядом  , и сразу можно сказать, что наш исследуемый ряд тоже сходится. Дело за малым – осталось аккуратно оформить стандартное рутинное решение.
, и сразу можно сказать, что наш исследуемый ряд тоже сходится. Дело за малым – осталось аккуратно оформить стандартное рутинное решение.
Вот, пожалуй, и все начальные сведения о положительных числовых рядах, которые потребуются вам при решении практических примеров. Следующий урок по теме числовых рядов – Признаки сходимости рядов. Признак Даламбера. Признаки Коши
Желаю успехов!
Решения и ответы:
Пример 2: 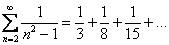
Примечание: обратите внимание, что переменная-«счётчик» в данном примере «заряжается» со значения 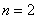
Пример 5: 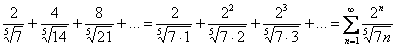
Пример 7:

Делим числитель и знаменатель на 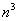

Исследуемый ряд расходится, так как не выполнен необходимый признак сходимости ряда.
Пример 9:
Сравним данный ряд с расходящимся гармоническим рядом 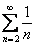 .
.
Используем признак сравнения:
Если 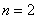 , то
, то 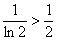
Если 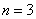 , то
, то 
Если 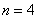 , то
, то 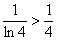
Таким образом, для всех членов ряда выполнено неравенство  , значит, по признаку сравнения исследуемый ряд расходится вместе с гармоническим рядом
, значит, по признаку сравнения исследуемый ряд расходится вместе с гармоническим рядом 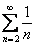 .
.
Примечание: И здесь есть неформальный смысл. Доказано, что гармонический ряд расходится, следовательно, сумма его членов:  . Мы показали, что члены ряда
. Мы показали, что члены ряда 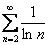 ещё больше членов ряда
ещё больше членов ряда 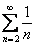 , и совершенно понятно, что сумма ряда
, и совершенно понятно, что сумма ряда 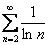 не может быть меньше бесконечности.
не может быть меньше бесконечности.
Пример 11:
Сравним данный ряд с расходящимся рядом  . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
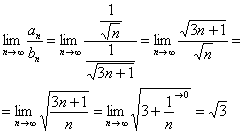
Получено конечное, отличное от нуля число, значит, исследуемый ряд расходится вместе с рядом  .
.
Пример 13:
Эти 3 пункта выполняем мысленно или на черновике:
1) Старшая степень знаменателя:4
2) Старшая степень числителя: 1
3) 4 – 1 = 3
Сравним данный ряд со сходящимся рядом 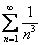 . Используем предельный признак сравнения:
. Используем предельный признак сравнения:

Получено конечное число, отличное от нуля, значит, исследуемый ряд сходится вместе с рядом 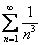 .
.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
|
|
|
(Переход на главную страницу)
Как можно отблагодарить автора?
Как найти сумму ряда?
Рассмотрим небольшую задачу, которая обычно предлагается в самом начале практической работы по теме. И такая привилегия не случайна. Для решения типового примера на нахождение суммы ряда не требуется тяжёлый багаж признаков сравнения, признаков Даламбера, Коши и т.д. – достаточно самых минимальных знаний о числовых рядах. Необходимо понимать, что такое ряд 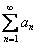 , уметь расписывать его подробно и не округлять глаза после словосочетаний «ряд сходится», «ряд расходится», «сумма ряда». Поэтому, если ваше настроение совсем на нуле, пожалуйста, уделите 5-10 минут статье Ряды для чайников (буквально первые 2-3 страницы), а потом возвращайтесь сюда и смело начинайте решать примеры!
, уметь расписывать его подробно и не округлять глаза после словосочетаний «ряд сходится», «ряд расходится», «сумма ряда». Поэтому, если ваше настроение совсем на нуле, пожалуйста, уделите 5-10 минут статье Ряды для чайников (буквально первые 2-3 страницы), а потом возвращайтесь сюда и смело начинайте решать примеры!
Следует отметить, что в большинстве случаев найти сумму ряда непросто, для этого часто используются солидные теоретические выкладки и специальные методы. Так, например, сумма популярного артиста  выводится через ряды Фурье. В этой связи на практике почти всегда требуется установить сам факт сходимости, но не найти конкретное число
выводится через ряды Фурье. В этой связи на практике почти всегда требуется установить сам факт сходимости, но не найти конкретное число 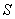 (многие, думаю, уже успели это заметить). Однако среди великого множества числовых рядов есть немногочисленные представители, которые позволяют без особых проблем прикоснуться к святая святых даже полному чайнику. И на вводном уроке я приводил пример бесконечно убывающей геометрической прогрессии
(многие, думаю, уже успели это заметить). Однако среди великого множества числовых рядов есть немногочисленные представители, которые позволяют без особых проблем прикоснуться к святая святых даже полному чайнику. И на вводном уроке я приводил пример бесконечно убывающей геометрической прогрессии  , сумма
, сумма 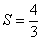 которой легко рассчитывается по известной школьной формуле.
которой легко рассчитывается по известной школьной формуле.
В данной статье мы продолжим рассматривать похожие примеры, кроме того, узнаем строгое определение суммы и попутно познакомимся с некоторыми свойствами рядов. Разомнёмся… да прямо на прогрессиях и разомнёмся:
Пример 1
Найти сумму ряда

Решение: представим наш ряд в виде суммы двух рядов:

Почему в данном случае так можно сделать? Выполненные действия основаны на двух простейших утверждениях:
1) Если сходятся ряды  , то будут сходиться и ряды, составленные из сумм или разностей соответствующих членов:
, то будут сходиться и ряды, составленные из сумм или разностей соответствующих членов: 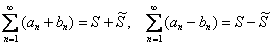 . При этом существенно то обстоятельство, что речь идёт о сходящихся рядах. В нашём примере мы заранее знаем, что обе геометрические прогрессии сойдутся, а значит, без всяких сомнений раскладываем исходный ряд в два ряда.
. При этом существенно то обстоятельство, что речь идёт о сходящихся рядах. В нашём примере мы заранее знаем, что обе геометрические прогрессии сойдутся, а значит, без всяких сомнений раскладываем исходный ряд в два ряда.
|
|
|
2) Второе свойство ещё очевиднее. Константу 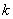 можно вынести за пределы ряда:
можно вынести за пределы ряда:  , причём это не повлияет на сходимость или расходимость ряда, а также на сумму ряда (если он сходится). Понятно, что множитель
, причём это не повлияет на сходимость или расходимость ряда, а также на сумму ряда (если он сходится). Понятно, что множитель 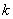 можно безболезненно внести и обратно.
можно безболезненно внести и обратно.
Чистовое оформление примера выглядит примерно так:
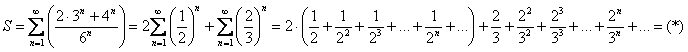
Дважды используем формулу для нахождения суммы бесконечно убывающей геометрической прогрессии: 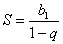 , где
, где 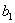 – первый член прогрессии,
– первый член прогрессии, 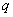 – основание прогрессии.
– основание прогрессии.

Ответ: сумма ряда 
Начало решения можно оформить несколько в другом стиле – расписать ряд напрямую и перегруппировать его члены:
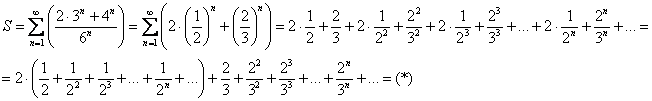
Дальше по накатанной.
Пример 2
Найти сумму ряда
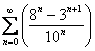
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Каких-либо особых изысков здесь нет, но однажды мне попался необычный ряд  , который может застать врасплох неискушенного человека. Это… тоже бесконечно убывающая геометрическая прогрессия! Действительно,
, который может застать врасплох неискушенного человека. Это… тоже бесконечно убывающая геометрическая прогрессия! Действительно,  , и сумма рассчитывается буквально за пару мгновений:
, и сумма рассчитывается буквально за пару мгновений:  .
.
А сейчас живительный глоток математического анализа, необходимый для решения дальнейших задач:
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 6409; Нарушение авторских прав?; Мы поможем в написании вашей работы!