Корректирующие коды

Корректирующими называются коды позволяющие обнаруживать и исправлять ошибки. Идею представления корректирующих кодов можно представить с помощью N-мерного куба. Возьмем трехмерный куб (рис.5.3), длина ребер, в котором равна одной единице. Вершины такого куба отображают двоичные коды. Минимальное расстояние между вершинами определяется минимальным количеством ребер, находящихся между вершинами. Это расстояние называется кодовым (или хэмминговым) и обозначается буквой d.

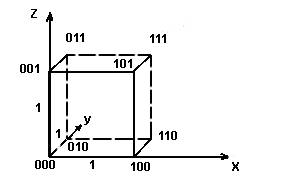
Рис.5.3. Представление двоичных кодов с помощью куба

Иначе, кодовое расстояние - это то минимальное число элементов, в которых одна кодовая комбинация отличается от другой. Для определения кодового расстояния достаточно сравнить две кодовые комбинации по модулю 2. Так, сложив две комбинации

11001010101

определим, что расстояние между ними d=7.

Для кода с N=3 восемь кодовых комбинаций размещаются на вершинах трехмерного куба. Такой код имеет кодовое расстояние d=1, и для передачи используются все восемь кодовых комбинаций 000,001,..,111. Такой код является не помехоустойчивым, он не в состоянии обнаружить ошибку.

Если выберем комбинации с кодовым расстоянием d=2, например, 000,110,101,011, то такой код позволит обнаруживать однократные ошибки. Назовем эти комбинации разрешенными, предназначенными для передачи информации. Все остальные 001,010,100,111 - запрещенные.

Любая одиночная ошибка приводит к тому, что разрешенная комбинация переходит в ближайшую, запрещенную комбинацию (см. рис.5.3). Получив запрещенную комбинацию, мы обнаружим ошибку. Выберем далее вершины с кодовым расстоянием d=3

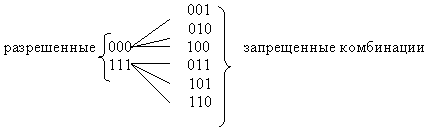
Такой код может исправить одну одиночную ошибку или обнаружить две ошибки. Таким образом, увеличивая кодовое расстояние можно увеличить помехоустойчивость кода. В общем случае кодовое расстояние определяется по формуле d=t + l + 1 где t - число исправляемых ошибок, l - число обнаруживаемых ошибок. Обычно l>t.

Большинство корректирующих кодов являются линейными кодами. Линейные коды - это такие коды, у которых контрольные символы образуются путем линейной комбинации информационных символов. Кроме того, корректирующие коды являются групповыми кодами. Групповые коды (G_n) - это такие коды, которые имеют одну основную операцию. При этом, должно соблюдаться условие замкнутости (то есть, при сложении двух элементов группы получается элемент принадлежащий этой же группе). Число разрядов в группе не должно увеличиваться. Этому условию удовлетворяет операция поразрядного сложения по модулю 2. В группе, кроме того, должен быть нулевой элемент.

Пример 5.3. Ниже приведены кодовые комбинации, являющиеся группой или нет.

1) 1101 1110 0111 1011 – не группа, так как нет нулевого элемента

2) 0000 1101 1110 0111 – не группа, так как не соблюдается условие замкнутости (1101+1110=0011)

3) 000 001 010 011 100 101 110 111 - группа

4) 000 001 010 111 - подгруппа

Большинство корректирующих кодов образуются путем добавления к исходной k - комбинации r - контрольных символов. В итоге в линию передаются n=k+r символов. При этом корректирующие коды называются (n,k) кодами. Как можно определить необходимое число контрольных символов?

Для построения кода способного обнаруживать и исправлять одиночную ошибку необходимое число контрольных разрядов будет составлять

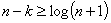. Это равносильно известной задаче о минимуме числа контрольных вопросов, на которые могут быть даны ответы вида “да” или “нет”, для однозначного определения одного из элементов конечного множества.

Если необходимо исправить две ошибки, то число различных исходов будет составлять Тогда , в этом случае обнаруживаются однократные и двукратные ошибки. В общем случае, число контрольных символов должно быть не меньше

(5.1)

Эта формула называется неравенством Хэмминга, или нижней границей Хэмминга для числа контрольных символов.

Дата добавления: 2015-07-02