О корнях полиномов и минимальных полиномах

Минимальным полиномом или функцией минимума элемента 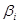поля GF(p^m) называется полином m_i(x) наименьшей степени с коэффициентами из GF(p), для которого 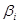является корнем, иначе говоря, m_i (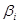)=0.

Рассмотрим теорему, которая является ключевой для построения порождающего полинома кода по последовательности корней, ее доказательство можно найти в книгах [1] и [2].

Теорема. 1. Предположим, что f_i(x) над GF(p) является минимальным полиномом элемента из GF(p^m). Тогда f(x) является также минимальным полиномом элемента .

Определение. Два элемента из GF(p^m) называются сопряженными, если они являются корнями одного и того же минимального полинома над GF(p) (это означает, что коэффициенты полинома лежат в GF(p)).

Следствие 1 теоремы 1:

Можно сделать вывод, что у элемента может быть не один сопряженный элемент, таких элементов может быть m или меньше. Используя теорему 1 можно составить последовательность сопряженных элементов, такую последовательность в литературе еще называют циклотомическим классом. Множество элементов, входящие в циклотомический класс (сопряженные элементы) можно найти по следующей формуле:

(1)

Где, С – циклотомический класс, s – степень элемента для которого находятся сопряженные элементы, p – показатель основного поля, m – число элементов расширения поля.

Рассмотрим пример нахождения циклотомического класса для элемента 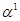из GF(2⁴). Здесь и далее будем представлять элемент, как его степень.

Итак, s = 1, p = 2, m = 4.

Таким образом, для элемента 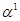будут сопряженными элементы

Следует иметь ввиду, что при построении циклотомического класса, степень элемента может быть выше максимальной степени, полученной при построении расширения поля, в этом случае необходимо разделить этот элемент на полином, по которому было построено расширение поля и взять остаток от деления (так как группа является циклической, см. выше). Также нужно иметь ввиду, что при построении циклотомического класса, некоторые элементы могут оказаться одинаковыми, тогда такой элемент присутствует в классе в одном экземпляре.

Следствие 2 из теоремы 1:

Два сопряженных между собой элемента будут иметь один и тот же минимальный полином.

Теорема 2. Минимальный полином элемента равен

,

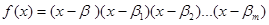где сопряженные элементы

Следствие из теоремы 2: Все элементы GF(p^m) являются корнями полиномов.

Построим минимальный полином для элемента 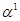из GF(2⁴). Сопряженные элементы для 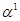найдены выше.

Используя теорему 2, запишем минимальный полином в общем виде:

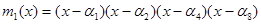
Теперь нужно раскрыть скобки, по обычным правилам, не приводя подобные, помня что, операция вычитания определена по правилам для поля GF(2), и она эквивалента операции сложения.

Если один из элементов имеет степень выше, чем максимальная степень элементов в таблице 1 (циклической группе), обозначим такой элемент как , то необходимо разделить на полином, по которому было построено расширение, и взять остаток от деления, остаток будет являться искомым элементом. Это обеспечивается тем, что мультипликативная группа примитивного элемента образует циклическую группу (см. выше).

Теперь, нужно заменить элементы разложения на элементы из GF(p^m), с учетом вышесказанного, раскрыть скобки, привести подобные, не забывая, что операция сложения проводится по модулю p (в данном примере по модулю два, так как в качестве основного поля выбрано GF(2)).

Резюме: Для нахождения минимального полинома для элемента из GF(p^m) необходимо:

1. Построить расширение поля по модулю некоторого неприводимого над GF(p) полинома.

2. Построить циклотомический класс для элемента , учитывая то, что одинаковые элементы в классе учитываются только один раз и то, что степень элемента класса может превышать максимальную степень элементов расширения поля.

3. При помощи теоремы 2 записать разложение минимального полинома, используя в качестве корней элементы циклотомического класса.

4. Раскрыть скобки разложения, не приводя подобные.

5. Проверить, не превышает ли степень максимальную степень элементов GF(p^m) (см. выше).

6. Заменить элементы на элементы поля.

7. Раскрыть скобки, привести подобные, учитывая тот факт, что суммирование ведется по модулю p.

Рассмотрим подробнее следствие 2 из теоремы 1:

Циклотомический класс для элемента 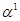: {1, 2, 4,8} для этих четырех элементов будут одинаковые минимальные полиномы.

Рассмотрим более подробно пример нахождения минимальных полиномов для GF(2⁴).

Построение GF(2⁴) рассмотрено выше, будем пользоваться готовым результатом.

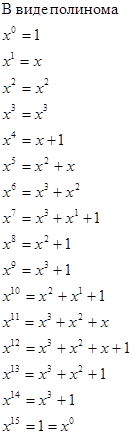
Таблица 2. Представление GF(2⁴).

Начнем с элемента 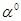. Исходя из формулы 1, запишем множество сопряженных элементов:

Так как все элементы получились одинаковыми, то циклотомический класс будет состоять из одного элемента – {0}.

При помощи теоремы 2 запишем: m₀(a⁰) = (x - a⁰), заменим a⁰ на элемент поля.

Минимальная функция для элемента a⁰: m₀(a⁰) = (x + 1)

Элемент .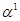

Используя формулу 1, получим циклотомический класс. {1, 2, 4, 8}.

Используя теорему 2, запишем разложение минимального полинома.

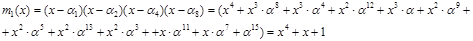
Теперь заменим a на элементы поля, после раскрытия скобок и приведения подобных получим минимальный полином для элементов со степенями 1, 2, 4, 8.

Элемент .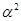

Исходя из теоремы 1 и следствия из нее, для элемента 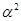минимальный полином будет равен полиному для элемента .

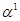Элемент .

Используя формулу 1, запишем циклотомический класс: C = {3,6,12,24}, как видно элемент со степенью 24 отсутствует в представлении поля GF(2⁴). Если разделить на полином, по модулю которого производилось построение GF(2⁴), то получим остаток .

Используя теорему 2, запишем разложение минимального полинома:

m₃(x) = (x – a³) (x – a⁶) (x – a⁹) (x – a¹²).

Теперь, раскрыв скобки и приведя подобные, получим полином m₃(x) = x⁴ + x³+ x² + x¹+1.

Следовательно, это полином для элементов со степенями 3,6,12,9.

Элемент .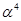

Минимальный полином этого элемента равен полиному элемента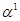

Элемент .

Используя формулу 1, запишем циклотомический класс: C = {5,10,5,10}. Так как элементы класса совпали, то в классе останется два элемента C = {5,10}.

Используя теорему 2, запишем разложение минимального полинома:

m₅(x) = (x – a⁵) (x – a¹⁰) = x² + x+1

Элемент .

Минимальный полином этого элемента равен полиному элемента

Элемент .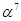

Используя формулу 1, запишем циклотомический класс: C = {7,14,28,56}. Так как , то C = {7,14,11,13}

Используя теорему 2, запишем разложение минимального полинома:

m₇(x) = (x – a⁷) (x – a¹⁴) (x – a¹¹) (x – a¹³) = x⁴ + x³+1

Нетрудно убедиться, что для остальных элементов минимальные полиномы уже найдены выше.

Дата добавления: 2015-07-02