Шаг 4. Нахождение порождающего полинома

Шаг 3. Нахождение минимальных полиномов.

Исходя из теоремы 2, для каждого корня найдем его минимальный полином, подробно нахождение минимальных полиномов описано выше.

Для корня со степенью 1:

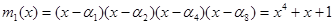
Для корня со степенью 3: m₃(x) = (x – a³) (x – a⁶) (x – a⁹) (x – a¹²) = x⁴ + x³+ x² + x¹+1.

Для корня со степенью 5: m₅(x) = (x – a⁵) (x – a¹⁰) = x² + x+1

Из 1.5 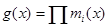, где 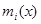это минимальные полиномы для заданных корней, то было получено, что

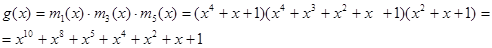
Заключение

В данной работе рассмотрено краткое математической описание циклических кодов с точки зрения алгебры конечных полей, которого вполне достаточно для решения задачи нахождения порождающего полинома кода, используя его корни. Безусловно, материал изложен в очень сжатой форме и многое нужно принять, как аксиому. Изначально данная работа задумывалась, как описание алгоритма нахождения полинома с некоторыми комментариями к каждому шагу, но в процессе описания алгоритма, оказалось, что без краткой теории конечных полей это сделать невозможно.

Список литературы

1. У. Питерсон, Э. Уэлдон. «Коды, исправляющие ошибки»: Москва: Мир, 1976.

2. Р. Блейхут. «Теория и практика кодов исправляющих ошибки»: Москва: Мир, 1986. - 576с.

3. Жуков А.Б., Каменский С.В. Передача сообщений. – НГТУ, 2003.

Приложения

Приложение А. Таблица неприводимых полиномов над GF(2).

Приложение Б. Таблица двоичных некоторых циклических кодов тривиальной длины

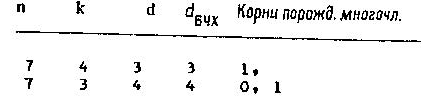
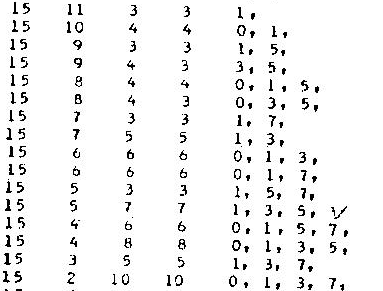
Дата добавления: 2015-07-02