Корректирующие коды. Статья 123.15. Казачье общество, внесенное в государственный реестр казачьих обществ в Российской Федерации

ВОПРОС № 15.

Статья 123.15. Казачье общество, внесенное в государственный реестр казачьих обществ в Российской Федерации

1. Казачьими обществами признаются внесенные в государственный реестр казачьих обществ в Российской Федерации объединения граждан, созданные в целях сохранения традиционных образа жизни, хозяйствования и культуры российского казачества, а также в иных целях, предусмотренных Федеральным законом от 5 декабря 2005 года N 154-ФЗ "О государственной службе российского казачества", добровольно принявших на себя в порядке, установленном законом, обязательства по несению государственной или иной службы.

2. Казачье общество по решению его членов может быть преобразовано в ассоциацию (союз) или автономную некоммерческую организацию.

3. Положения настоящего Кодекса о некоммерческих организациях применяются к казачьим обществам, внесенным в государственный реестр казачьих обществ в Российской Федерации, если иное не установлено Федеральным законом от 5 декабря 2005 года N 154-ФЗ "О государственной службе российского казачества".

ВОПРОС № 16.
Статья 123.16. Община коренных малочисленных народов Российской Федерации

1. Общинами коренных малочисленных народов Российской Федерации признаются добровольные объединения граждан, относящихся к коренным малочисленным народам Российской Федерации и объединившихся по кровнородственному и (или) территориально-соседскому признаку в целях защиты исконной среды обитания, сохранения и развития традиционных образа жизни, хозяйствования, промыслов и культуры.

2. Члены общины коренных малочисленных народов Российской Федерации имеют право на получение части ее имущества или компенсации стоимости такой части при выходе из общины или ее ликвидации в порядке, установленном законом.

3. Община коренных малочисленных народов Российской Федерации по решению ее членов может быть преобразована в ассоциацию (союз) или автономную некоммерческую организацию.

4. Положения настоящего Кодекса о некоммерческих организациях применяются к общинам коренных малочисленных народов Российской Федерации, если иное не установлено законом.

Корректирующими называются коды, которые позволяют обнаруживать ошибки и исправлять их на приемной стороне, не прибегая к повторной передаче ошибочных кодовых комбинаций.

Исходя из основных параметров и способов кодирования и декодирования, корректирующие коды в первую очередь можно разделить на блочные и непрерывные.

Блочные коды характеризуются тем, что каждая кодовая комбинация состоит из двух частей (блоков), первая состоит из информационных символов, вторая – из контрольных. Особенностью непрерывных кодов является то, кодовая комбинация не разделяется на блоки, а контрольные символы размещаются по определенному правилу между информационными.

Для корректирующих кодов справедливо неравенство

N = K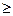^m M,

где М – количество сообщений; N – количество кодовых комбинаций; К – основание кода;

m – длина кодовой комбинации: m = n + k; n – число информационных разрядов, k – число контрольных разрядов, обеспечивающих локализацию и исправление искаженных элементов кодовой комбинации.

Число контрольных разрядов, необходимых для обнаружения и исправления однократных ошибок, определим путем следующих рассуждений. При передаче любого из М сообщений может быть искажен любой из m элементов кодовой комбинации или сообщение будет передано верно. Следовательно, возможны m + 1 исходов. Используя k контрольных разрядов необходимо различить все эти исходы. С помощью k разрядов можно закодировать 2k исходов. Значит, должно выполняться условие

Например, если М = 10, то в соответствии с равенством M = Kⁿ получаем n» 3,3 = 4. Чтобы иметь возможность обнаруживать ошибочные кодовые комбинации и исправлять их следует добавить k контрольных разрядов в соответствии с выражением:

При выполнении равенства получим . Таким образом, чтобы проверить четыре информационных разряда, требуется три контрольных.

При этом избыточность кода составит

.

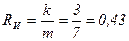Коды обнаруживающие ошибки должны иметь кодовое расстояние d = 2. Определим, чему должно равняться кодовое расстояние у корректирующих кодов. При этом поставим условие, что в одной кодовой комбинации не может возникнуть более одной ошибки. Выражение для определения кодового расстояния будет иметь вид:

,

где α – кратность обнаруживаемых ошибок,

β – кратность исправляемых ошибок,

1 – кодовое расстояние для оптимального кода;

Рассмотрим эту формулу на примере равномерного трехразрядного кода.

При α = 0, β = 0 d = 1. Этот результат соответствует равномерному оптимальному коду. Его кодовые комбинации: 000, 001, 010, 100, 110, 101, 011, 111.

При этом избыточность кода равна .

При α = 1, β = 0 d = 2. Этот результат соответствует равномерному коду, обнаруживающему однократную ошибку. Его кодовые комбинации: 001, 010, 101, 110.

При этом избыточность кода равна .

При α = 1, β = 1 d = 3. Этот результат соответствует равномерному оптимальному коду. Его кодовые комбинации: 000, 111.

При этом избыточность кода равна .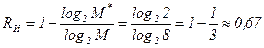

Общий алгоритм построения блочных кодов,

Дата добавления: 2015-07-02