
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы линейных алгебраических уравнений. Задачи для самостоятельной работы
|
|
|
|
Задачи для самостоятельной работы
ü Найдите матричное выражение АВT+3СT–2B. Докажите, выполнив умножение матриц, что (AB)C=A(BC). Докажите, выполнив умножение матриц и вычислив определители, что |AB|=|BA|=|A||B|.
1. 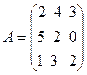 ,
, 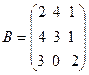 ,
,  .
.
2. 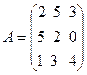 , B =
, B = 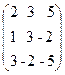 ,
, 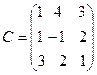 .
.
3. A =  , B =
, B = 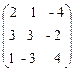 ,
, 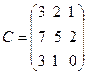 .
.
4. 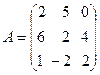 ,
, 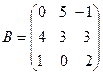 ,
, 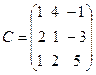 .
.
5. 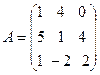 , B =
, B = 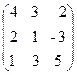 ,
, 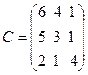 .
.
6. 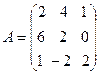 ,
, 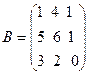 ,
, 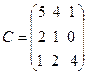 .
.
7. 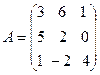 , B =
, B =  ,
,  .
.
8. A = 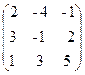 , B =
, B = 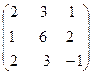 ,
,  .
.
9. 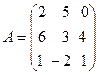 ,
, 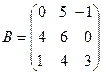 ,
, 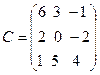 .
.
10.  . B =
. B = 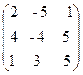 ,
,  .
.
11. 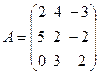 ,
, 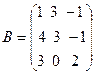 ,
, 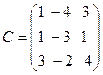 .
.
12. 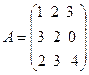 , B =
, B = 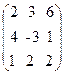 ,
, 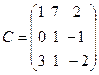 .
.
13. 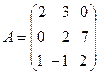 ,
, 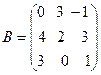 ,
,  .
.
14.  , B =
, B = 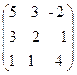 ,
, 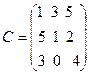 .
.
15. A= 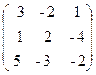 , B =
, B = 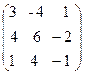 ,
,  .
.
16. 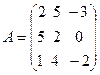 ,
, 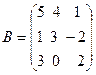 ,
, 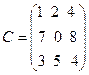 .
.
17. 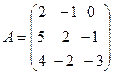 ,
, 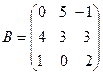 ,
, 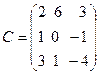 .
.
18.  , B =
, B = 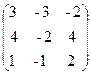 ,
, 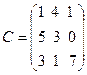 .
.
19.  , B =
, B = 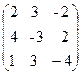 ,
,  .
.
20. 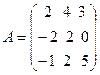 ,
,  ,
, 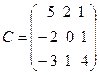 .
.
21. 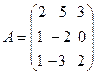 , B =
, B =  ,
,  .
.
22.  ,
, 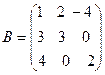 ,
, 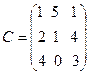 .
.
23. 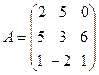 , B =
, B =  ,
, 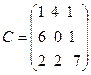 .
.
24. 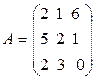 ,
, 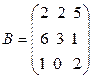 ,
,  .
.
25.  , B =
, B = 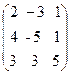 ,
, 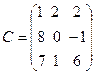 .
.
26. 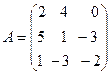 ,
,  ,
, 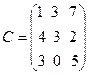 .
.
27. 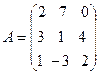 , B =
, B =  ,
, 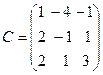 .
.
28. 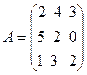 ,
, 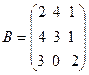 ,
, 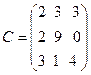 .
.
29. 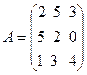 , B =
, B =  ,
, 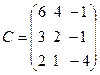 .
.
30. 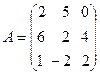 ,
, 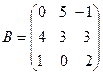 ,
, 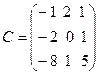 .
.
31. 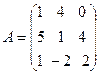 , B =
, B = 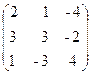 ,
, 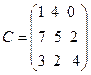 .
.
32.  ,
, 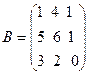 ,
, 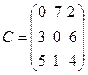 .
.
33. 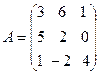 , A =
, A =  ,
, 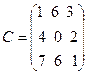 .
.
34. 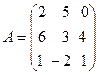 ,
, 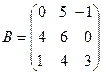 ,
,  .
.
35. 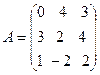 , B =
, B = 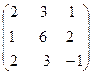 ,
,  .
.
36. A= 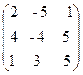 , B =
, B = 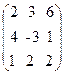 ,
, 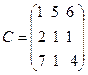 .
.
37. 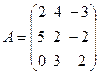 ,
, 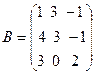 ,
, 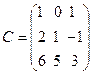 .
.
38. 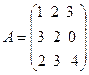 , B =
, B =  ,
, 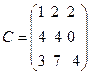 .
.
39. 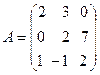 ,
, 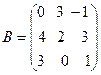 ,
,  .
.
40. A = 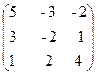 , B =
, B =  ,
, 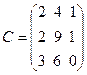 .
.
· Основные определения
Рассмотрим систему линейных алгебраических уравнений (СЛАУ):
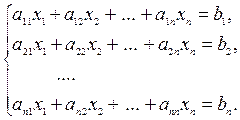
Матрицей системы называется матрица:
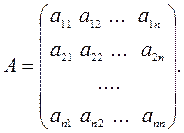
Столбцом свободных членов называется матрица-столбец:

Столбцом неизвестных называется матрица-столбец:
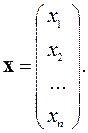
Тогда СЛАУ можно записать в матричном виде: 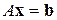 .
.
Расширенной матрицей системы называется матрица:
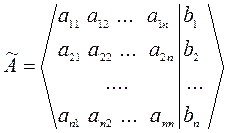 .
.
Существует три основных метода решения СЛАУ: Крамера, матричный и Гаусса.
· Метод Крамера
Метод Крамера применим, если определитель матрицы системы отличен от 0. Приведём формулы Крамера для СЛАУ третьего порядка


где
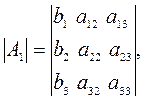
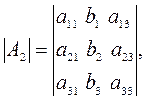
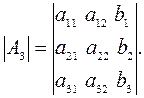
· Матричный метод
Матричный метод применим, если определитель матрицы системы отличен от 0.
Квадратная матрица  называется обратной матрицей для матрицы A, если
называется обратной матрицей для матрицы A, если 
Если матрица СЛАУ 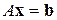 имеет обратную
имеет обратную  , то решение системы определяется по формуле:
, то решение системы определяется по формуле:  .
.
Пусть 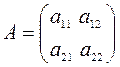 – квадратная матрица второго порядка, тогда обратная матрица имеет вид:
– квадратная матрица второго порядка, тогда обратная матрица имеет вид: 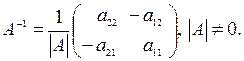
Пусть 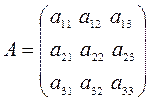 – квадратная матрица третьего порядка, тогда обратная матрица имеет вид:
– квадратная матрица третьего порядка, тогда обратная матрица имеет вид: 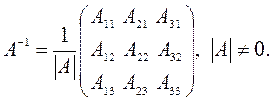
· Метод Гаусса
Метод Гаусса применим для любых СЛАУ и представляет собой последовательность эквивалентных преобразованиях расширенной матрицы системы.
|
|
|
Две расширенные матрицы системы называются эквивалентными, если соответствующие им СЛАУ равносильны.
Метод Гаусса использует три эквивалентных преобразования расширенных матриц, которые называются элементарными:
o перемена местами строк i и j (обозначение: 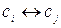 );
);
o умножение всех элементов строки i на ненулевое число  (обозначение:
(обозначение: 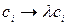 );
);
o прибавление ко всем элементам строки i соответствующих элементов строки j, умноженных на число  (обозначение:
(обозначение: 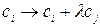 );
);
Суть метода Гаусса заключается в приведении матрицы системы с помощью элементарных преобразований к верхнетреугольной матрице (прямой ход), а затем к диагональной (обратный ход).
Пример 1.3. Решить систему уравнений Ax = b, методом Крамера, методом обратной матрицы и методом Гаусса, если A= 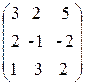 , x =
, x = 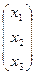 , b=
, b= 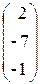 .
.
▼
· Решим систему методом Крамера.
1. 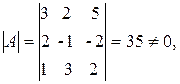 решение единственное.
решение единственное.
2. 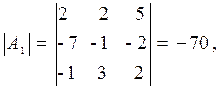

3. 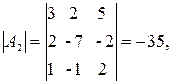
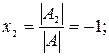
4.  ,
, 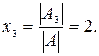
· Решим систему матричным методом.
1. 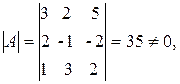 решение единственное.
решение единственное.
2. 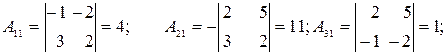
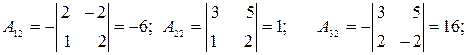
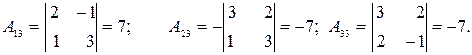
3. 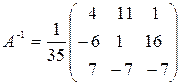 .
.
4. Из формулы  получаем:
получаем:
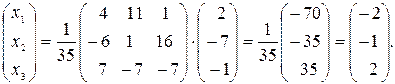
· Решим систему методом Гаусса.
1. Выпишем расширенную матрицу системы 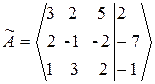 .
.
2. Прямой ход.
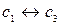
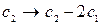
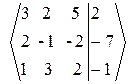 ~
~ 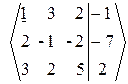 ~
~ 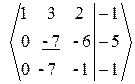 ~
~



~ 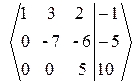 ~
~ 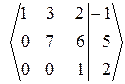
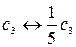
3.Обратный ход.
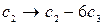
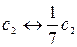
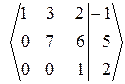 ~
~  ~
~ 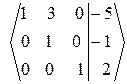 ~
~
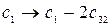
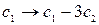
~ 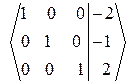 .
.
4.Ответ: 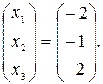
▲
Пример 1.4. Решить систему уравнений Ax = b методом Гаусса, если A= 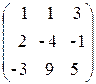 , x =
, x = 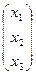 , b=
, b= 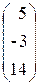 .
.
▼
1. Выпишем расширенную матрицу системы 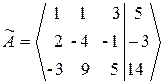 .
.
2. Прямой ход.
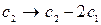
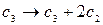
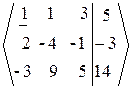 ~
~ 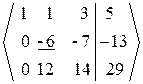 ~
~ 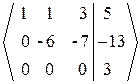
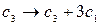
Последняя строка, полученной после элементарных преобразований расширенной матрицы, соответствует уравнению  , которое не имеет решений. Следовательно, система решений не имеет.
, которое не имеет решений. Следовательно, система решений не имеет.
▲
Пример 1.5. Решить систему уравнений Ax = b методом Гаусса, если A=  , x =
, x = 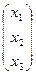 , b=
, b= 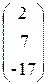 .
.
▼
1. Выпишем расширенную матрицу системы 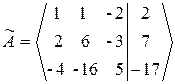 .
.
2. Прямой ход.
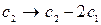
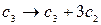
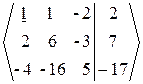 ~
~ 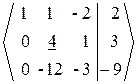 ~
~  .
.
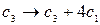
Нулевая строка может быть удалена из расширенной матрицы системы.
3. Обратный ход.
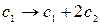
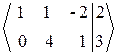 ~
~  .
.
Полученная после элементарных преобразований расширенная матрица, соответствует системе:
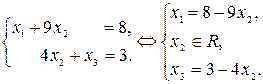
Следовательно, система имеет бесконечное множество решений.
|
|
|
▲
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 577; Нарушение авторских прав?; Мы поможем в написании вашей работы!