Устранение левой рекурсии и левая факторизация

Форме

Обобщенные КС-грамматики и приведение их к удлиняющей

КС-грамматика называется обобщенной, если она содержит аннулирующие правила ( e - правила ), то есть правила вида A ® e, где e - пустая цепочка. Обобщенная грамматика, зачастую, более проста и наглядна. Тем не менее следует помнить, что для любой обобщенной КС-грамматики существует эквивалентная неукорачивающая КС-грамматика.

Теорема 4.6. Каждая КС-грамматика приводима к виду с не более чем одним аннулирующим правилом S ® e, которого может и не быть.

Доказательство. Проведем его, как обычно, конструктивно, построением неукорачивающей грамматики.

Во первых, нужно определить, порождает ли исходная грамматика пустую цепочку. Пусть S - начальный символ исходной грамматики G. Определим в G множество нетерминалов X _i, из которых пустую цепочку можно получить за i шагов, и множество новых нетерминалов Z_i. Таким образом мы определим аннулирующие нетерминалы.

X₀ = { A | $ A® e }, Z₀ = X₀

X₁ = { A | $ A® x, где xÎ X₀ }, Z₁ = X₁\ X₀

....................................................................

X _i = { A | $ A® x, где xÎ X _j }, Z _i = X _i\ X _i-1

На каком-то шаге Z _i станет равным Æ и процесс формирования аннулирующих нетерминалов можно закончить. Если S Ï X _j, где , то e Ï L(G) и правила S® e добавлять не надо. В противном случае, заменим в исходной грамматике во всех правилах S на S₁, введем новый исходный нетерминал S и к правилам грамматики G добавим правила

S® e ½ S₁.

Все остальные правила вида A® e можно удалить. Для этого заменим каждое из правил, правые части которых содержат хотя бы по одному аннулирующему нетерминалу, множеством новых правил. Если правая часть правила содержит k вхождений аннулирующих нетерминалов, то множество, заменяющее это правило, будет состоять из 2^k правил, соответствующих всем возможным способам удаления некоторых (или всех) из этих вхождений.

Пусть имеется правило

B® j ₁ A ₁ j ₂ A ₂ j ₃ ... j _k A _k j _k+1,

где A _i () - аннулирующие нетерминалы. Добавим к этому правилу следующие правила:

B® j ₁ j ₂ A ₂ j ₃ ... j _k A _k j _k+1, удалено A ₁

B® j ₁ A ₁ j ₂ j ₃ ... j _k A _k j _k+1, удалено A ₂

..................................

B® j ₁ A ₁ j ₂ A ₂ j ₃ ... j _k j _k+1, удалено A _k

B® j ₁ j ₂ j ₃ ... j _k A _k j _k+1, удалены A ₁, A ₂

..................................

B® j ₁ j ₂ j ₃ ... j _k j _k+1, удалены A ₁, A ₂,... A _k

Заметим, что в случае неоднозначности, на этом шаге может получиться меньше чем 2^k правил. Так, для аннулирующего нетерминала A, правило B® aAA будет заменяться тремя правилами B® aAA ½ aA ½ a, так как в данном случае безразлично первое или второе вхождение A мы рассматриваем.

После такой замены правил, для всех правых частей исходной грамматики, содержащих аннулирующие нетерминалы, исключим из грамматики все e - правила, включая те, которые могли появиться при замене.

В результате мы получим грамматику, эквивалентную исходной, что доказывается с использованием теорем 4.1 и 4.3.

Отметим, что мы рассматривали случай, когда аннулирующие нетерминалы имеют и другие альтернативы, кроме перехода в пустую цепочку. Если A ® e единственная альтернатива нетерминала A, то правые части правил, содержащие его вхождение, можно просто исключить. ƒ

В результате применения рассмотренного алгоритма можно получить КС-грамматику, по которой вывод любой непустой цепочки характеризуется тем, что сентенциальная форма, получаемая на каждом шаге вывода, будет не короче предыдущей. Не случайно полученная грамматика носит название неукорачивающей КС-грамматики (НКС-грамматики).

Пример 4.5. Рассмотрим обобщенную КС-грамматику с аксиомой <число>

<число> ® <знак> <цел.часть>. <др.часть>

<знак> ® + ½ - ½ e

<цел.часть> ® <цел.часть><цифра> ½ e

<др.часть> ® <цел.часть>

<цифра> ® 0 ½ 1 ½...½ 8 ½ 9

и приведем ее к неукорачивающей форме. Вначале покажем, что данная грамматика не порождает пустой цепочки. Здесь

X₀ = { <знак>, <цел.часть> },

X₁ = { <др.часть> },

X₂ = Æ и Z₂ = Æ.

Среди множеств X - нет нетерминала <число> и, следовательно, правила

<число> ® e

добавлять не надо.

Проведем замены правил, правые части которых содержат аннулирующие нетерминалы, а затем удалим e - правила. В результате получим грамматику

<число> ® <знак> <цел.часть>. <др.часть> ½ <цел.часть>. <др.часть> ½

<знак>. <др.часть> ½ <знак> <цел.часть>. ½. <др.часть> ½

<цел.часть>. ½ <знак>. ½.

<цел.часть> ® <цел.часть><цифра> ½ <цифра>

<др.часть> ® <цел.часть>

<цифра> ® 0 ½ 1 ½...½ 8 ½ 9

На рис. 4.2 представлены деревья вывода цепочки +.9 по исходной (рис. 4.2 (а)) и результирующей (рис. 4.2 (б)) грамматикам.

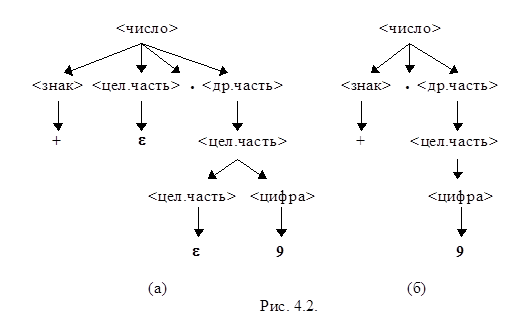š

Для приведения грамматики к удлиняющей форме необходимо кроме аннулирующих правил исключить и цепные правила. Цепное правило - это правило вида A ® B, где A, B Î N.

Теорема 4.7. Для любой КС-грамматики существует эквивалентная ей грамматика без цепных правил.

Доказательство. Пусть в грамматике имеется правило A ® B и A ¹ S (A - не начальный символ грамматики). Тогда все правила вида C ® aAb заменим на правила C ® aBb, а правила A ® B удалим. Если A = S и для B существуют правила B ® j ₁ ½ ... ½ j _n, то заменим их на S ® j ₁ ½ ... ½ j_n, после чего S ® B удалим.

Любое такое преобразование правил допустимо исходя из теорем 4.1 - 4.3 и устраняет правила вида A ® B. Повторяем такие преобразования до тех пор, пока в грамматике не останется цепных правил. š

В результате устранения аннулирующих и цепных правил получается грамматика в удлиняющей форме, где сентенциальная форма на каждом шаге вывода будет длиннее сентенциальной формы на предыдущем шаге. Напомним, что эта форма грамматики использовалась для доказательства теоремы о разрешимости контекстных языков (теорема 1.1).

Пример 4.6. Пусть дана КС-грамматика с правилами

S ® aBa

B ® A ½ Bc

A ® aA ½ bb.

Правило B ® A можно устранить, воспользовавшись результатами теоремы 4.2, и получить грамматику

S ® aBa

B ® aA ½ bb ½ Bc

A ® aA ½ bb š

КС-грамматика G=( N,S,P,S) называется грамматикой без циклов, если в ней нет выводов A Þ⁺ A для A Î N. КС-грамматика G называется приведенной, если она без циклов, без аннулирующих правил и без тупиков.

Грамматики с e - правилами и циклами иногда труднее анализировать, чем грамматики без таковых. Кроме того, в любой практической ситуации тупики (бесполезные символы) без необходимости увеличивают объем анализатора. Поэтому для некоторых алгоритмов синтаксического анализа, рассматриваемых во второй части пособия, мы будем требовать, чтобы грамматики, фигурирующие в них, были приведенными. Это требование позволяет рассматривать все КС-языки.

Теорема 4.8. Если L - КС-язык, то L=L(G) для некоторой приведенной КС-грамматики G.

Доказательство. Применить к КС-грамматике, определяющей язык L, эквивалентные преобразования по теоремам 4.5 - 4.7.?

В целом ряде приложений требуется, чтобы грамматика рассматриваемого языка не содержала левой рекурсии. Наличие леворекурсивных правил в исходной грамматике не фатально, так как для любой КС-грамматики существует эквивалентная грамматика без левой рекурсии.

Рассмотрим случай когда правила грамматики саморекурсивны, то есть левая часть правила и край правой части совпадают. Пусть нетерминал A имеет m леворекурсивных правил

A ® Aa _i для 1 £ i £ m

и n правил

A ® b _j для 1 £ j £ n,

которые не являются леворекурсивными (отметим, что отсутствие последних делает A тупиком). Заменив эти правила на правила

A ® b_j <список A> для 1 £ j £ n

<список A> ® a _i <список A> для 1 £ i £ m

<список A> ® e,

где <список A> - новый нетерминал, мы получим эквивалентную группу правил без левой рекурсии.

Пример 4.7. Самой короткой грамматикой для представления идентификатора является леворекурсивная грамматика

<И> ® б ½ <И>б ½ <И>ц,

где б - любая буква, а ц - любая цифра. В данной грамматике два леворекурсивных правила и одно правило без левой рекурсии. Заменяем их на правила

<И> ® б<И₁>

<И₁> ® б<И₁> ½ ц<И₁> ½ e,

мы получим обобщенную праворекурсивную грамматику идентификатора. Заметим, что исключение аннулирующего правила приведет нас к грамматике из примера 4.3. š

Если в грамматике имеется группа правил вида

A ® ab ₁ ½ ... ½ ab _n,

то цепочку a можно “вынести за скобку” и преобразовать данную группу правил к виду

A ® a B

B ® b ₁ ½ ... ½ b _n.

Этот прием носит название левой факторизации и его необходимо знать для ряда приложений.

Дата добавления: 2015-06-27