Графики расстояний точка-вершина для всех точек некоторого ребра

Абсолютные центры и абсолютные медианы

Пусть (r, s) – фиксированное ребро длины 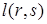, i – фиксированная вершина. Следовательно, известны числа 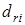и . Пусть f – переменная величина, .

Определение. Расстоянием точка-вершина (обозначение: 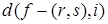) называется длина кратчайшего пути от данной f- точки на данной дуге (ребре) до данной вершины i.

Выведем формулу для расчета числа .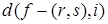

Случай 1. – дуга (рис. 7)

Если – дуга, путь из f- точки на дуге до вершины i состоит из двух частей: части дуги длины 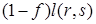и кратчайшего пути из вершины s до вершины i длины . Таким образом, (5)

Случай 2. – ребро (рис. 8).

Если – ребро, имеются две возможности пройти из f- точки ребра в вершину i: через вершину r или через вершину s. Длина первого пути равна сумме длина второго равна сумме Нужно выбрать путь меньшей длины. Значит, 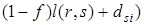(6)

Окончательно (7)

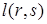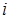Пусть – ребро графа G длины , – вершина графа G, . Построим график расстояния 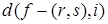как функции аргумента f.

В формуле (6) под знаком минимума стоят две линейные функции f: возрастающая (с положительным наклоном) – 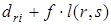и убывающая (с отрицательным наклоном) - 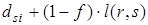= . Обозначим эти функции и соответственно.

Для каждого значения f, , выбирается 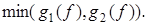Ввиду линейности функций g ₁и g ₂возможны только три варианта сочетания значений g ₁и g ₂.

Вариант 1.

(рис. 9).

График функции 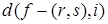показан на рис. 9 утолщенной линией.

Вариант 2.

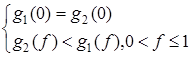(рис. 10).

График функции 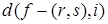показан на рис. 10 утолщенной линией.

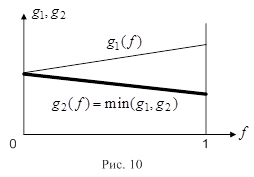
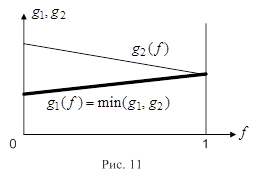
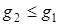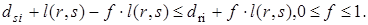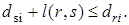Докажем, что если при , то . Пусть Положим . Тогда Но 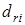– это длина кратчайшего пути от вершины r до вершины i, а – это длина пути от вершины r до вершины i, проходящего через ребро . Значит, Окончательно,

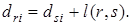
Вариант 3.

(рис. 11).

График расстояний 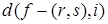показан на рис. 11 утолщенной линией.

Докажем, что если 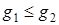при , то .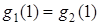

В самом деле, пусть 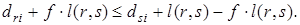Положим , тогда

Но – длина кратчайшего пути от вершины s до вершины i, a 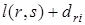– длина пути от вершины s до вершины i, проходящего через ребро . Поэтому 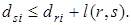Тогда .

Определение. Внешним абсолютным центром графа называется такая его точка, для которой минимально максимальное расстояние точка-вершина.

Ясно, что никакая внутренняя точка дуги не может быть абсолютным центром. Следовательно, абсолютным центром может быть либо вершина графа (тогда она является и центром), либо внутренняя точка одного из ребер графа.

Из сказанного следует такой алгоритм поиска абсолютного центра (алгоритм Хакими).

1. На каждом ребре данного графа отыскать точку с минимальным расстоянием точка-вершина.

2. Из всех таких найденных точек и центра выбрать абсолютно лучшую.

Найдем абсолютный внешний центр графа на рис. 1.

Построим графики расстояний точка-вершина для всех точек ребра (1,2) до всех вершин графа.

В силу линейности функций и достаточно сравнить их значения при и . Выпишем формулы и в двух строках и стрелкой укажем на меньшую из них. За стрелкой запишем, при каком значении f (0 или 1) меньше значение данной функции.

Итак, при функция меньше функции (В точке значения функций совпадают).

Далее

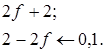
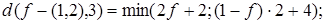
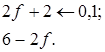
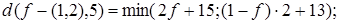
Построим пять этих графиков (рис. 12).

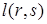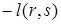Отметим, что на всех графиках как все прямые с положительным наклоном, так и все прямые с отрицательным наклоном параллельны, потому что в уравнениях этих прямых при переменной f стоит один и тот же коэффициент и соответственно.

Выделим утолщенными линиями верхнюю огибающую этих графиков.

В общем случае – это кусочно-линейная функция. Требуется выбрать точку (точки), в которых эта огибающая достигает абсолютного минимума. В данном случае абсолютного минимума она достигает в точке A (1; 13). Следовательно, минимум максимальных расстояний точка-вершина для точек ребра (1,2 ) равен 13 и достигается при f = 1, т. е. в вершине 2.

Построим соответствующие графики для точек ребра (2, 4) (рис. 13) для чего выполним необходимые расчеты.

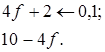
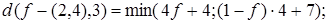
Сначала меньше значения функции ; потом становятся меньше значения функции . Найдем при котором начинается переход от функции к функции . В этой точке оба расстояния равны.

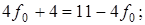
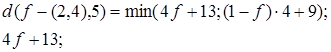
Минимум максимальных расстояний точка-вершина для точек ребра (2, 4) равен 9 и достигается при f= 1 (вершина 4 ).

Рассмотрим точки ребра (3, 4). Соответствующие графики построены на рис. 14. Имеем

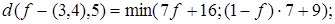
Минимум максимальных расстояний точка-вершина на ребре ( 3, 4 ) равен 9 и достигается в точке f=1 (вершина 4).

Рассмотрим точки ребра (4, 5) и определим расстояния

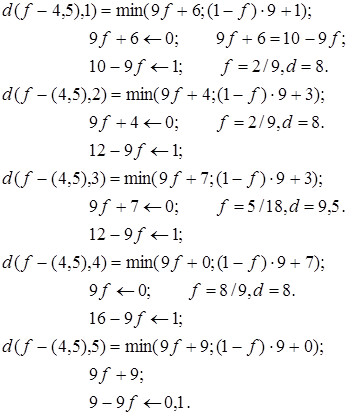
Графики расстояний точка-вершина приведены на рис. 15.

Минимум максимальных расстояний точка-вершина достигается в точке A (рис. 15). Найдем ее координаты. Точка A лежит на пересечении прямых и 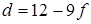. Отсюда и .

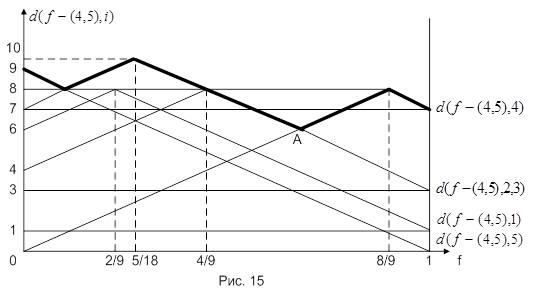Итак, минимум максимальных расстояний точка-вершина равен 6 и достигается при

Определим абсолютный внешний центр (табл. 4)

Абсолютным внешним центром этого графа является 2/3-точка ребра (4, 5); абсолютный минимум расстояний точка-вершина равен 6.

Таблица 4

Ребро
(1, 2)		1 (вершина 2)
(2, 4)		1 (вершина 4)
(3, 4)		1 (вершина 4)
(4, 5)		6/9
Внешний центр		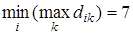Вершина 5

Определение. Абсолютной внешней медианой графа называется такая его точка, в которой минимизируется сумма расстояний точка-вершина.

Оказывается, что абсолютная медиана совпадает с медианой. Так получается потому, что любой график расстояний точка-вершина – это график выпуклой функции. Сумма выпуклых функций – это снова выпуклая функция. Минимум выпуклой функции на отрезке достигается в одном из концов отрезка.

Определение. Расстоянием вершина-точка (обозначение: ) называется длина кратчайшего пути от заданнойвершины 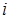до заданной 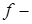точки на дуге (ребре) .

Формула для вычисления расстояния вершина-точка выводится подобно формуле для расстояния точка-вершина (рис. 16).

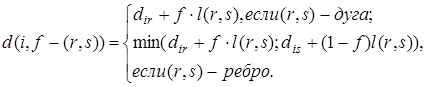(8)

Определение. Абсолютным внутренним центром называется такая точка графа, для которой минимально максимальное расстояние вершина-точка.

Поиск абсолютного внутреннего центра ничем не отличается от поиска абсолютного внешнего центра. Абсолютным внутренним центром может быть либо внутренняя точка некоторого ребра, либо первая вершина дуги (но тогда эта вершина одновременно – внутренний центр).

Найдем абсолютный внутренний центр графа на рис. 1.

Рассмотрим ребро (1, 2).

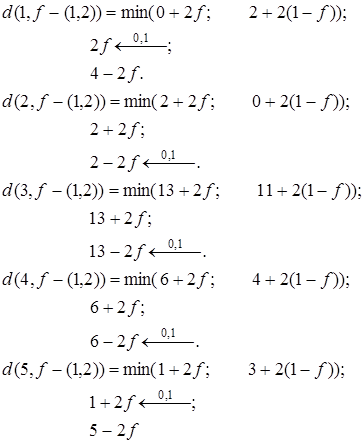
Соответствующие графики построены на рис. 17.

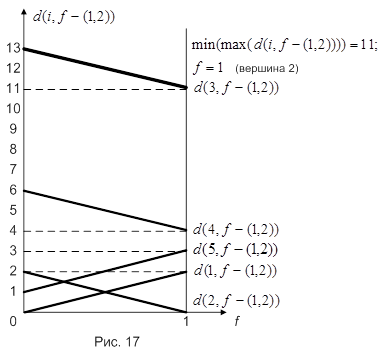
Рассмотрим ребро (2, 4) (рис. 18).

Рассмотрим ребро (3, 4) (рис. 19).

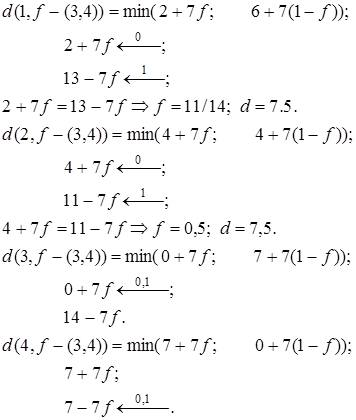
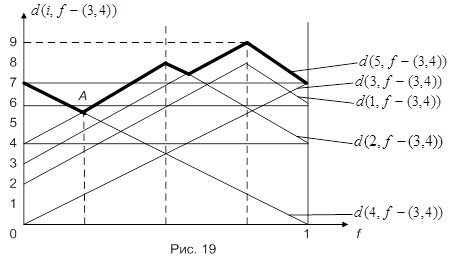
Минимум максимальных расстояний вершина-точка на рис. 19 достигается в точке A, лежащей на пересечении прямых и 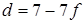, откуда и .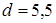

Перейдем к ребру (4, 5) (рис. 20).

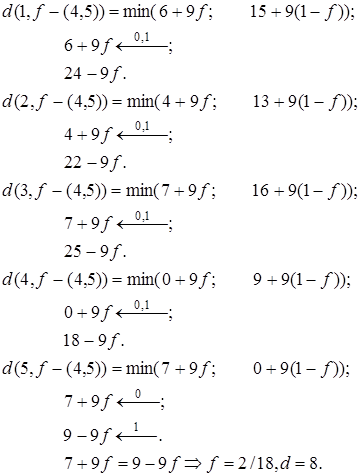
(вершина 4).

Таким образом (табл. 5), абсолютный внутренний центр этого графа - 3/14 точка ребра (3, 4). В ней достигается абсолютный минимум максимальных расстояний вершина-точка, равный 5,5.

Таблица 5

Ребро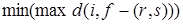
(1, 2)		1 (вершина 2)
(2, 4)		1 (вершина 4)
(3, 4)	5,5	3/14
(4, 5)		0 вершина 4
Внутренний центр		Вершины (3, 4)

Определение. Абсолютной внутренней медианой графа называется такая его точка, в которой минимизируется сумма расстояний вершина-точка. Абсолютная внутренняя медиана совпадает с внутренней медианой в силу тех же причин, по которым совпадают абсолютная внешняя и внешняя медианы.

Абсолютная внутренняя медиана данного графа – это вершина 3.

Дата добавления: 2015-07-02