Теорема 1.Если сходится,то сходится и . 2 страница

;

;

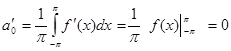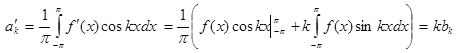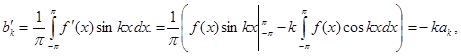Таким образом, ряд Фурье для производной 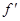записывается в следу- ющем виде: 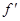(х) 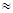. Легко заметить, что этот ряд можно получить, произведя формальное почленное дифференцирование ряда Фурье функции f. Этим обстоятельством пользуются, если известен ряд Фурье функции и требуется записать ряд Фурье производной этой функции. Обратим еще раз внимание на то, что при этом не нужно выяс- нять, разлагаются ли функция и её производная в ряды Фурье. Описанное построение ряда Фурье производной носит чисто формальный характер; сумма построенного ряда, если она вообще существует, вовсе не обяза- тельно совпадает с производной .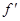

Теорема 1. (О почленном интегрировании ряда Фурье) Пусть функ- ция f непрерывна на и удовлетворяет условию f(-π) = f(π), а - её ряд Фурье. Тогда при всяком справед- ливо равенство

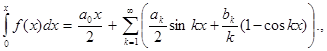причем ряд сходится равномерно на .

► Рассмотрим интеграл с переменным верхним пределом:

. Эта функция непрерывна на , причем 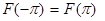, так как

=

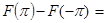
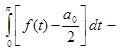
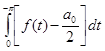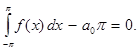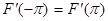= Функция F имеет на . непрерывную призводную: , причём, очевидно, . В силу теоремы 3 F разлагается на в равномерно сходящийся ряд Фурье:

.

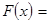
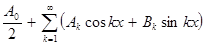Найдем коэффициенты этого ряда. При натуральных k, интегрируя по частям, получим:

=

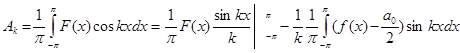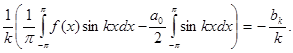= - Аналогично: 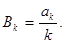Таким образом, при всяком х

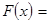
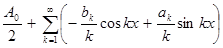. Положим здесь х = 0:

0 = 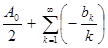. Отсюда: 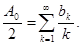Значит,

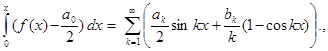
Отсюда: ◄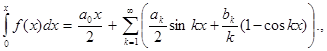

п.5. Ряды Фурье в случае произвольного промежутка

Пусть [ a,b ], a<b, - некоторый сегмент. Функция 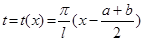, где , возрастает на [ a,b ] и отображает этот сегмент на . Об- ратная функция 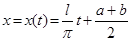возрастает на от a до b.

Пусть функция f (х) абсолютно интегрируема на [ a,b ]. Тогда функция определена на и абсолютно интегрируема на нем. Пусть ряд Фурье функции φ сходится на , а σ(t) – его сумма:

σ(t) = 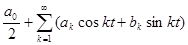. Обозначим: S (x) = σ( ). Функция S (x) есть сумма тригонометри- ческого ряда, сходящегнося на [ a,b ]:

S (x) = . Выразим коэфициенты 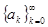и через функцию f:

;

при всяком натуральном k

;

.

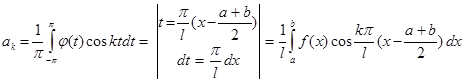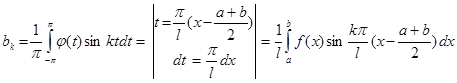Теоремы 1,2, и 3, п.3, описывают поведение суммы ряда Фурье σ(t) в зависимости от свойств функции 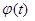. Используя замену 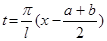, не- трудно получить из этих теорем аналогичные утверждения, описывающие поведение суммы S (x) в зависимости от свойств функции f (х). Например, из теоремы Дирихле следует: пусть функция f (х) кусочно- монотонна и кусочно- непрерывна на сегменте [ a,b ]; тогда

1) для всякого х (a,b) S (x) =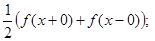

2)

Замечание. Во всякой точке интервала (a,b), в которой f непрерыв- на, имеет место равенство f(х) = S(x).

Отметим особо случай, когда сегмент [ a,b ] симметричен относи - тельно нуля: 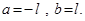Замена 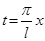отображает [- l,l ] на , обратная замена имеет вид Тогда тригонометрический ряд, построенный описанным выше способом для функции f(х), абсолютно интегрируемой на [- l,l ], будет выглядеть так: 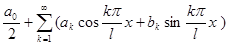, где 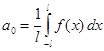, а при всяком натуральном k , .

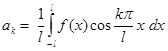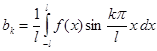Заметим ещё, что если f – чётная функция, то 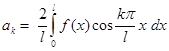, а , так что тригонометрический ряд содержит только косинусы: 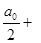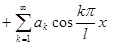. Если же f – нечётная функция,то 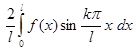а = , а 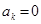, и ряд содержит только синусы: .

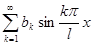п.6. Ряд Фурье функции с интегрируемым квадратом

Пусть функция f определена во всех точках сегмента , за исключением, быть может, точек x_j, j= 0,1,2,…,l, 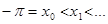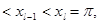и удовлетворяет требованию: интеграл 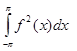существует. Такую функ- цию f будем называть функцией с интегрируемым на квадратом. Заметим, что функция с интегрируемым на квадратом, абсолютно интегрируема на . Действительно, из очевидного неравенства 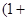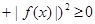следует: 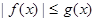, где , причем 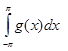существует; по признаку Вейерштрасса f абсолютно интегрируема на . Полеэно ещё заметить, что не всякая абсолютно интегрируемая функция имеет интегрируемый квадрат. Например, 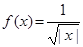: интеграл 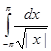сходится, а 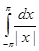- расходится.

Теорема 1. (Минимальное свойство коэффициентов Фурье)

Пусть f – функция с интегрируемым на квадратом, а

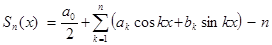- я частичная сумма ряда Фурье этой функции. Тогда для всякого тригонометрического многочлена 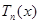порядка не выше n справедливо неравенство

.

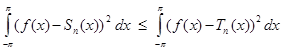► Рассмотрим 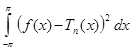, где T_n (x) 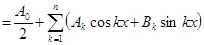. Имеем: 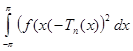= 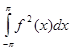-2 + .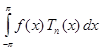

= =

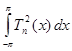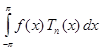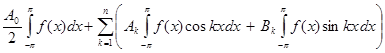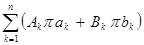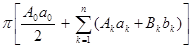= + = . Вычисляя 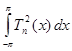, учитываем равенства леммы п.2:

= .

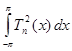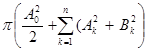Теперь получим:

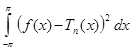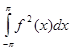= - 2 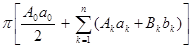+ + 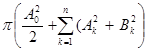= 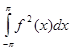+ 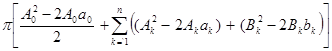. Каждую из разностей дополним до полного квадрата:

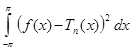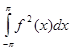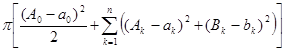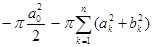
= + - . От коэффициентов многочлена 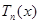зависит только выражение в квадрат- ных скобках; это выражение неотрицательно и обращается в нуль, когда коэффициенты многочлена совпадают с соответствующими коэффициен- тами Фурье функции f: 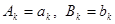, т.е. в случае 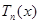= 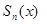. Значит, = . ◄

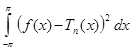
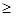
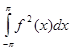
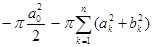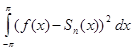Следствие. Если f – функция с интегрируемым на квадратом, то ряд 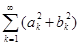сходится, причем справедливо неравенство (неравенство Бесселя) .

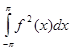► При всяком натуральном n имеем:

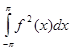
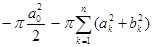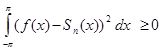= . Отсюда: всяком натуральном n 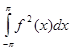. Перейдя здесь к пределу при , докажем и сходимость ряда 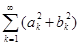, и неравенство Бесселя. ◄

На самом деле для всякой функции f, квадрат которой интегрируем на , справедливо равенство Парсеваля или уравнение замкнутости:

.

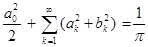
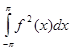Приведем доказательство этого равенства для функции, непрерыв- ной на .

► Зададим 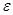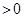. Так как f непрерывна на , по теореме Вей- ерштрасса (см. п.2) существует последовательность 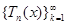тригономет- рических многочленов, равномерно сходящаяся на к f. Найдется натуральное число 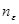такое, что для многочлена из указанной после- довательности на справедливо 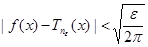. Для этого же многочлена имеем (см. доказательство теоремы):

.

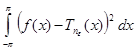
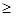
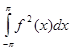
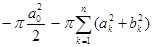
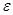
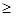
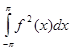
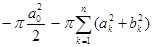
Таким образом, . Ввиду произ- вольности 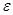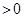отсюда вытекает равенство Парсеваля. ◄

Дата добавления: 2015-07-02