
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Собственные значения и собственные векторы подобных матриц
|
|
|
|
Если имеет место равенство  , то матрицы
, то матрицы  и
и 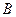 подобные (см. глава 6).
подобные (см. глава 6).
Докажем, что подобные матрицы имеют одинаковый спектр.
Теорема. Характеристические многочлены подобных матриц совпадают.
► Пусть матрицы  и
и 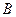 подобные. Тогда существует такая невырожденная матица
подобные. Тогда существует такая невырожденная матица  , что
, что  .
.
Покажем, что характеристические многочлены подобных матриц  и
и 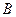 совпадают.
совпадают.
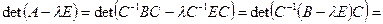

 .◄
.◄
Следствие 1. Характеристические уравнения подобных матриц совпадают  .
.
Следствие 2. Собственные значения подобных матриц совпадают.
Следствие 3. Для подобных матриц  и
и 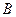
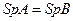 и
и  .
.
Замечание. Из равенств 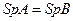 и
и  не всегда следует подобие матриц
не всегда следует подобие матриц  и
и 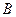 .
.
Например, матрицы 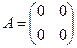 и
и 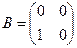 имеют одинаковые следы и одинаковые определители, но не являются подобными.
имеют одинаковые следы и одинаковые определители, но не являются подобными.
►Действительно, для любой невырожденной матрицы второго порядка  выражение
выражение 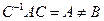 , откуда следует, что матрицы
, откуда следует, что матрицы  и
и 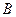 не являются подобными.◄
не являются подобными.◄
Теорема. Если  и
и  собственная пара матрицы
собственная пара матрицы  , то
, то  - собственная пара матрицы
- собственная пара матрицы 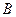 .
.
► Так как  собственная пара матрицы
собственная пара матрицы  , то
, то 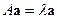 . Умножая
. Умножая 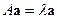 слева на
слева на  , имеем
, имеем 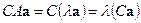 ,
,
с другой стороны,  , откуда
, откуда 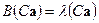 . Последнее означает, что
. Последнее означает, что  - собственная пара матрицы
- собственная пара матрицы 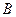 .◄
.◄
Замечание. Если  и матрица
и матрица  диагональная, то собственными значениями матрицы
диагональная, то собственными значениями матрицы  являются диагональные элементы
являются диагональные элементы  , а собственными векторами - единичные векторы
, а собственными векторами - единичные векторы 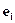 . Тогда в силу доказанной теоремы собственному значению
. Тогда в силу доказанной теоремы собственному значению 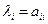 матрицы
матрицы 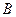 соответствует собственный вектор
соответствует собственный вектор  (
( -ый столбец матрицы
-ый столбец матрицы  ).
).
● Пример 9. Могут ли матрицы  =
=  и
и  быть подобными?
быть подобными?
Решение. Если матрицы подобны, то
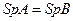
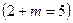 и
и 
 .
.
Система 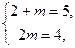 несовместна, откуда следует, что
несовместна, откуда следует, что
матрицы  и
и 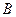 не могут быть подобными. ●
не могут быть подобными. ●
● Пример 10.Для любознательных. Доказать, что матрицы 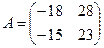 и
и  подобны.
подобны.
Решение.
Если матрицы  и
и 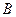 подобны, то существует хотя бы одна невырожденная матрица
подобны, то существует хотя бы одна невырожденная матрица  , что
, что  , и собственной паре
, и собственной паре 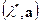 матрицы
матрицы  соответствует собственная пара
соответствует собственная пара  матрицы
матрицы 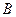 .
.
|
|
|
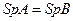 и
и  , откуда следует, что собственные значения матриц
, откуда следует, что собственные значения матриц  и
и 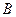 совпадают. Характеристическое уравнение матрицы
совпадают. Характеристическое уравнение матрицы  , а, следовательно, и матрицы
, а, следовательно, и матрицы 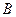 имеет вид
имеет вид 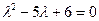 , корни которого
, корни которого 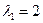 и
и  . Нетрудно проверить, что
. Нетрудно проверить, что  и
и 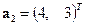 - собственные векторы матрицы
- собственные векторы матрицы  , соответствующие собственным значениям
, соответствующие собственным значениям 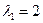 и
и  . Если существует такая матрица
. Если существует такая матрица  , что
, что  , то
, то  и
и 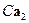 - собственные векторы матрицы
- собственные векторы матрицы 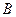 , соответствующие
, соответствующие 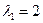 и
и  . Собственные векторы
. Собственные векторы  и
и 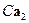 удовлетворяют системам
удовлетворяют системам  и
и  .
.
Пусть  . Тогда предыдущие уравнения могут быть записаны в виде
. Тогда предыдущие уравнения могут быть записаны в виде  ,
,  .
.
Первое матричное уравнение эквивалентно одному скалярному уравнению 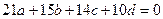 , второе - уравнению
, второе - уравнению  .
.
Для нахождения  ,
,  ,
,  и
и  имеем систему уравнений
имеем систему уравнений

ранг матрицы которой равен двум (минор второго порядка  ). Две неизвестные можно задать произвольно. Чтобы получить нетривиальное решение необходимо хотя бы одну неизвестную задать отличной от нуля.
). Две неизвестные можно задать произвольно. Чтобы получить нетривиальное решение необходимо хотя бы одну неизвестную задать отличной от нуля.
Пусть 
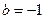 , тогда
, тогда 
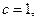
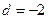 , матрица
, матрица  .
.
Следовательно, существует невырожденная матрица  такая, что
такая, что  и матрицы
и матрицы  и
и 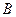 подобны. ●
подобны. ●
Замечание. Из произвольности выбора неизвестных следует, что можно подобрать бесконечное множество матриц  , таких, что
, таких, что  .
.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 3621; Нарушение авторских прав?; Мы поможем в написании вашей работы!