Однородные дифференциальные уравнения I порядка

def 1 ДУ вида

(1)

называется однородным дифференциальным уравнением I порядка (ОДУ).

Th 1 Пусть для функции выполнены условия:

1) непрерывна при

2)

Тогда ОДУ (1) имеет общий интеграл, который при задаётся формулой:

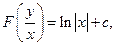(2)

где - некоторая первообразная функции 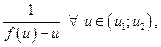с – произвольная константа.

Замечание 1 Если при некоторых 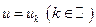будет выполнено условие 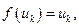то в процессе решения ОДУ (1) могут быть потеряны решения вида к таким случаям надо относиться внимательнее и проверять каждый из них отдельно.

Таким образом из теоремы Th1 следует общий алгоритм решения ОДУ (1):

1) Сделать замену:

(3);

2) Таким образом, будет получено ДУ с разделяющимися переменными, которое следует проинтегрировать;

3) Вернуться к старым gпеременным;

4) Проверить значения 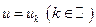, на их причастность к решению исходного ДУ, при которых будет выполнено условие

5) Записать ответ.

Пример 1 Решить ДУ 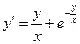(4).

Решение: ДУ (4) – это однородное дифференциальное уравнение, так как оно имеет вид (1). Сделаем замену (3), это приведёт уравнение (4) к виду:

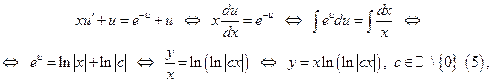
Уравнение (5) – это общий интеграл ДУ (4).

Заметим, что при разделении переменных и делении на могли быть потеряны решения, однако не является решением ДУ (4), что легко проверяется непосредственной подстановкой в равенство (4), так как это значение не входит в область определения исходного ДУ.

Ответ:

Замечание 2 Иногда встречается запись ОДУ через дифференциалы переменных х и у. Рекомендуется от этой записи ДУ перейти к выражению через производную и только затем выполнять замену (3).

Дифференциальные уравнения, приводящиеся к однородным.

def 2 Функцию называют однородной функцией степени k 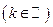в области , для которой будет выполнено равенство: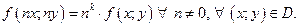

Вот наиболее часто встречающиеся типы ДУ, которые допускают приведение к виду (1) после различных преобразований.

1) где функция является однородной, степени нуль, то есть справедливо равенство: ДУ (6) легко приводится к виду (1), если положить , которое далее интегрируется с использованием замены (3).

2) 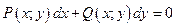(7), где функции являются однородными одной и той же степени k 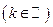. ДУ вида (7) также интегрируется с помощью замены (3).

Пример 2 Решить ДУ 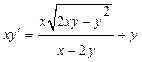(8).

Решение: Покажем, что ДУ (8) является однородным. Разделим на что возможно, так как не является решением ДУ (8).

(9),

Сделаем замену (3), это приведёт уравнение (9) к виду:

Уравнение (10) – это общий интеграл ДУ (8).

Заметим, что при разделении переменных и делении на 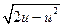могли быть потеряны решения, соответствующие значениям и . Проверим эти выражения. Подставим их в ДУ (8):

Ответ:

Интересно отметить, что при решении данного примера появляется функция называемая «знак» числа х (читается «сигнум икс»), определённая выражением:

Замечание 3 Приводить ДУ (6) или (7) к виду (1) не является обязательным, если очевидно, что ДУ является однородным, то можно и сразу произвести замену

3) ДУ вида (11), интегрируется как ОДУ если 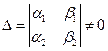, при этом первоначально выполняют подстановку:

(12), где 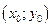- решение системы: (13), а затем используют замену (3) для функции После получения общего интеграла возвращаются к переменным х и у.

Если же 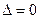, то, полагая в уравнении (11) получим ДУ с разделяющимися переменными.

Пример 3 Решить задачу Коши (14).

Решение: Покажем, что ДУ (14) приводится к однородному ДУ и интегрируется по вышеуказанной схеме:

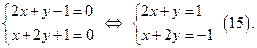
Решим неоднородную систему линейных алгебраических уравнений (15) методом Крамера:

Сделаем замену переменных и проинтегрируем полученное уравнение:

(16) – Общий интеграл ДУ (14). При разделении переменных могли быть потеряны решения при делении на выражение , которые могут быть получены в явном виде после решения квадратного уравнения 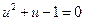. Однако, они учтены в общем интеграле (16) при

Найдём решение задачи Коши: подставим значения 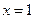и в общий интеграл (16) и найдём с.

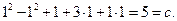
Таким образом, частный интеграл будет задаваться формулой:

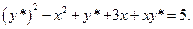
Ответ: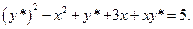

4) Некоторые ДУ возможно привести к однородным для новой, пока неизвестной функции , если применить замену вида:

. (17)

При этом число m подбирается из условия того, чтобы полученное уравнение, если это возможно, стало однородным какой-либо степени. Однако, если этого сделать нельзя, значит, рассматриваемое ДУ привести к однородному таким способом нельзя.

Пример 4 Решить ДУ . (18)

Решение: Покажем, что ДУ (18) приводится к однородному ДУ с помощью подстановки (17) и далее интегрируется с использованием замены (3):

ДУ (19) будет однородным только если показатели степеней всех его членов равны между собой, то есть:

Выполним подстановку:

(20)

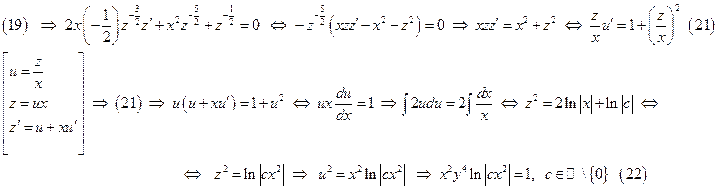
Уравнение (22) представляет собой общий интеграл ДУ (20). Однако, заметим, что при разделении переменных было потеряно решение исходного ДУ (20) , которое надо добавить в ответ. Также при использовании подстановки (20) было потеряно решение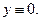

Ответ: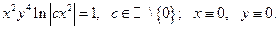

5) Рассмотрим так называемое обобщённое однородное ДУ.

def 3 ДУ вида 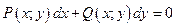называется обобщённым однородным, если удаётся подобрать такое число k, что левая часть этого уравнения становится однородной функцией некоторой степени m относительно х, у, dx и dy при условии, что х считается величиной первого измерения, у – k- го измерения, dx – нулевого измерения и dy– - го измерения.

Обобщённое однородное уравнение интегрируется при помощи подстановки:

Пример 5 Решить задачу Коши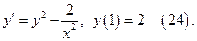

Решение: При сделанном выше предположении относительно измерений х, у, dx и dy, члены ДУ (24) будут иметь соответственно измерения 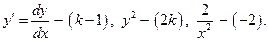Приравнивая эти величины, получаем условие, которому должно удовлетворять искомое число k:

Это условие выполняется при (при таком k все члены ДУ (24) будут иметь измерение(-2)). Следовательно, ДУ (24) является обобщённым однородным ДУ. Проинтегрируем его с помощью подстановки (23) при .

Найдём с:

Таким образом, частное решение ДУ (24) имеет вид

Ответ:

Дата добавления: 2015-06-27