Теоретическое обоснование методов хорд и касательных решения трансцендентных уравнений

Найдем координаты точки пересечения хорды, соединяющей концы дуги АВ кривой , с осью абсцисс ОХ ().

Угловой коэффициент хорды АВ равен 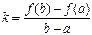, поэтому уравнение хорды можно записать так: .

В точке 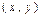пересечения хорды с осью ОХ ордината равна нулю, следовательно, (☺).

Аналогичным образом из уравнения можно получить формулу

(☺☺).

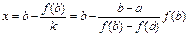Искомый корень уравнения должен находиться на отрезке, ординаты концов которого имеют разные знаки: .

Для доказательства сходимости процесса итерации предположим, что корень отделен, и вторая производная сохраняет постоянный знак на отрезке .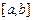

Пусть для определенности при . Тогда кривая вогнута и, следовательно, расположена ниже своей хорды АВ. Возможны два случая:

1) и 2) .

ξ

ξ

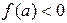Заметим, что 1) неподвижен тот конец, для которого знак функции совпадает со

знаком ее второй производной; 2) одна последовательность приближений монотонно убывает и ограничено снизу числом а, а другая – монотонно возрастает и ограничена сверху числом b, поэтому обе последовательности имеют предел, равный искомому корню x уравнения .

Для организации итерационного процесса решения уравнений методом хорд нужно выяснить, какой конец промежутка отделения корня неподвижен, и применить соответствующую формулу (☺) или (☺☺).

Найдя какое-нибудь приближение корня = x,, положим x = и по формуле Тейлора получим 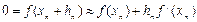. Откуда 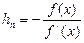. Таким образом, 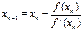– итерационная формула решения уравнений методом касательных.

Можно показать, что погрешность вычислений w оценивается так: 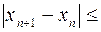w.

Литература

1. Араманович И.Г. Функции комплексного переменного. Операционное исчисление. Теория устойчивости / И.Г. Араманович, Г.А. Лунц, Л.Э. Эсгольц. – М.: Наука, 1968.

2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры – M: Наука, 1980, 1984. – 320с.

3. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. М.: Физматиздат, (1969 и позднее).

4. Берман Г.И. Сборник задач по курсу математического анализа. – М.: Физматиздат, издание стереотипное.

5. Боровков А.А. Математическая статистика. Оценка параметров. Проверка гипотез. – М.: Наука, 1984. – 472с.

6. Буколов Э.А., Ефимов А.В., Земсков В.Н. и др. Сборник задач по математике для втузов. Специальные курсы. / Под ред. А.В. Ефимова. – М.: Наука, 1984. – 606с.

7. Бутузов В.Ф., Крутицкая Н.И., Медведев Г.Н., Шишкин А.А. Математический анализ в вопросах и задачах. – М.: Высшая школа, 1993.

8. Вентцель Е.С. Теория вероятностей. – М.: Физматгиз,1962. – 564с.

9. Вентцель Е.С, Овчаров Л.А. Прикладные задачи теории вероятностей. – М.: Радио и связь, 1983. – 416с.

10. Волковыский Л.И. Сборник задач по теории функций комплексного переменного /Л.И. Волковыский, Г.А. Лунц, И.Г. Араманович. – М.: Наука, 1970.

11. Володин Б.Г., Ганин М.П., Динер И.Я. и др. Сборник задач по теории вероятностей, математической статистике и теории случайных функций / Под ред. А.А. Свешникова. – М.: Наука, 1970. – 656с.

12. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1977. – 480с.

13. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979. – 400с.

14. Гнеденко Б.В. Курс теории вероятностей. – М.: Наука,1988. – 448с.

15. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Т. 1. – М.: Высш. шк., 1970. – 416 с.

16. Задачи и упражнения по математическому анализу для втузов. /Под ред. Б.П. Демидовича. – М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2004. – 495с.

17. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1974. – 296с.

18. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч. 1. – М.: Наука, 1971.

19. Каплан И.А. Практические занятия по высшей математике. Ч. I, II, III, Ш, IV, V. Харьков: Издательство Харьковского государственного университета, 1971.

20. Кудрявцев Л.Д. Математический анализ. T.I, Т.2, Т3 – M.: Высш. школа, 1973.

21. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс. – М.: Рольф, 2001. – 576с.

22. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 2 курс. – М.: Айрис-пресс, 2004. – 592с.

23. Магазинников Л.И. Теория вероятностей. – Томск.: Изд-во Том. ун-та систем правления и радиоэлектроники, 2000. – 150 с.

24. Никольский С.М. Курс математического анализа. – М.: Наука, 1975.

25. Пантелеев А. В. Теория функций комплексного переменного и операционное исчисление в примерах и задачах /А. В. Пантелеев, А. С. Якимович. – М.: Высш. шк., 2001.

26. Пестова Н.Ф. Неопределенный интеграл. – Томск.: Изд-во Том. Политехнического ун-та, 1995. – 110 с.

27. Пискунов Н.С. Дифференциальное и интегральное исчисление. – М.: издание стереотипное (1960 г.и позднее).

28. Привалов И.И. Аналитическая геометрия. – М.: Наука, 1964. – 272с.

29. Пугачёв B.C. Теория вероятностей и математическая статистика. – М.: Наука, 1979. – 496с.

30. Радюк Л.Е., Терпугов А.Ф. Теория вероятностей и случайных процессов. – Томск.: Изд-во гос. ун-та, 1988. – 174с.

31. Румшиский Л.З. Элементы теории вероятностей. – М.: Наука, 1970. – 256с.

32. Севастьянов Б.А. Курс теории вероятностей и математической статистики. – М.: Наука, 1982. – 256с.

33. Тутубалин В.Н. Теория вероятностей. – М.: Изд-во МГУ, 1972. – 230с.

34. Феллер В. Введение в теорию вероятностей и её приложения. Т.1. – М.: Мир, 1964. – 498с.

35. Фукс Б.А. Функции комплексного переменного и некоторые их приложения /Б.А. Фукс, Б.В. Шабат. – М.: Наука, 1969.

36. Хапланов М.Г. Теория функций комплексного переменного/М. Г. Хапланов, – М.: Просвещение, 1965.

37. Хинчин А.Я. Краткий курс математического анализа, – М.: 1955.

38. Чистяков В.П. Курс теории вероятностей. – М.: Наука, 1982. – 256с.

39. Шилов Г.В. Математический анализ (функции одного переменного). Ч. 1-2. – М.: Наука, 1969.

40. Шипачев В.С. Высшая математика. – М.: Высш. шк., 1990. – 479 с.

41. Шнейдер В.Е. и др. Краткий курс высшей математики. Т. 1. – М.: Высш. шк., 1978. –384 с.

Дата добавления: 2015-06-27