
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теория двойственности
 |
Составление двойственной задачи. Пусть задача линейного программирования задана в стандартном виде:
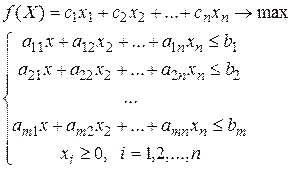 Û
Û 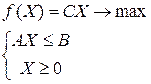 (4.1)
(4.1)
или
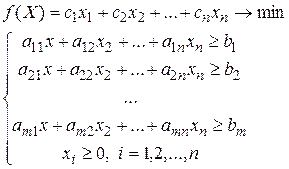 Û
Û 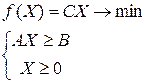 (4.2)
(4.2)
Двойственная задача составляется по следующим правилам:
- каждому ограничению (кроме условия неотрицательности переменных) ставится в соответствие переменная yi (i=1,2,…,m);
- матрицей коэффициентов системы ограничений двойственной задачи является транспонированная матрица исходной; вектор- столбец свободных членов исходной задачи становится вектор-строкой коэффициентов целевой функции;
- неравенства в системах ограничений имеют противоположный смысл;
- вектор-строка исходной целевой функции становится вектор-столбцом свободных членов в системе ограничений двойственной задачи;
- целевая функция двойственной задачи определяется противоположным по сравнению с целевой функции исходной задачи образом, т.е. если 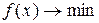 , то
, то 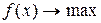 , и наоборот.
, и наоборот.
Таким образом, двойственная к (4.1) задача имеет вид
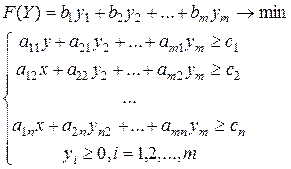 или
или 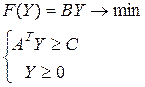
Двойственная к (4.2), соответственно:
 или
или 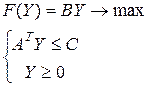
Замечание. Если в одной из задач ограничение, соответствующее новому переменному, представляет собой равенство, то с этого переменного снимается условие неотрицательности.
Пример. Записать задачу, двойственную к заданной:
а) 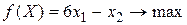
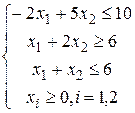
| б) 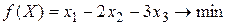
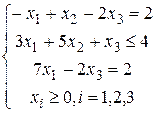
|
Решение. В случае а) все ограничения – неравенства. Приведем задачу к симметричному виду (функция стремится к максимуму, значит, все ограничения, кроме условия неотрицательности, должны иметь вид «£»). Чтобы этого добиться, поменяем знак во втором неравенстве. Затем введем новые переменные yi (i=1,2,3).
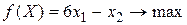
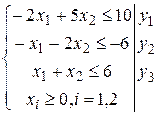
Учитывая правила построения двойственной задачи, получим:
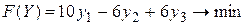
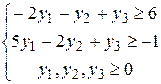
Для задачи б) меняем знак неравенства во втором ограничении, а также, после введения новых переменных, учитываем, что первое и третье ограничения – равенства, поэтому для соответствующих переменных требования неотрицательности не будет. Исходная задача принимает вид
|
|
|
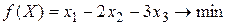
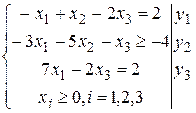 ,
,
а двойственная к ней –
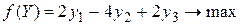
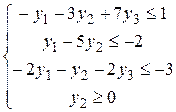
Первая теорема двойственности. Формулировка утверждения звучит следующим образом: если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем оптимальные значения целевых функций совпадают. Если одна из пары двойственных задач не имеет решения в силу неограниченности целевой функции, то вторая не имеет решения в силу несовместности системы ограничений.
При использовании этого утверждения симплекс-методом сначала находится оптимальное решение одной из задач, а затем – оптимальное решение второй задачи с помощью правила, которое выводится в ходе доказательства теоремы. В частности, если X* - оптимальное решение исходной задачи, то Y*=C*D-1, где C* - вектор-строка коэффициентов целевой функции, соответствующих базисным переменным оптимального решения, а D-1 –матрица, обратная к матрице D, составленной из столбцов матрицы ограничений исходной задачи (матрицы, с которой начиналась реализация симплекс-метода), соответствующих базисным переменным.
Пример 4.2. Записать задачу, двойственную к
 ,
,
решить исходную задачу симплекс-методом и выписать оптимальное решение двойственной задачи:
Решение. Оба ограничения заданы равенствами (нет требования неотрицательности новых переменных), поэтому двойственная задача имеет вид:
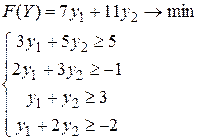
Исходная задача решена симплекс-методом в п.3.1: Xоптим=(2;0;1;0). Базисные переменные здесь x1, x3, поэтому C*=(5;3), 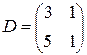 и легко проверить, что
и легко проверить, что 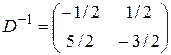 . Тогда
. Тогда 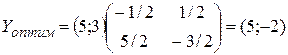 . При этом, как и следует из первой теоремы двойственности,
. При этом, как и следует из первой теоремы двойственности,
Fmin=F(5;-2)=13=fmax=f(2;0;1;0). (4.3)
Читателю предлагается проверить, что действительно найдено оптимальное решение двойственной задачи (например, графическим способом).
|
|
|
Вторая теорема двойственности. Один из способов совместного решения пары двойственных задач основан на следующем утверждении: если в оптимальном решении одной из двойственных задач одна из переменных отлична от нуля, то соответствующее ей ограничение второй задачи обращается в равенство; если оптимальное решение обращает ограничение одной из задач в строгое неравенство, то соответствующая переменная в оптимальном плане второй задачи равна нулю.
Рассмотрим пару двойственных задач, разобранную в примере 4.2. Предположим, что нам известно решение второй задачи, т.е. 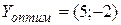 . Здесь оба значения переменных в оптимальном плане не равны нулю, значит, ограничения первой задачи должны выполняться как равенства. Теперь будем поочередно подставлять
. Здесь оба значения переменных в оптимальном плане не равны нулю, значит, ограничения первой задачи должны выполняться как равенства. Теперь будем поочередно подставлять 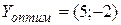 в ограничения второй задачи: 15-10=5; 10-6=4>-1; поэтому x2=0; 5-2=3; 5-4=-1>-2, поэтому x4=0. Учитывая, что x2=0 и x4=0, из ограничений-равенств первой задачи получаем систему уравнений:
в ограничения второй задачи: 15-10=5; 10-6=4>-1; поэтому x2=0; 5-2=3; 5-4=-1>-2, поэтому x4=0. Учитывая, что x2=0 и x4=0, из ограничений-равенств первой задачи получаем систему уравнений: 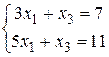 . Решив ее, например, методом исключения переменной, получаем: x1=2 и x3=1.
. Решив ее, например, методом исключения переменной, получаем: x1=2 и x3=1.
Таким образом, Xоптим=(2;0;1;0), причем, в силу первой теоремы двойственности, снова выполняется (4.3).
ТРАНСПОРТНАЯ ЗАДАЧА
1. Постановка задачи и математическая модель. Предположим, что существуют N потребителей и M поставщиков некоторого однородного груза, у каждого из поставщиков определенный запас этого груза (Ai единиц, i=1,2,…,M), а каждому из потребителей требуется Bj единиц груза (j=1,2,…, N). Известны также затраты cij на перевозку единицы груза от поставщика Ai к потребителю Bj. Требуется составить такой план перевозок от поставщиков к потребителям, чтобы суммарные затраты на перевозки оказались минимальными (при этом должны быть по возможности вывезены все запасы поставщиков и удовлетворены все запросы потребителей).
В случае, когда суммарные запасы совпадают с суммарными запросами, задача называется задачей с правильным балансом, а ее модель - закрытой. В противном случае говорят о задаче с неправильным балансом и об открытой модели. Существуют специальные приемы приведения открытой модели к закрытой (они будут рассмотрены позже).
Данные транспортной задачи обычно записываются в виде таблицы, заголовки строк которой содержат информацию о запасах, заголовки столбцов – информацию о запросах, а в нижнем правом углу каждой ячейки указывается стоимость перевозки единицы груза (затраты на перевозку единицы груза).
|
|
|
При составлении математической модели через xij обозначается количество единиц груза, который будет перевезен от поставщика Ai к потребителю Bj (объем перевозок от Ai к Bj). Эти значения будут вноситься в центр соответствующей ячейки.
С учетом сказанного целевая функция принимает вид
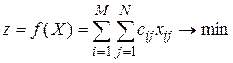
(просуммированы все произведения затрат на соответствующий объем перевозок). Ограничения связаны с вывозом запасов и удовлетворением запросов, поэтому математическая модель имеет вид:
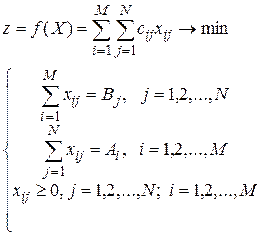
| Пример. Транспортная задача задана с помощью таблицы 5.1, из которой видно, что на складах трех поставщиков A1, A2, A3 сосредоточены соответственно 30, 190 и 250 единиц груза, потребители B1, B2, B3, B4 нуждаются соответственно в 70, 120, 150, 130 единицах груза, а стоимости перевозок указаны непосредственно в таблице. |
Таблица 5.1. |
Заметим, что суммарные запасы (30+190+250=470) равны суммарным запросам (70+120+150+130=470). Разместим в основной (незаштрихованной) части таблицы искомые объемы перевозок xij и перейдем к составлению математической модели. Заметим, что нумерация соответствует привычной нумерации элементов в матрицах (i – номер строки, j – номер столбца). Итак, целевая функция принимает вид
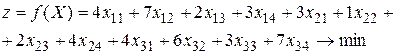 (5.1)
(5.1)
(просуммировали произведения стоимостей на объемы перевозок по всем строкам). При построении системы ограничений сначала суммируем объемы перевозок по каждому столбцу (удовлетворяем все запросы), а потом суммируем объемы перевозок по каждой строке (вывозим все запасы). Учтем также неотрицательность значений xij и получаем следующие условия:
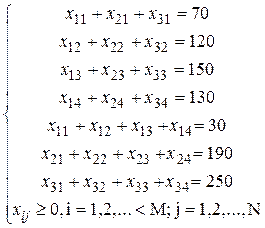 (5.2)
(5.2)
Итак, мы построили математическую модель предложенной задачи с целевой функцией (5.1) и системой ограничений (5.2).
Транспортная задача сводится к задаче линейного программирования, однако для ее решения существуют специальные алгоритмы. При этом сначала задача сводится к закрытой, затем строится начальное решение, а затем оно оптимизируется с помощью метода потенциалов. В связи с этим всюду далее алгоритмы излагаются в общем виде для закрытой задачи.
|
|
|
2. Построение начального опорного решения. Рассмотрим два основных приема для задач с правильным балансом. Первый из них имеет более простой алгоритм, а второй дает решение, более близкое к оптимальному.
Метод северо-западного угла. Основная идея заключается в том, вычисление значений xij начинается с верхней левой клетки (северо-западный угол таблицы). Из значений запасов и запросов, ей соответствующих (A1 и B1) выбираем минимальное – это и будет объем перевозок x11. При этом либо удовлетворены все запросы (и тогда из рассмотрения исключается потребитель, при этом в таблице в оставшихся ячейках соответствующего столбца ставятся прочерки, а объем запасов в соответствующей строке уменьшается на это значение), либо вывезены все запасы (из рассмотрения исключается поставщик, прочерки ставятся в строке и уменьшается объем запросов). В случае, когда A1 = B1, вычеркивается либо строка, либо столбец (но не строка и столбец одновременно! ) Далее действия повторяются со следующей ячейкой, которая оказалась верхней левой – и так до момента, пока не окажется, что все запасы вывезены, а все запросы удовлетворены. При этом клетки, в которые попали значения xij,, называются занятыми.
Внимание! Во избежание ошибок необходимо убедиться в том, что число занятых клеток равно M+N-1; в противном случае построенное начальное решение не будет опорным. При этом необходимо помнить, что, в силу сформулированного правила выбора объема перевозок, в занятых клетках могут оказаться значения, равные нулю!
Пример. Ниже в таблицах 5.2-5.7 приводится пошаговое построение методом северо-западного угла начального опорного решения для закрытой задачи из примера 5.1; объемы перевозок внесены в таблицы жирным курсивным шрифтом.
Таблица 5.2. |
Таблица 5.3. | ||||||||||||||||||||||||||||||||||||||||
Таблица 5.4. |
Таблица 5.5 |
Таблица 5.6. |
Таблица 5.7. |
Итак, заняты 6 ячеек: (1;1), (2;1), (2;2), (2;3), (3;3) и (3;4) (здесь, как и всюду далее, в «адресе» ячейки первым указан номер строки, вторым – номер столбца, заголовки в нумерации не учитываются). Количество занятых ячеек совпадает с числом M+N-1=3+4-1=6. Мы построили начальное опорное решение X1, остается найти значение целевой функции для этого опорного решения (в свободных клетках, т.е. клетках с прочерками, значение объема перевозок считается равным нулю и потому на результат вычисления не влияет): 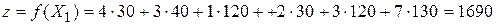 .
.
Метод минимальной стоимости. Основная идея этого подхода - последовательная расстановка объемов перевозок в клетки с наименьшей стоимостью среди незаполненных. В случае, когда есть несколько клеток с одинаковой стоимостью, первой рассматривается та, в которую можно записать наибольший объем перевозок. Правило выбора значения из соответствующих запаса и запроса сохраняется, как сохраняется и обязательное количество занятых строк, и возможность появления в занятой клетке нулевого значения.
Пример. В таблицах 5.8-5.13 приводится пошаговое построение начального опорного решения методом минимальной стоимости для закрытой задачи из примера 5.1. Обратите внимание, что первый выбор сделать легко, а в таблице 5.8 видно, что в ячейках (2;3) и (1;3) одинаковая стоимость затрат (равная 2). Поскольку в ячейку (2;3) можно записать объем перевозок, равный 70, а в ячейку (1;3) – равный 30, выбираем ячейку с бОльшим объемом, т.е. (2;3) – см. таблицу 5.9.
Таблица 5.8. |
Таблица 5.9. |
Таблица 5.10. |
Таблица 5.11 |
Таблица 5.12. |
Таблица 5.13 |
В итоге, как и положено, построенному начальному опорному решению X2 соответствуют 6 занятых клеток. При этом значение целевой функции 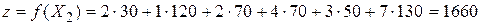 меньше, чем найденное в примере 5.2, т.е. решение X2 ближе к оптимальному.
меньше, чем найденное в примере 5.2, т.е. решение X2 ближе к оптимальному.
Открытую модель необходимо сначала свести к закрытой, для чего вводится фиктивный поставщик (с запасами, равными разности между запасами и запросами) или фиктивный потребитель (с аналогично определяемыми запросами). Стоимости перевозок в соответствующих строке или столбце равны нулю, но в методе минимальной стоимости они учитываются в последнюю очередь. В ответе фиктивная строка (столбец) не учитывается.
| Пример. Для предложенной транспортной задачи (таблица 5.14) составить начальные опорные решения методами северо-западного угла и минимальной стоимости и сравнить значения целевой функции. |
|
Решение. Прежде всего очевидно, что суммарные запасы равны 100, а суммарные запросы – 90. Поэтому необходимо ввести фиктивного потребителя, запросы которого равны 10 (это дополнительный столбец, значения стоимостей в котором будут равны 0) – см. таблицу 5.15, с которой начнем построение начального решения методом северо-западного угла. На первом шаге для ячейки (1;1) значения запасов и запросов одинаковы и равны 30, поэтому объема перевозок равен 30, вычеркиваем, например, строку (при этом запросы в соответствующем столбце становятся равными 0). На следующем шаге (см. таблицу 5.16) в ячейку (2;1) ставится значение объема перевозок 0 – как минимальное из чисел 0 и 20, при этом вычеркивается первый столбец.
Таблица 5.15. |
Таблица 5.16. | ||||||||||||||||||||||||||||||||
Таблица 5.17. |
Таблица 5.18. | ||||||||||||||||||||||||||||||||
Таблица 5.19. | При получении таблиц 5.17-5.19 действовали по стандартной схеме. Занятыми оказались, как и положено, 5 клеток (3+3-1=5), остается найти значение целевой функции для найденного опорного решения:
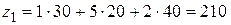
|
Проведем теперь построение начального опорного решения методом минимальной стоимости (таблицы 5.20-5.24).
Таблица 5.20. |
Таблица 5.21. | ||||||||||||||||||||||||||||||||
Таблица 5.22. |
Таблица 5.23. | ||||||||||||||||||||||||||||||||
Таблица 5.24. | Опять заняты 5 клеток, находим значение целевой функции для найденного опорного решения:
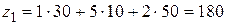 Замечание. При записи ответа (начального опорного решения) последние столбцы в таблицах 5.19 и 5.24 не учитываются.
Замечание. При записи ответа (начального опорного решения) последние столбцы в таблицах 5.19 и 5.24 не учитываются.
|
3. Проверка оптимальности решения. Метод потенциалов. Для проверки оптимальности решения введем потенциалы строк (ui, i=1,2,…,M) и столбцов (vj, j=1,2,…,N) – числа, которые определяются системой уравнений 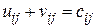 , составленных по занятым клеткам. Заметим, что занятых клеток M+N-1, поэтому мы имеем систему из M+N-1 уравнений с M+N неизвестными потенциалами. Это неопределенная система (см. [3, §6]), нас интересует любое частное решение, поэтому любому из потенциалов можно на первом шаге дать значение, равное нулю. Далее последовательно находятся все потенциалы, которые записываются в дополнительный правый столбец и в дополнительную нижнюю строку таблицы транспортной задачи (общую схему см. в таблице 5.25).
, составленных по занятым клеткам. Заметим, что занятых клеток M+N-1, поэтому мы имеем систему из M+N-1 уравнений с M+N неизвестными потенциалами. Это неопределенная система (см. [3, §6]), нас интересует любое частное решение, поэтому любому из потенциалов можно на первом шаге дать значение, равное нулю. Далее последовательно находятся все потенциалы, которые записываются в дополнительный правый столбец и в дополнительную нижнюю строку таблицы транспортной задачи (общую схему см. в таблице 5.25).
| B A | B1 | B2 | … | BM | Потенциалы строк |
| A1 | с11 | с12 | … | с1N | u1 |
| A2 | с21 | с22 | … | с2N | u2 |
| … | … | … | … | … | … |
| AM | сM1 | сM2 | cMN | uM | |
| Потенциалы столбцов | v1 | v2 | … | vN |
Таблица 5.25
После определения потенциалов находим оценки для свободных клеток по правилу 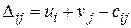 , записываем их в верхнюю часть каждой свободной клетки. Решение является оптимальным, если все найденные оценки неположительны (меньше или равны 0).
, записываем их в верхнюю часть каждой свободной клетки. Решение является оптимальным, если все найденные оценки неположительны (меньше или равны 0).
Пример. Проверить оптимальность решения, построенного в примере 5.4 (см. таблицу 5.24).
Решение. Сначала по таблице 5.24 определяем потенциалы.
Занятыми являются клетки (1;1), (2;1), (2;2), (2;3), (3;2). С учетом стоимостей, записанных в этих клетках, составляем систему уравнений
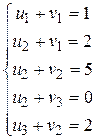
|
Таблица 5.26. |
Пусть 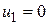 . Далее последовательно: из первого уравнения
. Далее последовательно: из первого уравнения 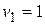 , из второго уравнения
, из второго уравнения 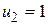 , из третьего
, из третьего 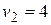 , из четвертого
, из четвертого 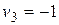 , из пятого
, из пятого 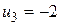 . Результаты собраны в таблице 5.26.
. Результаты собраны в таблице 5.26.
Расчет оценок проводится по формуле 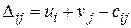 непосредственно в таблице 5.27, с учетом найденных выше потенциалов
непосредственно в таблице 5.27, с учетом найденных выше потенциалов
| В А | ui | |||
| 0+4-3=1>0 - | 0+(-1)-0=-1<0 - | |||
| -2+1-4=-5<0 - | -2+(-1)-0=-3<0 - | -2 | ||
| vj | -1 |
Таблица 5.27.
Итак, видно, что в ячейке (1;2) оценка положительна, т.е. предложенное решение не является оптимальным.
4. Оптимизация решения. Одним из основных понятий в этом пункте является цикл – последовательность клеток таблицы транспортной задачи, в которой две и только две соседние клетки расположены в одной строке или в одном столбце, причем первая и последняя клетки также находятся в одной строке или в одном столбце. Известно, что в таблице транспортной задачи, содержащей опорное решение, для любой свободной клетки можно построить единственный цикл, содержащий эту клетку и часть занятых.
Если решение не оптимальное, то среди положительных оценок выбираем наибольшую (в случае равенства наибольших оценок – выбираем ячейку с наименьшей стоимостью). Для выбранной ячейки строим цикл, включающий эту клетку и часть занятых клеток, причем свободная клетка получает знак «+», а далее знак чередуется. Для попавших в цикл ячеек определяем величину 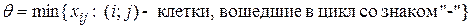 . Перемещаем перевозки по циклу в соответствии с правилом: в ячейках со знаком «+» q добавляется к значению xij, а в ячейках со знаком «-» q из xij вычитается. При этом клетка, в которой изначально находился объем перевозок, равный q, становится пустой, а свободная с выбранной «плохой» оценкой - занятой.
. Перемещаем перевозки по циклу в соответствии с правилом: в ячейках со знаком «+» q добавляется к значению xij, а в ячейках со знаком «-» q из xij вычитается. При этом клетка, в которой изначально находился объем перевозок, равный q, становится пустой, а свободная с выбранной «плохой» оценкой - занятой.
Замечание. Если минимальное значение q достигается в нескольких клетках, то только одна из них становится пустой, а в остальных объем перевозок выставляется равным 0; это позволяет сохранить необходимое количество занятых клеток.
После перемещения груза по циклу новое решение проверяется на оптимальность, и в случае необходимости процесс повторяется.
Пример. Найти оптимальное решение для транспортной задачи из примера 5.4.
Решение. Условия были приведены в таблице 5.14. Задача была открытой, поэтому сначала был введен фиктивный потребитель. Начальное опорное решение, построенное методом минимальной стоимости – в таблице 5.24. Таблица 5.27 (с потенциалами и оценками) свидетельствует, что построенное решение не оптимальное, а ячейка (1;2) – единственная ячейка с положительной оценкой. С нее и начнем строить цикл. По таблице 5.27 видно, что его образуют ячейки (1;2), (2;2), (2;1), (1;1). В силу сказанного выше ячейки
Таблица 5.2 8. | (1;2) и (2;1) будут иметь знак «+», ячейки (2;2) и (1;1) – знак «-». Объем перевозок в ячейке (2;2) равен 10, в ячейке (1;1) 30, минимальное значение q=10. Таким образом, в ячейках (1;2) и (2;1) объем перевозок будет увеличен на 10, а в ячейках (2;2) и (1;1) уменьшен на 10, при этом ячейка (2;2) освободится. Новое опорное решение приведено в таблице 5.28. |
Проверим оптимальность этого плана. По занятым клеткам составим систему уравнений для определения потенциалов и решим ее, полагая 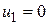 (читатель может проделать это самостоятельно). Затем запишем потенциалы (см. таблицу 5.29) и в этой же таблице высчитаем оценки свободных клеток.
(читатель может проделать это самостоятельно). Затем запишем потенциалы (см. таблицу 5.29) и в этой же таблице высчитаем оценки свободных клеток.
| В А | ui | |||
| 0+(-1)-0<0 - | ||||
| 1+3-5<0 - | ||||
| -1+1-4<0 - | -1+(-1)-0<0 - | -1 | ||
| vj | -1 |
Таблица 5.29.
Все оценки отрицательны, значит, найденное опорное решение является оптимальным. Для завершения решения отбрасываем столбец с фиктивным
Таблица 5.30. | потребителем, записываем итоговую таблицу 5.30, соответствующую исходному условию, и находим для построенного оптимального плана значение целевой функции:
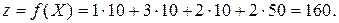 Заметим, что на втором складе осталось 10 единиц продукции, но это связано с тем, что задача была открытой.
Заметим, что на втором складе осталось 10 единиц продукции, но это связано с тем, что задача была открытой.
|
5. Алгоритм полного решения транспортной задачи. Подводя итог сказанному выше, определим порядок действий при решении транспортной задачи с M поставщиками и N потребителями.
1) Определить, является ли задача закрытой или открытой; в последнем случае ввести фиктивного потребителя или поставщика и построить новую таблицу.
2) Построить начальное опорное решение X1 (рекомендуется метод минимальной стоимости) и убедиться, что занято необходимое число клеток (M+N-1) – см. п.5.2.
3) Найти потенциалы с помощью занятых клеток из неопределенной системы 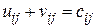 ((i;j) – адреса занятых клеток), а затем – оценки для свободных клеток
((i;j) – адреса занятых клеток), а затем – оценки для свободных клеток 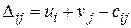 (здесь (i;j) – адреса свободных клеток) – см. п.5.3.
(здесь (i;j) – адреса свободных клеток) – см. п.5.3.
4) В случае, когда все оценки 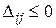 , опорный план является оптимальным, и остается найти значение целевой функции f(X1). Если же среди оценок
, опорный план является оптимальным, и остается найти значение целевой функции f(X1). Если же среди оценок 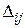 оказались положительные, то выбираем ячейку с наибольшей положительной оценкой, строим для нее цикл и переходим к новому опорному решению X2 – см. п. 5.4. При этом должно выполняться неравенство f(X2)£ f(X1). Затем возвращаемся к п. 3) алгоритма.
оказались положительные, то выбираем ячейку с наибольшей положительной оценкой, строим для нее цикл и переходим к новому опорному решению X2 – см. п. 5.4. При этом должно выполняться неравенство f(X2)£ f(X1). Затем возвращаемся к п. 3) алгоритма.
6. Транспортная задача с ограничениями. Значительное количество экономических задач (порой не имеющих ничего общего с транспортировкой грузов) могут быть сведены к модели транспортной задачи. При этом величины cij могут означать стоимость, расстояние, время, производительность (см., например, [4, раздел D, п.6.14]). В то же время в самой транспортной задаче возникают различные ограничения (например, по критерию времени, при наличии особо важного потребителя – в открытой задаче это означает, что его запросы должны быть удовлетворены полностью). Ниже для примера рассматривается ситуация, когда вводятся ограничения на пропускную способность. При этом необходимо учитывать следующие правила.
Правило 1 (для ограничения 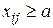 ). Перед решением задачи необходимо уменьшить запасы i -го поставщика и запросы j -го потребителя на величину a (резервируется перевозка
). Перед решением задачи необходимо уменьшить запасы i -го поставщика и запросы j -го потребителя на величину a (резервируется перевозка 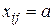 ). После решения задачи в оптимальном плане найденный объем перевозок
). После решения задачи в оптимальном плане найденный объем перевозок 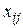 увеличивается на величину a.
увеличивается на величину a.
Правило 2 (для ограничения 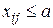 ). Перед решением задачи необходимо вместо j -го потребителя ввести двух потребителей. Первый, с номером j, будет иметь запрос a, второй, с номером N+1 (в таблицу добавляем новый, последний столбец) будет иметь запрос Bj-a. Стоимости в новом столбце совпадут с исходными за исключением i -й строки (в ней стоимость принимается равной сколь угодно большому положительному числу – это обеспечивает «не появление в ней перевозок»). После решения задачи в оптимальном плане объемы перевозок j -го и N+1 -го потребителей суммируются.
). Перед решением задачи необходимо вместо j -го потребителя ввести двух потребителей. Первый, с номером j, будет иметь запрос a, второй, с номером N+1 (в таблицу добавляем новый, последний столбец) будет иметь запрос Bj-a. Стоимости в новом столбце совпадут с исходными за исключением i -й строки (в ней стоимость принимается равной сколь угодно большому положительному числу – это обеспечивает «не появление в ней перевозок»). После решения задачи в оптимальном плане объемы перевозок j -го и N+1 -го потребителей суммируются.
Пример. Решить транспортную задачу с таблицей 5.31 и ограничениями: 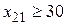 , , 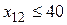
|
|
Решение. Задача изначально является закрытой (и запасы, и запросы равны 200). В соответствии со сказанным выше запасы во второй строке и запросы в первом столбце уменьшаются на 30 (учтено условие 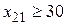 ). Далее во втором столбце запросы остаются равными 40, а мы достраиваем новый столбец с запросами 50-40=10. Стоимости в этом столбце совпадут с исходными, кроме ячейки в первой строке, куда запишем сколь угодно большое положительное число M. В результате нам нужно будет решать обычным способом (см. п. 5.5) транспортную задачу с таблицей 5.32. В таблице 5.33 приводится ее начальное опорное решение, найденное методом минимальной стоимости (читатель может провести построение сам).
). Далее во втором столбце запросы остаются равными 40, а мы достраиваем новый столбец с запросами 50-40=10. Стоимости в этом столбце совпадут с исходными, кроме ячейки в первой строке, куда запишем сколь угодно большое положительное число M. В результате нам нужно будет решать обычным способом (см. п. 5.5) транспортную задачу с таблицей 5.32. В таблице 5.33 приводится ее начальное опорное решение, найденное методом минимальной стоимости (читатель может провести построение сам).
Таблица 5.32 |
|
При нахождении потенциалов удобно считать, что 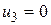 . Тогда оставшиеся значения быстро находятся из системы уравнений (по занятым клеткам)
. Тогда оставшиеся значения быстро находятся из системы уравнений (по занятым клеткам)
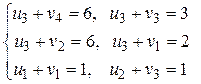
| В А | ui | ||||
| 6+(-1)-2=3>0 | 3+(-1)-4<0 | 6+(-1)-M<0 М | -1 | ||
| 2+(-2)-3<0 | 6+(-2)-5<0 | 6+(-2)-5<0 | -2 | ||
| vj |
Таблица 5.34
Результаты вычислений, а также расчет оценок в свободных клетках приведены в таблице 5.34. В ней в ячейке (1;2) находится положительная оценка, значит, решение не оптимальное. Цикл для перехода будем строить, начиная с этой ячейки (других «кандидатов» просто нет). В цикл войдут ячейки (1;2), (3;2), (3;1), (1;1). При этом у ячеек (1;2) и (3;1) знак «+», у ячеек (3;2) и (1;1) знак «-». Из значений в «отрицательных» ячейках (50 и 40) наименьшее 40, это и будет перемещаемый объем перевозок q.
| В таблице 5.35 приведен результат перемещения по циклу (новое опорное решение), ячейка (3;2) освободилась, но число занятых клеток сохранилось. Результат нахождения потенциалов (проверьте!) и расчет оценок находятся в таблице 5.36. |
|
| В А | ui | ||||
| 3+(-1)-4<0 | 6+(-1)-M<0 М | -1 | |||
| 2+(-2)-3<0 | 3+(-2)-5<0 | 6+(-2)-5<0 | -2 | ||
| 3+0-6<0 | |||||
| vj |
Таблица 5.36
| Итак, найденное решение оптимально (все оценки неположительны) – для задачи с таблицей 5.32. Теперь нужно вернуться к исходной задаче, в соответствии с правилами 1 и 2. Для этого объединим объемы перевозок из второго и четвертого столбца; запасы второй строки и запросы первого столбца увеличим на 30 (т.е. вернем в исходное состояние) и объем перевозок в ячейке (1;1) также увеличим на 30 (он был равен 0, поэтому получили 30). |
Таблица 5.37 |
Оптимальный план исходной задачи дан в таблице 5.37 (обратите внимание, что за счет объединения столбцов и появления ненулевого объема перевозок в ячейке (2;1) количество занятых клеток больше числа N+M-1, равного в данной задаче 3+3-1=5). Итак, остается найти оптимальное значение целевой функции: 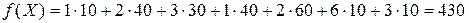 .
.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 514; Нарушение авторских прав?; Мы поможем в написании вашей работы!