Системы дифференциальных уравнений

Определение: система дифференциальных уравнений вида

где 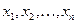- неизвестные функции независимой переменной 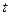, называется нормальной системой.

Если правые части нормальной системы дифференциальных уравнений являются линейными функциями относительно 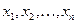, то система дифференциальных уравнений называется линейной.

1) Иногда нормальную систему дифференциальных уравнений удается свести к одному уравнению - го порядка, содержащему одну неизвестную функцию. Сведение нормальной системы к одному уравнению может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одного.

В некоторых случаях, комбинируя уравнения системы, после несложных преобразований удается получить легко интегрируемые уравнения, что позволяет найти решение системы.

2) Пусть дана система 3 линейных дифференциальных уравнений с 3 неизвестными функциями, коэффициенты которых постоянные:

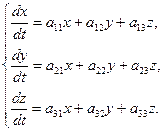
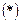
Общее решение имеет вид: .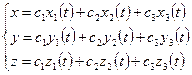

Здесь 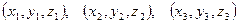- нетривиальные частные решения системы, причем такие, что каждая тройка функций образуют ФСР .

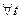Ищем такие частные решения системы в виде , здесь - некоторые константы. Подставив значения в систему дифференциальных уравнений 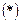, получим систему линейный алгебраических уравнений относительно :

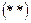
Составляем характеристическое уравнение:

.

Оно имеет три корня: действительных или комплексно-сопряженных.

- Если корни действительные и различные 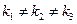, то для каждого корня находим из системы 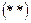одно из ее решений вида:

Линейная комбинация полученных частных решений определит общее решение заданной системы.

- Если среди корней есть пара комплексно-сопряженных чисел, т.е. 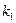- действительное, 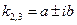, то аналогичным способом с помощью корня 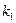находим первое частное решение системы в действительной форме. С помощью корня 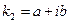или получаем новое частное решение в комплексной форме. Выделив в новом решении действительные и мнимые части, составляем из них соответственно частные решения в действительной форме.

РАЗДЕЛ II. ТЕОРИЯ ПОЛЯ

2.1. Скалярное поле и его характеристики:

Определение: все пространство или любая его часть, в каждой точке которой задана некоторая скалярная величина , называется скалярным полем.

Характеристики скалярного поля:

1 ) Поверхности уровня: 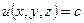; линии уровня: .

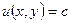2) Производная по направлению.

Формула нахождения: , где - углы,

Образованные направлением дифференцирования 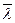с соответствующими координатными осями.

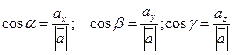
Производная характеризует скорость изменения функции поля в заданном направлении.

3) Градиент:

Формула нахождения: ;

Свойства градиента:

- направлен по нормали к поверхности уровня;

- определяет направление, по которому достигает наибольшего значения и, следовательно, функция поля растет быстрее всего.

2.2. Векторное поле и его характеристики:

Определение: все пространство или любая его часть, в каждой точке которой задана некоторая векторная физическая величина , называется векторным полем.

Векторное поле считается заданным, если задан вектор .

Характеристики векторного поля

1) Векторные линии:

- система дифференциальных уравнений векторных линий;

2) Поток:

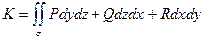
и в частности:

;

В поле скоростей текущей жидкости поток вектора поля через поверхность определяет количество жидкости, протекающей через эту поверхность в единицу времени – физический смысл потока через незамкнутую поверхность.

В поле скоростей текущей жидкости поток вектора поля изнутри поверхности определяет разность между количеством жидкости вытекающей и втекающей в область 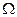в единицу времени - физический смысл потока через замкнутую поверхность.

3) Дивергенция: .

Если , то поле называется соленоидальным.

Физический смысл дивергенции:

В поле скоростей текущей жидкости дивергенция векторного поля в точке характеризует мощность источника или стока, находящегося в этой точке.

4) Циркуляция: , также по формуле:

.

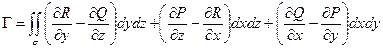Физический смысл: циркуляция силового поля вдоль замкнутого контура, помещенного в поле, выражает работу этого поля при перемещении материальной точки вдоль замкнутого контура.

5) Ротор: .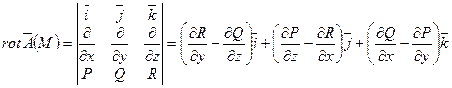

Физический смысл: в поле скоростей вращающейся жидкости ротор поля с точностью до числового множителя равен угловой скорости.

Если 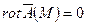, то поле потенциальное.

Потенциал находим по формуле:

, здесь - координаты произвольной фиксированной точки поля, 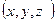- координаты переменной точки поля.

Если 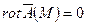, , то поле называется гармоническим.

РАЗДЕЛ III. РЯДЫ

3.1. Основные понятия:

Определение: выражение вида 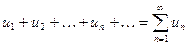называется бесконечным числовым рядом.

Признаки числового ряда: наличие при суммировании бесчисленного множества членов и наличие закона изменения членов ряда.

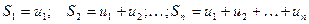- частичные суммы.

Определение: ряд 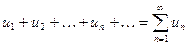называется сходящимся при , если существует конечный предел его частичных сумм и расходящимся, если такой предел не существует.

Конечный предел частичных сумм называется суммой ряда.

Теорема (необходимый признак сходимости):

Если ряд сходится, то его общий член стремится к нулю при неограниченном увеличении порядкового номера, т.е. .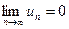

Теорема (достаточный признак расходимости):

Если общий член ряда не стремится к нулю, то ряд расходится, т.е. если 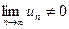, то ряд 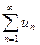- расходится.

3.2. Знакопостоянные ряды:

Определение: ряд, все члены которого или только положительные, или только отрицательные, называется знакопостоянным.

Дата добавления: 2015-06-28