Уравнения переходных процессов в цепях с распределенными параметрами

Переходные процессы в цепях с распределенными параметрами

Переходные процессы в цепях с распределенными параметрами имеют характер блуждающих волн, распространяющихся по цепи в различных направлениях. Эти волны могут претерпевать многократные отражения от стыков различных линий, от узловых точек включения нагрузки и т.д. В результате наложения этих волн картина процессов в цепи может оказаться достаточно сложной. При этом могут возникнуть сверхтоки и перенапряжения, опасные для оборудования.

Переходные процессы в цепях с распределенными параметрами возникают при различных изменениях режимов их работы: включении-отключении нагрузки, источников энергии, подключении новых участков линии и т.д. Причиной переходных процессов в длинных линиях могут служить грозовые разряды.

При рассмотрении схемы замещения цепи с распределенными параметрами были получены дифференциальные уравнения в частных производных

;

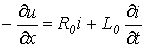(5)

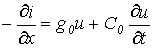
(6)

Их интегрирование с учетом потерь представляет собой достаточно сложную задачу. В этой связи будем считать цепь линией без потерь, т.е. положим 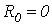и 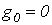. Такое допущение возможно для линий с малыми потерями, а также при анализе начальных стадий переходных процессов, часто наиболее значимых в отношении перенапряжений и сверхтоков.

С учетом указанного от соотношений (5) и (6) переходим к уравнениям

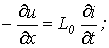
(7)

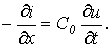
(8)

Для получения уравнения (7) относительно одной переменной продифференцируем (7) по х, а (8) – по t:

;

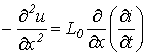(9)

.

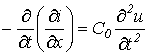(10)

Учитывая, что для линии без потерь 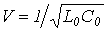, после подстановки соотношения (10) в (9) получим

.

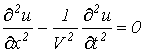(11)

Аналогично получается уравнение для тока

.

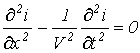(12)

Волновым уравнениям (11) и (12) удовлетворяют решения

;

.

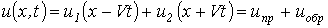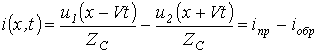Как и ранее, прямые и обратные волны напряжения и тока связаны между собой законом Ома для волн

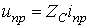и ,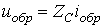

где .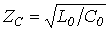

При расчете переходных процессов следует помнить:

1. В любой момент времени напряжение и ток в любой точке линии рассматриваются как результат наложения прямой и обратной волн этих переменных на соответствующие величины предшествующего режима.
2. Всякое изменение режима работы цепи с распределенными параметрами обусловливает появление новых волн, накладываемых на существующий режим.
3. Для каждой волны в отдельности выполняется закон Ома для волн.

Как указывалось, переходный процесс в цепях с распределенными параметрами характеризуется наложением многократно отраженных волн. Рассмотрим многократные отражения для двух наиболее характерных случаев: подключение источника постоянного напряжения к разомкнутой и короткозамкнутой линии.

Дата добавления: 2014-01-03